 |
Зависимость подачи жидкости от расхода газа
|
|
|
|
ОСНОВЫ ТЕОРИИ ПОДЪЕМА ЖИДКОСТИ В СКВАЖИНЕ
Подъем жидкости из скважин нефтяных месторождений практически всегда сопровождается выделением газа. Поэтому для понимания процессов подъема жидкости из скважин, умения проектировать установки для подъема и выбирать необходимое оборудование, надо знать законы движения газожидкостных смесей (ГЖС) в трубах. При всех известных способах добычи нефти приходится иметь дело с движением газожидкостных смесей либо на всем пути от забоя до устья, либо на большей части этого пути. Эти законы сложнее законов движения однородных жидкостей в трубах и изучены хуже. Если при движении однофазного потока приходится иметь дело с одним опытным коэффициентом λ (коэффициент трения), то при движении двухфазного потока - газожидкостных смесей приходится прибегать по меньшей мере к двум опытным характеристикам потока, которые в свою очередь зависят от многих других параметров процесса и условий движения, многообразие которых чрезвычайно велико.
Физика процесса движения газожидкостной смеси в вертикальной трубе
Зависимость подачи жидкости от расхода газа
Качественную характеристику процесса движения газожидкостной смеси (ГЖС) в вертикальной трубе легче уяснить из следующего простого опыта (рис. 7.1). Представим, что трубка 1 длиною L погружена под уровень жидкости неограниченного водоема на глубину h. К нижнему открытому концу трубки, который по аналогии с промысловой терминологией будем называть башмаком, подведена другая трубка 2 для подачи с поверхности сжатого газа. На трубке имеется регулятор расхода 3, с помощью которого можно установить желаемый расход газа.
|
|
|
Рис. 7.1. Принципиальная схема газожидкостного подъемника
Давление у башмака подъемной трубки 1 будет равно гидростатическому на глубине h - P1 = rgh и, очевидно, не будет изменяться от того, много или мало газа подается к башмаку. По трубке 2 подается газ, и в трубке 1 создается газожидкостная смесь средней плотности rс, которая поднимается на некоторую высоту H. Поскольку внутренняя полость трубки 1 и наружная область являются сообщающимися сосудами, имеющими на уровне башмака одинаковые давления, то можно написать равенство
откуда
. (7.1)
Плотность смеси в трубке rс зависит от расхода газа V. Чем больше V, тем меньше rс. Изменяя V, можно регулировать Н. При некотором расходе V = V1 величина Н может достигнуть L. При V<V1 H<L. При V>V1 H>L и наступит перелив жидкости через верхний конец трубки 1. При дальнейшем увеличении V расход поступающей на поверхность жидкости q увеличится. Однако при непрерывном увеличении V расход жидкости не будет увеличиваться непрерывно, так как под воздействием неизменяющегося перепада давления DР = Р1 - Р2 (Р1 = const, так как h = const), труба определенной длины L и диаметра d должна пропускать конечное количество жидкости, газа или газожидкостной смеси. Таким образом, при некотором расходе газа V=V2 дебит достигнет максимума q = q max.
Можно представить другой крайний случай, когда к башмаку подъемной трубы подводится так много газа, что при постоянном перепаде давления DР = Р1 - Р будет идти только газ, DР будет расходоваться на преодоление всех сопротивлений, вызванных движением по трубе чистого газа. Расход этого газа пусть будет V=V3. Если к башмаку подать еще больший расход (V>V3), то излишек газа не сможет пройти через подъемную трубу, так как ее пропускная способность при данных условиях (L, d, DP) равна только V3, и устремится мимо трубы, оттесняя от башмака жидкость. Очевидно, при этом расход жидкости будет равен нулю (q = 0). Таким образом, из этого опыта можно сделать следующий вывод.
|
|
|
1. При V<V1 q = 0 (H < L).
2. При V = V1 q = 0 (H = L) (начало подачи).
3. V1 < V < V2 0 < q < qmax (H > L),
4. При V = V2 q = qmax (точка максимальной подачи).
5. При V2 < V < V 3 qmax > q > 0.
6. При V = V3 q = 0 (точка срыва подачи).
Обычно правая ветвь кривой q(V) (рис. 7.2) пологая, левая крутая.
Рис. 7.2. Зависимость подачи q газожидкостного подъемника от расхода газа V
Для всех точек кривой постоянным является давление P1, так как погружение h в процессе опыта не изменялось. Существует понятие - относительное погружение e = h / L. Таким образом, для данной кривой ее параметром будет величина относительного погружения ε.
7.1.2. Зависимость положения кривых q (V) от погружения
Поскольку при наших рассуждениях никаких ограничений на величину e не накладывалось, то при любых e, лежащих в пределах 0 < e < 1, вид соответствующих кривых q(V) будет одинаковый. При увеличении е новые кривые q(V) обогнут прежнюю, так как с ростом h потребуется меньший расход газа для наступления перелива. По тем же причинам возрастет qmax, а точка срыва подачи на соответствующих кривых сместится вправо. При уменьшении e все произойдет наоборот. Новые кривые q(V) расположатся внутри прежних и при e = 0 кривая q(V) выродится в точку. Другой предельный случай - e = 1 (h = L, 100% погружения). В этом случае при бесконечно малом расходе газа немедленно произойдет перелив. Точка начала подачи сместится в начало координат. Кривая q(V) для e = 1 начнется в начале координат и обогнет все семейство кривых. Таким образом, каждый газожидкостный подъемник характеризуется семейством кривых q(V), каждая из которых будет иметь свой параметр e (рис. 7.3).
Рис. 7.3. Семейство кривых q(V) для газожидкостного подъемника данного диаметра
7.1.3. Зависимость положения кривых q(V) от диаметра трубы
В наших рассуждениях никаких ограничений на диаметр подъемной трубы и на ее длину не накладывается. Поэтому аналогичное семейство кривых q(V) должно существовать для подъемников любого диаметра и любой длины. Однако возникает вопрос, как располагать повое семейство кривых для трубы диаметром d2 > d1 по отношению к прежним кривым. Увеличение диаметра потребует большого расхода газа, так как
Рис. 7.4. Семейство кривых q(V) для двух газожидкостных подъемников различных диаметров
|
|
|
объем жидкости, который необходимо разгазировать для достижения данной величины rс, при прочих равных условиях (h = const, L = const) возрастает пропорционально d2. Пропускная способность трубы по жидкости, газу или газожидкостной смеси (ГЖС) также возрастет. Поэтому для увеличенного диаметра будет существовать также семейство кривых q(V), все точки которого будут смещены вправо, в сторону увеличенных объемов, кроме одной точки, совпадающей с началом координат для кривой q(V) при e = 1. В каждом из этих семейств и любых других, кривые q(V) при значениях e, близких к единице и к нулю, не имеют практического значения, так как они либо неосуществимы (e = 0), либо бессмысленны (e = 1), и введены в рассуждения только для понимания физики процессов, происходящих при движении ГЖС в трубах.
7.1.4. К. п. д. процесса движения ГЖС
На каждой кривой q(V) имеется еще одна характерная и очень важная точка, точка так называемой оптимальной производительности, соответствующая наибольшему к. п. д. Если проанализировать произвольную кривую q(V), для которой e = const, то для нее будут справедливы следующие рассуждения.
Из определения понятия к. п. д. следует, что
. (7.2)
Полезная работа заключается в поднятии жидкости с расходом q на высоту L - h, так что
. (7.3)
Затраченная работа - это работа газа, расход которого, приведенный к стандартным условиям, равен V. Полагая для простоты, что процесс расширения газа изотермический, на основании законов термодинамики идеальных газов можем записать
, (7.4)
где Р1 + Рo - абсолютное давление у башмака; Р2 + Ро - то же на устье, Ро - атмосферное давление.
Подставляя (7.3) и (7.4) в (7.2), получим
. (7.5)
В (7.5) все величины, кроме q и V, постоянны, так как рассматривается одна кривая q(V), для которой ε = const. Следовательно, для данной кривой
, (7.6)
где С - константа.
Поэтому к. п. д. будет иметь максимальное значение в той точке, в которой отношение q / V максимально. Но q / V = tg φ, так как q - ордината, V - абсцисса, φ - угол наклона прямой, проведенной из начала координат через данную точку (q, V). Только для касательной tgφ будет иметь максимальное значение, так как только для нее угол φ максимален. Поэтому в точке касания прямой, проведенной из начала координат с кривой q(V), получаются такой дебит q и такой расход газа V, при которых к. п. д. процесса будет наибольшим. Расход q при максимальном к. п. д. называют оптимальным дебитом qoпт.
|
|
|
Таким образом, для любой кривой q(V), имеющей ε = const, оптимальный расход жидкости определится как точка касания касательной, проведенной из начала координат.
7.1.5. Понятие об удельном расходе газа
Удельным расходом газа называют отношение
. (7.7)
Из определения следует, что для точек начала и срыва подачи, когда q = 0, а V > 0, удельный расход R обращается в бесконечность. Для режима оптимальной подачи, когда к. п. д. максимален, R минимально. Это очевидно, так как при максимальном
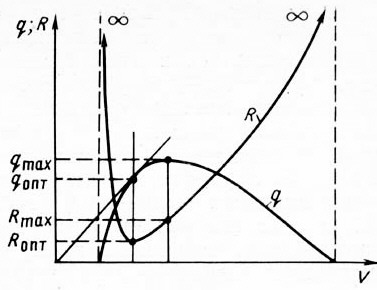
Рис. 7.5. Зависимость удельного расхода газа R от общего расхода газа V для данной кривой q (V)
к. п. д. должно расходоваться минимально возможное количество газа на подъем единицы объема жидкости. При режиме максимальной подачи (qmax) η < ηmax. Поэтому и удельный расход газа R будет при этом режиме больше оптимального. Величина R может быть получена для любой точки кривой q(V) путем деления абсциссы на ординату данной точки (рис. 7.5).
7.1.6. Зависимость оптимальной и максимальной подач от относительного погружения
Для любого семейства кривых q(V), построенного для данного диаметра труб, можно найти qmax и qопт и проследить их зависимость от изменения относительного погружения ε. С увеличением ε величины qmax также увеличиваются по криволинейному закону (см. рис. 7.3 и 7.4). Что касается qопт, то последние, во-первых, всегда остаются меньше соответствующих qmax и, во-вторых, сначала увеличиваются с ростом ε, а затем при 0,5 < ε < 1 начинают уменьшаться. В частности, при ε = 1 кривая q(V) выходит из начала координат. Поэтому касательная, проведенная из начала координат, будет иметь точку соприкосновения с кривой q(V) в начале координат. Это
Рис. 7.6. Зависимость оптимальной qопт и максимальной qmax подачи от относительного нагруження ε
означает для q(V) при ε = 1 qопт = 0. Таким образом, величины qопт должны сначала увеличиваться, затем уменьшаться и при ε = 1 обращаться в нуль. Наибольшая величина qопт достигается при ε = 0,5 - 0,6 (рис. 7.6). Это подтверждается и многочисленными опытами различных исследователей. Отсюда можно сделать важный для практики вывод: для достижения наибольшей эффективности работы газожидкостного подъемника необходимо осуществить погружение подъемной трубы под уровень жидкости на 50 - 60% (ε = 0,5 - 0,6) от всей длины трубы L. Однако эта рекомендация в реальных условиях не всегда может быть выполнена из-за низкого динамического уровня или из-за ограниченного давления газа, используемого для этой цели.
|
|
|
Рис. 7.7. Структуры газожидкостного потока: а - эмульсионная; б - четочная; в – стержневая
7.1.7. Структура потока ГЖС в вертикальной трубе
В зависимости от физических свойств жидкости и характера ввода газа в поток могут возникать различные структуры движения ГЖС в трубе, которые существенным образом влияют на энергетические показатели подъема жидкости. В фонтанных скважинах на участке НКТ, где давление меньше давления насыщения, выделяющийся из нефти свободный газ образует тонкодисперсную структуру, называемую эмульсионной. Мелкие газовые пузырьки более или менее равномерно пронизывают массу нефти, образуя практически однородную квазигомогенную смесь газа и жидкости. Вследствие своей малости (доли мм) и большой плотности газовые пузырьки обладают малой архимедовой силой. Поэтому их скорость всплытия относительно жидкости пренебрежимо мала и в расчетах может не учитываться. Это происходит до тех пор, пока в результате уменьшения давления при движении смеси вверх по трубе газовые пузырьки, расширяясь, увеличивают объемное газосодержание потока до 20 - 25%. При дальнейшем уменьшении давления и поступлении из нефти новых количеств газа пузырьки, сливаясь, образуют глобулы больших размеров, измеряемые в диаметре несколькими сантиметрами. Скорость всплытия таких глобул в результате действия архимедовой силы становится большой, достигая нескольких десятков сантиметров в секунду. Это ухудшает энергетические показатели процесса подъема. Такая структура называется четочной.
При больших расходах газа возникает стержневая структура, при которой газ с распыленными в нем каплями жидкости движется непрерывным потоком, увлекая за собой по стенкам трубы волнистую пленку жидкости. При стержневой структуре движения скорость газа по отношению к жидкости достигает нескольких метров в секунду. Между эмульсионной, четочной и стержневой структурами не существует резких границ перехода и тем не менее некоторые исследователи выделяют и переходные структуры от эмульсионной к четочной, и от четочной к стержневой (рис. 7.7). На возникновение той или иной структуры существенное влияние оказывает вязкость нефти, а также наличие в ней различных ПАВ, способствующих диспергации газа в потоке.
7.2. Уравнение баланса давлений
При проектировании или анализе работы установок для подъема жидкости из скважин, когда по НКТ движется ГЖС, основным вопросом является определение потерь давления, связанных с этим движением. Рассматривая некоторый участок вертикальной трубы, в которой движется ГЖС, можно записать
, (7.8)
где Р1 - давление в нижней части трубы, Рс - давление, уравновешивающее гидростатическое давление столба ГЖС, Ртр - потери давления на преодоление сил трения при движении ГЖС, Рус - потери давления на создание ускорения потока ГЖС, так как его скорость при движении в сторону меньших давлений увеличивается из-за расширения газа; Р2 - противодавление на верхнем конце трубы.
Уравнение (7.8) справедливо для всех случаев: короткой и длинной трубы, вертикальной и наклонной и является основным при расчете потерь давления и их составляющих.
При практических расчетах могут возникнуть две основные задачи, когда известно давление вверху Р2 и требуется определить давление внизу Р1 или наоборот. При этом все другие условия, такие как длина трубы, ее диаметр, расход поднимаемой жидкости, свойства жидкости и газа и другие, должны быть известны. Это так называемые прямые задачи. Но могут возникать и другие задачи, которые можно назвать обратными, когда, например, требуется определить расход поднимаемой жидкости q при заданном перепаде давления Р1 - Р2. Или определить необходимое количество газа Го для подъема заданного количества жидкости q при заданном перепаде давления Р1 - Р2 и ряд других задач. Во всех случаях необходимо знать слагаемые, входящие в уравнение баланса давления (7.8).
Обозначим ρ - плотность жидкости, L - длина трубы по вертикали, ρс - плотность ГЖС, h - потеря напора на трение на участке трубы длиной в 1 м столба ГЖС, hус - потеря напора на ускорение на участке трубы длиной в 1 м столба ГЖС.
Тогда
. (7.9)
Деля все слагаемые на ρgL, найдем
. (7.10)
Слева от знака равенства написана величина, которая является действующим перепадом (Р1 - Р2), выраженным в метрах столба поднимаемой жидкости, отнесенным к 1 м длины трубы. Эту величину обозначают
. (7.11)
При Р2 = 0 (истечение в атмосферу) величина ε совпадает с тем относительным погружением (ε = h / L), о котором шла речь при рассмотрении физической характеристики процесса движения ГЖС.
Выражение (7.11) является более общим, так как учитывает противодавление P2. Уравнение (7.9) может быть записано в дифференциальной форме при L → 0
. (7.12)
или в конечных разностях
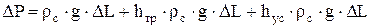. (7.13)
Величины ρc, hтр, hyc зависят от термодинамических условий потока, изменяющихся с глубиной, и в первую очередь существенно зависят от давления. Эти условия непрерывно изменяются вдоль трубы и их аналитический учет достаточно сложен. Задача сводится к интегрированию уравнения (7.12) в пределах от 0 до L, либо к численному суммированию приращений давления, определяемых (7.13), также в пределах от 0 до L. Чем меньше участки трубы ΔL, на которые может быть разбита вся длина подъемных труб, тем меньше будут изменяться слагаемые, входящие в уравнение баланса давления.
Если для таких коротких участков трубы рассчитать падение давления ΔPi, то общий перепад составит сумму
. (7.14)
где
. (7.15)
Из (7.14) следует, что если известно давление вверху Р2, то
. (7.16)
Если известно давление внизу P1, то
. (7.17)
Таким образом, задача сводится к расчету потерь давления на коротких участках подъемника при заданных параметрах движения (q, d, Г, ρ и пр.) и последующем их суммировании. Очевидно, чем больше n, т. е. чем меньше ΔL, тем точнее будет такое решение. Однако практика подобных вычислений показывает, что при n = 10 - 15 достигается достаточная точность.
7.3. Плотность газожидкостной смеси
Через данное сечение трубы при движении по ней ГЖС проходит некоторое количество газа и жидкости. Можно представить, что все газовые пузырьки занимают в сечении трубы суммарную площадь fг, а жидкость - остающуюся площадь в том же сечении fж, так что
,
где f - площадь сечения трубы (рис. 7.8). Плотность ГЖС в таком случае определится как средневзвешенная
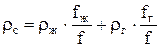, (7.18)
где ρж и ρг - плотность жидкости и газа при термодинамических условиях сечения.
Обычно fг / f обозначают через φ. Тогда fж / f = 1 - φ,
. (7.19)
Величина φ = fг / f называется истинным газосодержанием потока.
Обозначим V - объемный расход газа через данное сечение; q - объемный расход жидкости через то же сечение; Сг - линейная скорость движения газа относительно стенки трубы; Сж - линейная скорость движения жидкости относительно стенки трубы.
Тогда можно записать следующие соотношения:
. (7.20)
и
. (7.21)
Подставляя (7.20) и (7.21) в (7.18) и делая некоторые сокращения, получим
, (7.22)
В восходящем потоке газ движется быстрее жидкости, так как на него действует архимедова сила выталкивания. Обозначим
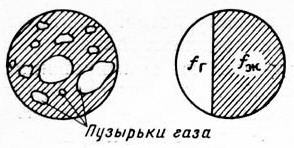
Рис. 7.8. Среднестатистические площади в трубе, занятые газом и жидкостью
, (7.23)
. (7.24)
Разделив числитель и знаменатель в (7.22) на q и вводя новые обозначения согласно (7.23) и (7.24), получим
, (7.25)
где r - газовый фактор, приведенный к термодинамическим условиям рассматриваемого сечения.
При Сг = Сж b = 1 и из (7.25) следует
. (7.26)
Этот случай соответствует идеальным условиям, при которых образуется идеальная смесь плотностью ρи. Относительная скорость газа (по отношению к жидкости)
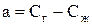, (7.27)
или
. (7.28)
Подставляя (7.28) в (7.23), получим
, (7.29)
Поскольку а > 0, то b > 1. Увеличение скорости газа при неизменном объемном расходе V уменьшает fг, следовательно, увеличивает fж. В результате плотность смеси, как это следует из (7.18) и (7.19), увеличивается. Таким образом, явление скольжения газа (a > 0) при неизменных объемных расходах q и V приводит к утяжелению смеси по сравнению с идеальным случаем. Поэтому чем больше а, тем больше потребуется давление на забое для поднятия данного количества жидкости.
Плотность реальной смеси
, (7.30)
где Δρ - увеличение плотности смеси, обусловленное скольжением. Для определения Δρ к (7.25) прибавим и отнимем ρи согласно (7.26), получим
Группируя слагаемые и делая некоторые преобразования, имеем
или после приведения к общему знаменателю в квадратных скобках и группировки слагаемых найдем
. (7.31)
Из сопоставления (7.31), (7.30) и (7.26) следует
. (7.32)
При b = 1 (отсутствие скольжения газа Сг = Сж) числитель в (7.32) обращается в нуль и Δρ = 0. Утяжеление ГЖС не происходит. С увеличением b (b > 1) Δρ монотонно увеличивается (рис. 7.9). Заштрихованная часть графика показывает увеличение плотности ГЖС за счет скольжения газа.
Из формулы (7.29) видно, что при одной и той же относительной скорости газа (a = const) b уменьшается при увеличении Сж, т. е. расхода жидкости. Отсюда следует важный для практики вывод - переход на трубы малого диаметра при определенных условиях за счет увеличения Сж уменьшит величину b, а это в свою очередь повлечет уменьшение Δρ.
Pиc. 7.9. Изменение плотности ГЖС в результате скольжения газа
Поэтому подъем ГЖС может быть осуществлен при меньшем давлении в нижней части трубы (при меньшем забойном давлении). Однако целесообразность перехода на трубы меньшего диаметра должна быть проверена расчетом, так как при этом возрастут потери давления на трение.
В теории движения ГЖС существуют важные понятия, через которые определяется плотность смеси. Это расходное газосодержание β и истинное газосодержание φ. Расходное газосодержание потока ГЖС определяется как отношение объемного расхода газа V к общему расходу смеси V+q:
. (7.33)
Истинное газосодержание потока ГЖС учитывает скольжение газа и поэтому является отношением площади, занятой газом fг, ко всему сечению трубы f:
. (7.34)
Тогда
. (7.35)
Из сопоставления (7.35) и (7.25) следует
. (7.36)
. (7.37)
Разделив в (7.33) числитель и знаменатель на q и используя обозначение (7.24), получим
. (7.38)
Отнимая в (7.38) по единице и меняя знак, получим
. (7.39)
или
. (7.39)
Сопоставляя (7.39), (7.38) и (7.26), видим, что
. (7.40)
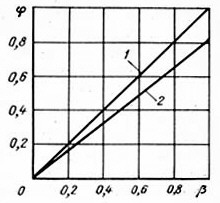
Рис. 7. 10. Зависимость φ от β при отсутствии скольжения газа
(β = φ, линия 1) и при скольжении (φ < β, линия 2)
Таким образом, плотность идеальной смеси (7.40) определяется расходным газосодержанием β, а плотность реальной смеси (7.35) - истинным φ.
Найдем формулы связи между φ, β, b и r. Из (7.37) и (7.38) имеем
,
откуда
. (7.41)
Решая (7.38) относительно г, найдем
. (7.42)
Подставляя (7.42) в (7.41), получим
.
Откуда после преобразований
. (7.43)
Решая (7.43) относительно b, получим
. (7.44)
При движении ГЖС возможны два предельных случая, когда по трубе движется одна жидкость fг = 0, следовательно, φ также равно нулю, и когда по трубе движется один газ fж = 0. Аналогично и для расходного газосодержания β. Поэтому физически возможными пределами изменениями φ и β будут 0 < φ <1, 0< β < 1. При отсутствии скольжения газа относительная его скорость равна нулю (а = 0), следовательно, Сг = Сж, b = 1 и из формулы (7.43) φ = β.
Таким образом, φ(β) для идеального подъемника будет являться прямой в виде диагонали квадрата линия 1 (рис.7.10).
Во всех других случаях при b > 1, т. е. при а > 0 (Сг > Сж), получим φ = β.
На диаграмме φ(β) линия 2 проходит ниже диагонали. Чем больше скольжение, т. е. чем больше а, а следовательно, и b, тем ниже пройдет линия φ(β).
Относительная скорость газа а зависит от следующих факторов: дисперсности газовых пузырьков, а следовательно, структуры движения ГЖС; вязкости жидкой фазы; разности плотностей газа и жидкости, от которой зависит подъемная сила; диаметра трубы и газонасыщенности потока ГЖС.
Попытки теоретического определения величины а не дают надежных результатов. Поэтому оценка относительной скорости газа проводится главным образом экспериментально и составляет основной предмет исследований. По некоторым рекомендациям предлагается принять φ = 0,833·β во всем диапазоне значений β представляющем практический интерес. Величина β всегда известна, так как расходами V и q либо задаются, либо вычисляют для заданных термодинамических условий.
7.4. Формулы перехода
В литературе по вопросам движения ГЖС для вычисления рс различные авторы используют различные выражения и различные подходы к определению этой важной величины. Покажем, что все возможное разнообразие подходов к определению ρс может быть осуществлено с помощью формул перехода, связывающих основные величины, определяющие ρс, такие как β, φ, r, b, а, C, Cж, Сг.
Ранее были получены следующие выражения:
, (7.45)
, (7.46)
. (7.47)
где
. (7.48)
. (7.49)
Из сопоставления (7.45) и (7.47) следует
. (7.50)
Так как при отсутствии скольжения Сг = Сж, b = 1. Из сопоставления (7.45) и (7.48) получим
. (7.51)
Используя (7.50) и (7.51) и подставляя их в (7.49), получим
. (7.52)
Решая (7.50) относительно r, найдем
. (7.53)
Решая (7.51) относительно r, найдем
. (7.54)
Приравнивая (7.53) и (7.54) и решая относительно b, найдем
. (7.55)
Решая (7.55) относительно φ, найдем
. (7.56)
При необходимости вычислить φ через относительную скорость газа а такое вычисление может быть сделано следующим образом. Имеем
. (7.57)
Формулу (7.57) можно выразить через β
. (7.58)
При определении ρс через величину b необходимо знать действительную скорость жидкости Сж и относительную скорость газа а. Можно легко вывести формулу для Сж
. (7.59)
Здесь С - приведенная скорость жидкости, равная q / f.
Увеличение плотности смеси Δρ можно выразить через φ и β следующим образом:
. (7.60)
Таким образом, используя формулы перехода, всегда можно перейти от одних величин, определяющих истинную плотность смеси, таких как φ или b, к другим величинам, таким как а, Сж и пр.
8. ЭКСПЛУАТАЦИЯ ФОНТАННЫХ СКВАЖИН
Фонтанирование скважин обычно происходит на вновь открытых месторождениях нефти, когда запас пластовой энергии велик, т. е. давление на забоях скважин достаточно большое, чтобы преодолеть гидростатическое давление столба жидкости в скважине, противодавление на устье и давление, расходуемое на преодоление трения, связанное с движением этой жидкости.
Общим обязательным условием для работы любой фонтанирующей скважины будет следующее основное равенство:
, (8.1)
где Рс - давление на забое скважины; Рг, Ртр, Ру - гидростатическое давление столба жидкости в скважине, рассчитанное по вертикали, потери давления на трение в НКТ и противодавление на устье, соответственно.
Различают два вида фонтанирования скважин:
фонтанирование жидкости, не содержащей пузырьков газа, - артезианское фонтанирование;
фонтанирование жидкости, содержащей пузырьки газа, облегчающего фонтанирование, - наиболее распространенный способ фонтанирования.
Артезианский способ встречается при добыче нефти редко. Он возможен при полном отсутствии растворенного газа в нефти и при забойном давлении, превышающем гидростатическое давление столба негазированной жидкости в скважине. При наличии растворенного газа в жидкости, который не выделяется благодаря давлению на устье, превышающему давление насыщения, и при давлении на забое, превышающем сумму двух давлений: гидростатического столба негазированной жидкости и давления на устье скважины.
Поскольку присутствие пузырьков свободного газа в жидкости уменьшает плотность последней и, следовательно, гидростатическое давление такого столба жидкости, то давление на забое скважины, необходимое для фонтанирования газированной жидкости, существенно меньше, чем при артезианском фонтанировании.
8.1. Артезианское фонтанирование
Теоретическое описание процесса артезианского фонтанирования практически не отличается от расчета движения однородной жидкости по трубе. Давление на забое скважины Рс при фонтанировании определяется уравнением (8.1), в котором гидростатическое давление столба жидкости благодаря постоянству плотности жидкости определяются простым соотношением
, (8.2)
где ρ - средняя плотность жидкости в скважине; Н - расстояние по вертикали между забоем (обычно серединой интервала перфорации) и устьем скважины.
Для наклонных скважин
,
где L - расстояние от забоя до устья вдоль оси наклонной скважины; α - средний зенитный угол кривизны скважины. Для наклонных скважин, имеющих на разных глубинах различный угол кривизны αi, расстояние Н необходимо определять разделением глубины скважины на интервалы и суммированием проекций этих интервалов на вертикальную ось:
, (8.3)
где ΔLi - длина i - го интервала; αi - угол кривизны i - го интервала; n - число интервалов, на которое разбивается общая глубина скважины.
При движении жидкости по НКТ она охлаждается и ее плотность немного изменяется. Поэтому необходимо в расчетах принимать среднюю плотность
, (8.4)
где ρс, ρу - плотность жидкости при термодинамических условиях забоя и устья скважины, соответственно. При фонтанировании обводненной нефтью плотность жидкости подсчитывается как средневзвешенная
,
, (8.5)
где n - доля воды в смеси (обводненность); ρн, ρв - плотность нефти и воды в условиях забоя (с) и устья (у) соответственно.
Иногда в результате недостаточной скорости восходящего потока жидкости и оседания воды обводненность n вдоль ствола скважины бывает неодинаковой. Например, между забоем и башмаком НКТ в интервале, где жидкость движется по всему сечению обсадной колонны с малой скоростью, обводненность может быть больше. В таких случаях всю расчетную глубину скважины необходимо разбивать на соответствующие интервалы. Заметим, что погрешности в определении гидростатического давления существенно влияют на все результаты расчета, так как оно преобладает в общем балансе давлений и составляет 95 - 98 % от величины Pс.
Противодавление на устье скважины Pу определяется ее удаленностью от групповой замерной установки, давлением в этой установке или размером штуцера (местного сопротивления), обычно устанавливаемого на выкидной линии фонтанирующей скважины для регулирования ее дебита. При широко распространенных в настоящее время однотрубных, герметизированных системах нефтегазосбора давления на устье Pу бывает большим, достигая иногда нескольких мегапаскалей.
Потери давления на трение Pтр определяются по обычным формулам трубной гидравлики, а именно
. (8.6)
Заметим, что в формуле (8.6) L - не глубина скважины, а длина НКТ вдоль оси скважины. Лишь в вертикальных скважинах эти величины совпадают, поэтому при наклонных скважинах важно учитывать это различие. Скорость жидкости в НКТ Сж определяется обычно через объемный коэффициент жидкости и ее плотность для средних термодинамических условий в НКТ:
, (8.7)
где Qн, Qв - дебит нефти и воды скважины, приведенный к стандартным условиям; ρн, ρв - плотности нефти и воды при стандартных условиях; bн, bв - объемные коэффициенты нефти и воды для средних условий в НКТ; f - площади сечения НКТ (или обсадной колонны для интервала от забоя до башмака НКТ).
При подсчете потерь на трение необходимо учитывать, что диаметр НКТ d существенно влияет на величину Pтр. Это означает, что при уменьшении диаметра НКТ на 10 %, например за счет покрытия внутренней поверхности эпоксидными смолами, стеклом или в результате отложения парафина потери на трение возрастут в 1,61 раза.
Величины коэффициента сопротивления λ определяются через число Рейнольдса по соответствующим графикам или аппроксимирующим формулам. Если такие величины, как Сж, d и ρ, необходимые для определения числа Re оцениваются достаточно точно, то для подсчета вязкости жидкости μ, особенно при движении по НКТ обводненной нефти или эмульсии, нет достаточно точных формул. Вязкость обводненной нефти зависит не только от вязкости компонентов (нефти и воды), но и от дисперсности эмульсии. Тем не менее для оценки этой величины можно рекомендовать следующую приближенную формулу Гатчика и Сабри:
, (8.8)
где μэ - динамическая вязкость эмульсии; μвс - динамическая вязкость внешней дисперсной среды (для эмульсии типа вода в нефти μвс - вязкость нефти, для эмульсии типа нефть в воде μвс - вязкость воды); φ - отношение объема внутренней дисперсной фазы к объему внешней.
При пользовании формулой (8.8) следует иметь в виду, что при обводненности нефти 60 - 70 % происходит инверсия эмульсий, т. е. замещение внешней и внутренней фаз. Поэтому формула (8.8) в представленном написании справедлива для эмульсии с содержанием воды, не превышающим указанных пределов. При большем водосодержании в формулу (8.8) вместо μвс необходимо подставить вязкость внешней среды, которой становится в этом случае вода, и вместо (р подставлять объ
|
|
|
