Основные законы теплового излучения

Лекция 3. Основы теории лучистого теплообмена

Основные определения лучистого теплообмена

Тепловое излучение есть результат превращения внутренней энергии в энергию электромагнитных колебаний. Природа электромагнитных волн одна и та же. Но чисто условно (по мере их исследования) все электромагнитные волны в зависимости от их длины (или частоты) делятся на ряд диапазонов. Волны видимого или светового диапазона (длина волны лежит в пределах от 0,4 до 0,8 мкм) и инфракрасные волны (от 0,8 до 80 мкм) принято называть тепловым излучением.

Следует напомнить, что тела способны не только излучать энергию, но и поглощать ее. Если в рассматриваемой системе находятся тела, имеющие различную температуру, то каждое тело испускает и поглощает различное количество энергии. Вследствие этого одни тела нагреваются, другие охлаждаются.

Но если в системе все тела имеют одинаковую температуру, то в системе устанавливается равновесие: все тела по-прежнему излучают и поглощают энергию, но ее количества равны, т.е. расход энергия равен ее поступлению,

Заметим, что твердые тела и жидкости излучают электромагнитные волны во всем диапазоне частот от 0 до ∞, т.е. имеют сплошной спектр излучения. Но основная доля их излучения приходится на тепловое излучение.

Чистые (неокисленные) металлы и газы характеризуются выборочным (селективным) излучением, т.е. излучают волны только определенной длины.

Поверхностной плотностью интегрального излучения Е называется удельный тепловой поток, т. е. количество тепловой энергии, излучаемой с единицы поверхности в единицу времени на всех длинах волн во всех направлениях.

Излучение, соответствующее узкому интервалу длин волн от λ– d λ до λ+ d λ, называется монохроматическим.

Рассмотрим излучение Е, падающее на поверхность тела (рис. 13.1). Достигнув поверхности, этот пучок разделяется на три части: одна часть — E_R — отражается от поверхности, другая — Е_A — поглощается телом, а третья — E_D — пропускается через него.

Легко составить уравнение баланса энергии:

E = E_R + E_A + E_D

или

E = RE + AE + ДE. (13.1)

В уравнении (13.1) коэффициенты получили следующие названия:

R — коэффициент отражения, ;

A — коэффициент поглощения, ;

D — коэффициент пропускания, .

Из (13.1) следует, что

R + A + D = 1.

 

Рис. 13.1. Распределение энергии излучения, падающего на тело

 

Условно все телa разбиваются на 4 группы. Тела, для которых R =1, называются абсолютно белыми телами, для которых А =1 — абсолютно черными телами, для которых D =1 — абсолютно прозрачными телами. Тела, у которых 0< А <1, называют серыми телами.

Заметим, что в природе все тела– серые.

Поверхность может поглощать инфракрасные лучи, но не поглощать световые лучи. При этом она не выглядит черной. Это относится, например, к снегу, который наше зрение воспринимает как белую поверхность, хотя для снега А =0,98.

Абсолютно черное тело можно моделировать с помощью изотермической замкнутой сферической оболочки, имеющей единственное отверстие (рис. 13.2).

Абсолютно черные тела поглощают (а, следовательно, и излучают) максимальное количество энергии по сравнению с другими телами при одной и той же температуре. Они могут выступать как эталон, с которым целесообразно сравнивать все другие тела.

В заключение дадим понятие лучистого теплообмена.

Лучистым теплообменом называется процесс взаимного излучения, поглощения, отражения и пропускания энергии всеми телами, находящимися в рассматриваемой системе.

 

 

 

Рис. 13.2. Изотермическая замкнутая полость, моделирующая поведение черного тела

 

Основные законы теплового излучения

1. Закон Планка. Данный закон показывает, какая доля энергии, излучаемой абсолютно черным телом, приходится на различные длины волн.

Согласно этому закону спектральная плотность потока энергии излучения абсолютно черного тела при температуре Т и длине волны λ (речь идет о потоке монохроматического излучения) определяется следующим образом:

(13.2)

Здесь l —длина волны; T — температура излучающего тела; С ₁ и С ₂ — постоянные излучения, причем С ₁=3,74∙10^-16 Вт×м², а С ₂=1,44∙10^{-2 м}×К.

В дальнейшем все величины, относящиеся к абсолютно черному телу, будем обозначать с индексом «0».

Распределение энергии по длинам волн показано на рис. 13.3 и 13.4.

2. Закон Вина. Как видно из рис. 13.3, плотность потока при определенной длине волны имеет ярко выраженный максимум. Закон Вина позволяет определить, на какую длину волны приходится этот максимум.

 

 

 

 

Рис. 13.3. Плотность потока монохроматического излучения черного тела

 

Воспользуемся известным методом математического анализа для определения максимума функции.

 

 

Рис. 13.4 Спектральная плотность излучения потока монохроматического излучения как функция длины волны

 

Имеем

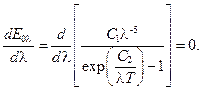
Получим

(13.3)

Здесь λ_max. — это длина волны, на которую приходится максимум излучения абсолютно черного тела, нагретого до температуры Т.

Если подставить выражение (13.3) в (13.2), то получим значение максимального теплового потока.

, Вт/м². (13.4)

Как видно из рис 13.4, с ростом температуры максимума излучения сдвигается в сторону более коротких волн.

Пояснил это на примере. Пропустим через проводник в виде тонкой нити электрический ток так, чтобы проводник нагрелся до 900 К. Если держать руки вблизи проводника, мы почувствуем тепло, которое излучает нить. Но при этом никакого свечения нити наблюдаться не будет. Действительно, при Т =900 К максимум излучения приходится на длину волны 3,2×10^{-6 м, что соответствует области невидимых инфракрасных волн. Повысим силу тока и нагреем нить до 1000 К. В этом случае максимум излучения приходится на красный конец видимого света и мы увидим тускло-красное свечение нити. При Т =1600 К излучением охвачена вся видимая область и нить кажется раскаленной добела.}

Мы видим солнечные лучи, так как поверхность Солнца имеет температуру Т ≈5800 К, при этом λ_max= 5,2∙10^-7м, что приходится на середину видимого спектра. Поэтому Солнце является для нас идеальной «лампочкой».

3. Закон Стефана-Больцмана. Он позволяет определить общее количество теплового потока, излучаемого абсолютно черным телом на всех длинах волн.

Из рисунка видно, что dE_i = E ₀λ _id λ _i.

Площадь под кривой спектральной плотности потока энергии равна полному потоку энергии излучения тела при данной температуре.

(13.5)

Подставим в (13.5) значение Е _0λ из (13.2) и после интегрирования получим следующую зависимость:

(13.6)

Здесь σ₀=5,67∙10^-8 Вт/(м²×К) — постоянная Стефана-Больцмана.

Умножив и разделив правую часть (13.6) на 10⁸, получим более удобную для расчетов формулу

(13.7)

Здесь С ₀=5,67∙Вт/(м²×К) называется коэффициент излучения абсолютно черного тела.

Введем понятие степени черноты

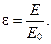(13.8)

Степень черноты — это отношение поверхностной плотности излучения рассматриваемого (серого) тела к поверхностной плотности излучения абсолютно черного тела при той же температуре.

С учетом (13.7) и (13.8) нетрудно заметить, что поверхностная плотность излучения любого тела определяется следующим образом:

 

(13.9)

или

где С =ε С ₀ — называется коэффициентом излучения серого тела.

Степень черноты серого тела может меняться для различных тел от нуля до единицы. Ее значение приводится в теплофизических справочниках. Следует отметить, что ε зависит от состояния поверхности тела. Некоторые значения степени черноты для различных материалов при комнатной температуре приведены в табл. 13.1

В заключение следует отметить, что при комнатных температурах (Т ≈300 К) интегральная плотность излучения на порядок ниже теплового потока при передаче теплоты конвекцией даже для самых небольших значений α и D Т. Поэтому долей теплового излучения в теплообмене при Т ≈300 К можно пренебречь. Но с ростом Т значение Е будет резко возрастать, так как Е ~Т⁴.

4. Закон Кирхгофа. Этот закон устанавливает зависимость между излучательной и поглощательной способностью тела.

Таблица 13.1

Материал	Состояние поверхности	Степень черноты
Алюминий	Полированный	0,04
Шероховатый	0,07
Латунь	Окисленная	0,22
Полированная	0,05
Медь	Окисленная	0,78
Полированная	0,03
Сталь	Окисленная и шероховатая	0,94

 

Рассмотрим теплообмен между двумя параллельными плоскими стенками. Причем одна стенка непрозрачная и серая (D =0, тогда R + А =1), а другая абсолютно черная (рис. 13.5).

Серая стенка излучает энергию Е, которая полностью поглощается абсолютно черной стенкой.

В свою очередь абсолютно черная стенка излучает энергию E ₀. Часть этой энергии AE ₀ поглощается серым телом. Другая часть, равная RE ₀ или (1– A) E ₀, отражается от этой стенки, достигает абсолютно черной стенки иполностью ею поглощается. Будем считать, что рассматриваемые стенки составляют некоторую изолированную систему, т. е. другие тела в теплообмене не участвуют

 

 

 

 

Рис. 13.5. К выводу закона Кирхгофа

 

Составим уравнение энергетического баланса для этих поверхностей. Для серой стенки: поглощается поток энергии AE ₀, a излучается Е, т. е. суммарный излучаемый тепловой поток равен

(13.10)

Для абсолютно черной стенки: излучается тепловой поток энергии Е ₀, а поглощаются E ₀ или (1– A) E ₀, т. е. суммарный излучаемый' поток равен

(13.11)

Будем считать, что тела находятся в термодинамическом равновесии, т. е. Т = Т ₀. Тогда из (13.10) или (13.11) следует, что или

(13.12)

Отсюда

В общем случае для n +1 тела имеем

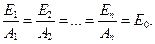(13.13)

Выражение (13.13) является законом Кирхгофа, который утверждает: при термодинамическом равновесии отношение плотности энергии излучения к коэффициенту поглощения есть величина постоянная для всех тел (т. е. не зависит от природы тела) и равна энергии излучения абсолютно черного тела при той же температуре.

Подставим в выражение (13.13) значения Е и Е ₀, полученные с помощью закона Стефана-Больцмана, получим

а после сокращения окончательно

А =ε. (13.14)

Следовательно, коэффициент поглощения тела равен степени его черноты.

Из закона Кирхгофа следует, что большей излучательной способностью обладают тела, которые лучше поглощают тепловую энергию.

5. Закон Ламберта. Этот закон позволяет определить долю поверхностной плотности интегрального излучения энергии, приходящуюся на различные направления по отношению к излучаемой поверхности.

Согласно этому закону (рис. 13.6) максимальная доля энергии излучается в направлении нормали к поверхности. По всем остальным направлениям распределение энергии подчиняется закону косинуса:

(13.15)

(13.16)

Следует отметить, что этотзакон справедлив в полном объеме только для абсолютно черных тел. Для шероховатых серых тел этот закон выполняется только в диапазоне φ=0—60°. Как видно из (13.16), при 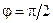Е =0.

				p/2

 

Рис. 13.6. Излучение энергии телом в различных направлениях

 

Поделиться:

Воспользуйтесь поиском по сайту: