Главная | Обратная связь | Поможем написать вашу работу!

Определение ньютоновской и неньютоновских жидкостей. Примеры

Если в движущейся жидкости ее вязкость зависит только от ее природы и температуры и не зависит от градиента скорости, то такие жидкости называют ньютоновскими. К ним относятся однородные жидкости. Плазма является практически ньютоновской жидкостью.

Когда жидкость неоднородна, например, состоит из крупных молекул, образующих сложные пространственные структуры, то при ее течении вязкость зависит от градиента скорости. Такие жидкости называют неньютоновскими.

Вязкость неньютоновских жидкостей увеличивается при уменьшении скорости тока жидкости.

Кровь-неньютоновская жидкость, так как она представляет собой суспензию форменных элементов (эритроциты, лейкоциты и др.) в плазме. Это значит, что из-за различных градиентов скорости, реализующихся в движущейся крови, ее вязкость в различных участках сосудистой системы может изменяться

Жидкости, не подчиняющиеся закону трения (6.1), называются аномальными или неньютоновскими. Неньютоновские жидкости можно разбить на три класса:

1. Стационарно реологические жидкости – касательное напряжение зависит только от градиента скорости:

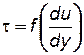. (6.2)

2. Нестационарно реологические жидкости – связь между t и du/dy зависит от времени действия напряжений

. (6.3)

3. Вязкоупругие жидкости – среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений. Для таких сред зависимость между касательными напряжениями и градиентом скорости более сложная; она включает производные по времени как напряжений, так и градиента скорости

Среди неньютоновских жидкостей первого класса, описываемых уравнением (6.2), можно выделить три типа:

1. Вязкопластичные жидкости, для которых уравнение (6.2) имеет вид при t>t₀, (6.4)

при t£t₀.

Рис. 6.1. Зависимость касательного напряжения t от градиента скорости: жидкость: 1 – дилатантная; 2 – ньютоновская; 3 – псевдопластичная; 4 – вязкопластичная

Графическое представление этой зависимости, называемое реологической кривой, приведено на рис. 6.1 (кривая 4 ). В равенство (6.3), кроме коэффициента вязкости m, входит также постоянная t₀,называемая начальным (или предельным) напряжением сдвига. Считается, что при t£t₀ жидкость ведет себя как твердое тело и течение отсутствует. Это объясняется наличием у покоящейся вязкопластичной жидкости пространственной жесткой структуры, сопротивляющейся любому напряжению t, меньшему t₀. Когда t становится больше t₀, структура разрушается.

2. Псевдопластичные жидкости. Эксперименты показали, что для ряда сред связь между напряжением сдвига и градиентом скорости в логарифмических координатах оказывается на некотором участке линейной с угловым коэффициентом от 0 до 1. Поэтому для описания таких сред используется степенная зависимость

, (n < 1), (6.5)

где k и n постоянны для данной жидкости; коэффициент k – мера консистенции жидкости; отличие показателя n от единицы характеризует степень отклонения данной жидкости от ньютоновской. Типичная реологическая кривая (6.4) псевдопластичной жидкости приведена на рис. 6.1 (кривая 3). Модель псевдопластичной жидкости применяется, в частности, для описания движения растворов и расплавов полимеров.

Указанные реологические соотношения можно привести к ньютоновскому виду путем введения понятия кажущейся вязкости m*, как отношения касательного напряжения к градиенту скорости:

Для псевдопластичной жидкости, как следует из (6.4), эта величина 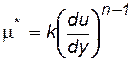и так как n <:1, то m* убывает с возрастанием градиента скорости.

3. Дилатантные жидкости описываются степенным уравнением (6.4), но при n >1. Кривая течения представлена на рис. 6.1 (кривая 1). У этих жидкостей кажущаяся вязкость m*увеличивается с возрастанием градиента скорости. Модель дилатантной жидкости хорошо описывает свойства суспензий с большим содержанием твердой фазы.

В зависимости от вида неньютоновской жидкости по-разному записывается и закон фильтрации. Так закон фильтрации вязкопластичной жидкости (6.3) в пористой среде записывается в виде:

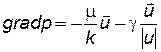u >0; (6.6)

, u =0,

где – – предельный (начальный) градиент.

В соответствии с (6.5) скорость фильтрации u отлична от нуля только в тех областях, где ½gradp½>g (рис. 6.2, кривая 1 ). Модель фильтрации с предельным градиентом следует рассматривать как некоторую идеализацию реальных течений аномальных нефтей в пластовых условиях, для которых реологическая кривая имеет вид кривой 2 на рис. 6.2. Для сравнения на рис. 6.2 показана диаграмма ньютоновской жидкости по закону Дарси (кривая 3 ).

Рис. 6.2. Индикаторные линии: 1 – линейная аппроксимация неньютоновской жидкости; 2 – реальная неньютоновская жидкость; 3 – ньютоновская по закону Дарси

В основе проявления неньютоновских свойств пластовых систем лежат различные физические механизмы, но все неньютоновские эффекты проявляются при малых скоростях фильтрации и в средах с малым размером пор, т.е. с малой проницаемостью. Это определяет особенности неньютоновской фильтрации в неоднородных пластах. Области малой проницаемости оказываются областями наибольшего проявления неньютоновских эффектов.

Так в пластах со слоистой неоднородностью предельные градиенты различны для разных пропластков – чем больше проницаемость, тем меньше предельный градиент g, и наоборот. В связи с этим, пропластки будут последовательно включаться в работу по мере того, как градиент давления будет превышать величины соответствующих предельных градиентов сдвига.

Наряду с рассмотренным законом фильтрации (6.6), описывающим течение вязкопластичной жидкости в пористой среде, рассматривают степенной закон фильтрации:

, (6.7)

где С – экспериментальная константа; n >0.

Степенной закон, соответствующий псевдопластичному флюиду (6.4), хорошо описывает движение растворов полимеров в пористой среде и используется при расчете “полимерного” заводнения пластов с целью повышения их нефтеотдачи.

2. Реологические модели горных пород.

Всякое изменение сил, действующих на горные породы, вызывает их деформацию, а также изменение внутренних усилий – напряжений. Таким образом, динамическое состояние горных пород, как и флюидов, описывается реологическими соотношениями. Обычно реологические зависимости получают в результате анализа экспериментальных данных, натурных исследований или физического моделирования. Если объём пустот не изменяется или изменяется так, что его изменением можно пренебречь, то такую среду можно назвать недеформируемой. Если происходит линейное изменение объёма от напряжения, то такая среда – упругая, иначе ещё её называют кулоновской. К таким средам относятся песчаники, известняки, базальты. В упругих телах при сня-тии нагрузки объём восстанавливается полностью и линия нагрузки совпадает с линией разгрузки. Многие породы деформируются с остаточным изменением объёма, т.е. линия нагрузки не совпадает с линией разгрузки. Такие породы называются пластичными (глины), текучими (несцементируемые пески) или разрушаемыми.

Модели по ориентированности в пространстве. Горные породы необходимо разделять по ориентированности изменения их характеристик в пространстве. С этой позиции выделяют изотропные и анизотропные тела. Изотропия – это независимость изменения физических параметров от направления, анизотропия – различные изменения по отдельным направлениям. Понятие ориентированности, применительно к коллекторам, связано с геометрией расположения частиц, трещин. Частицы горной породы могут располагаться хаотически и упорядочно (иметь геометрическую ориентацию). Упорядочные структуры – ани-зотропны по поверхностным параметрам

Скорость фильтрации

При исследовании фильтрационных течений удобно отвлечься от размеров пор и их формы, допустив, что флюид движется сплошной средой, заполняя весь объём пористой среды, включая пространство, занятое скелетом породы.

Предположим, что через поверхность F пористой среды протекает объёмный расход флюида

Q=`w F_п, (2.1)

где `w – действительная средняя скорость жидкости; F_п – площадь пор.

Площадь пор связана с полной поверхностью через просветность (соотношение 1.2), а для сред неупорядочной структуры справедливо допущение о равенстве просветности и пористости. Следовательно,

Q=`w m F. (2.2)

Величина

u= `w m (2.3)

называется скоростью фильтрации и определяет переток флюида, осреднённый по площади. Так как m<1, то скорость фильтрации всегда меньше средней.

Физический смысл скорости фильтрации заключается в том, что при этом рассматривается некоторый фиктивный поток, в котором:

· расход через любое сечение равен реальному расходу,

· поле давлений идентично реальному потоку,

· сила гидравлического сопротивления равна силе сопротивления реального потока.

Предполагается, что скорость фильтрации непрерывно распределена по объёму и связана со средней действительной скоростью течения равенством (2.3).

4. Потенциа́льное тече́ние — безвихревое движение жидкости или газа, при котором деформация и перемещение малого объёма жидкости происходит без вращения (вихря). При потенциальном течении скорость жидкости может быть представлена следующим образом:

{\displaystyle {\vec {v}}=\nabla \phi (x,y,z)}

где {\displaystyle \phi (x,y,z)} — некоторая скалярная функция, называемая потенциалом скорости течения. Движение реальных жидкостей будет потенциальным в тех областях, где действие сил вязкости ничтожно мало по сравнению с действием сил давления и в которых нет завихрений, образовавшихся за счёт срыва со стенок пограничного слоя или за счёт неравномерного нагревания. Необходимым и достаточным условием потенциальности течения являются равенства:

ПЛОСКОРАДИАЛЬНЫЙ ПОТОМ

Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.

а) Горизонтальный пласт постоянной толщины (h) и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рис. 3.2), т.е. вскрыт на всю толщину и забой полностью открыт. Для эксплуатационной скважины поток - радиально-сходящий, а для нагнетательной - радиально-расходящий. Плоско-радиальным потоком будет занята вся зона от стенки скважины до контура питания.

б) Гидродинамически- несовершенная скважина - вблизи скважины линии тока искривляются и поток можно считать плоско-радиальным только при некотором удалении от скважины.

в) Круговая батарея эксплуатационных скважин - поток плоско-радиален на некотором удалении, т.к. жидкость движется как бы к укрупнённой скважине радиуса, равного радиусу окружности батареи.

6. Радиально-сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.

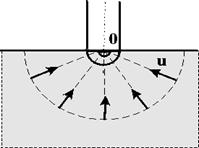Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.

{\displaystyle {\frac {\partial v_{x}}{\partial y}}={\frac {\partial v_{y}}{\partial x}},\quad {\frac {\partial v_{x}}{\partial z}}={\frac {\partial v_{z}}{\partial x}},\quad {\frac {\partial v_{y}}{\partial z}}={\frac {\partial v_{z}}{\partial y}}}

7. Вязкоупругие жидкости – среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений. Для таких сред зависимость между касательными напряжениями и градиентом скорости более сложная; она включает производные по времени как напряжений, так и градиента скорости

Вязкопластичные жидкости

для которых уравнение (6.2) имеет вид при t>t₀, (6.4)

при t£t₀.

Интерференция скважин

Взаимодействие работающих нефтяных, газовых или водяных скважин, пробурённых с поверхности на один продуктивный пласт или на разные, но гидродинамически связанные друг с другом пласты. И. с. обусловлена тем, что нефть, газ, вода подвижны, а поры продуктивных пластов, в которых они содержатся, связаны в единую систему поровых каналов и трещин. При этом скважины одинакового назначения «мешают» друг другу, перехватывая притекающую к ним жидкость (или газ). В результате дебит каждой из нескольких работающих скважин всегда меньше дебита единичной скважины при прочих равных условиях. Этот факт обусловливает принципиальную особенность разработки месторождений жидких (газообразных) полезных ископаемых: все эксплуатационные нефтяные (газовые или водяные) скважины рассматриваются только в совокупности — в их взаимодействии в общем технологическом процессе разработки.

В случае интерференции скважин несовершенных по степени вскрытия в условиях течения по закону Дарси вначале определяется дебит совершенных скважин радиусами r_с по формулам теории интерференции для притока к стокам и источникам на плоскости, а затем фильтрационное сопротивление каждой скважины увеличивается на величину коэффициентов несовершенства С_i (i =1,...,4). Если определены коэффициенты фильтрационных сопротивлений А_н и В_н, указанным выше аналитическим оценочным методом или прямым испытанием скважины путем пробных откачек при установившемся режиме, можно использовать метод эквивалентных фильтрационных сопротивлений для исследования интерференции несовершенных скважин, в том числе при двухчленном законе фильтрации. Для этого двухчленный закон надо представить в виде

, 4.56

где 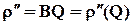можно рассматривать как нелинейное сопротивление, добавляемое к внутреннему сопротивлению r, определяемому конечным расстоянием между скважинами в батарее.

Например, в схеме фильтрационных сопротивлений для условий линейного закона фильтрации, внутренние сопротивления r следует заменить суммой 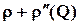, где 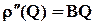для каждой скважины. Дальнейший расчет ведется, как и ранее, при помощи законов Ома и Кирхгофа, но система уравнений получается уже не линейной, а содержащей квадратные уравнения, что приводит к усложнению вычислений.

10. Объемный газовый фактор – отношение объемного газового дебита, приведенного к давлению в 1 ат, к объемному дебиту жидкого компонента, приведенному к тем же условиям.

11. Объемный коэффициент нефти b (р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина b(р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях.

Согласно данному определению .

Заменяя в формуле (5.18) отношение функцией Y(s) получим:

12.Сущность моделирования процессов фильтрации флюидов в пластах заключается в определении количественной связи между дебитами и давлениями на забоях скважин и определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, вязкости флюидов, числа и расположения скважин.

При решении фильтрационных задач можно выделить прямые и обратные задачи.

13.Прямые задачи – задачи, в которых свойства пласта и жидкостей, а также «начальные и граничные» условия считаются известными.

Прямые активные задачи – задачи определения полей давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте – объекте разработки с системой скважин. Знание этих полей позволяет рассчитывать технологические показатели работы нефтяных и нагнетательных скважин.

Прямые пассивные задачи – определение конфигурации подвижной границы нефтяной зоны и скорости ее продвижения с целью установления сроков прорыва вытесняющего флюида в скважины и вычисления текущего коэффициента нефтеотдачи.

В одножидкостной модели определение подвижной границы сводится к прослеживанию линии отмеченных частиц в однородной жидкости. Для решения задачи оценки скорости продвижения контура нефтеносности используются поле пластовых давлений, поле проницаемости, текущее положение контура водо-нефтяного контакта. Скорость оценивается картой линий тока. Сгущение изолиний на картах равных значений пластового давления (карты изобар) может быть вызвано двумя причинами: ухудшением проницаемости и увеличением скорости отбора жидкости скважинами. Эти два фактора можно разделить, если учесть продуктивность скважины: высокая продуктивность связана с хорошей проницаемостью пласта. По наборам карт изобар могут быть определены параметры гидропроводности и проницаемости.

Воспользуйтесь поиском по сайту: