Список использованой литературы

ВВЕДЕНИЕ

 

Математическая модель — математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект или процесс, построенный на этапе содержательного моделирования. Математическая модель позволяет предсказать поведение реального объекта.

Программный комплекс автоматизированного динамического анализа многокомпонентных механических систем EULER (ЭЙЛЕР) разработан специалистами ООО «АвтоМеханика» с участием преподавателей и аспирантов Московского государственного университета им. М.В. Ломоносова.

Программный комплекс предназначен для анализа работы механических систем, включающих в себя сложную кинематику, большие движения, жесткие и деформируемые элементы конструкции, гидравлические, пневматические и электрические системы, системы управления и другие компоненты.

В программном комплексе EULER реализована оригинальная технология автоматизированного динамического анализа многокомпонентных механических систем. Суть технологии состоит в следующем. Описание динамической модели механической системы производится в обычных инженерных терминах, таких как тело, шарнир – кинематическая связь, упругий или демпфирующий элемент силового взаимодействия и т.д. Такое описание модели может быть выполнено специалистом – инженером. На основании инженерно-технического описания динамической модели автоматически формируется математическая модель движения исследуемой механической системы в соответствии с концепцией динамического взаимодействия множества твердых и упругих тел. Уравнения этой математической модели точно соответствуют законам классической механики с учетом больших перемещений частей механической системы и учетом нелинейных характеристик взаимодействий. По сравнению с традиционным подходом к исследованию динамики сложных механических систем, при котором производится «ручное» формирование уравнений и их программирование, технология автоматизированного динамического анализа обеспечивает многократное уменьшение времени создания динамических моделей сложных объектов и высокую гибкость по их перенастройке.

Программный комплекс EULER может применяться при проектировании, отработке, испытаниях и доводке различных изделий, в научных и прикладных исследованиях, а также в процессе обучения. Программным комплексом могут пользоваться инженеры, научные работники и студенты различных отраслей науки и промышленности. Использование программного комплекса позволяет уже на ранних стадиях проектирования получить достоверную информацию о поведении и силовых нагрузках в создаваемых изделиях. С помощью математических моделей можно определять характеристики работы новых систем, оптимизировать их параметры и проводить сравнительный анализ различных вариантов конструкции. Программный комплекс EULER также позволяет оперативно проводить исследования нештатных ситуаций, возникающих в процессе эксплуатации существующих систем. В результате, сокращаются сроки разработки, существенно уменьшается объем доводочных испытаний, повышается качество изделий и снижаются затраты на их создание.

LS-PrePost является как препроцессором, так и постпроцессором, другими словами в нем можно как создать модель, так и посмотреть результаты расчета.

Программа предназначена для решения трёхмерных динамических нелинейных задач механики деформируемого твёрдого тела, механики жидкости и газа, теплопереноса, а также связанных задач. LS-DYNA нашла широкое применение в таких отраслях науки и техники, как автомобилестроение (симуляция краш-тестов), военно-промышленный комплекс (симуляция взрывов боеприпасов и их воздействие на окружающие предметы), авиа- и ракетостроение (проектирование реактивных двигателей и сопел) и так далее.

В LS-DYNA реализованы явный и неявный метод конечных элементов с возможностью построения лагранжевой, эйлеровой и гибридной сетки, многокомпонентная гидродинамика, бессеточный метод сглаженных частиц, бессеточный метод, основанный на методе Галеркина. Программа имеет встроенные процедуры автоматической перестройки и сглаживания конечно-элементной сетки при вырождении элементов, высокоэффективные алгоритмы решения контактных задач, широкий набор моделей материалов, возможности пользовательского программирования.

 

ЗАДАНИЕ №1

 

С помощью разработанной математической модели в программном комплексе Эйлер решить задачу. Груз массой М веса Р падает без начальной скорости с высоты Н на плиту А лежащую на спиральной пружине В. От действия упавшего груза М пружина сжимается на величину h. Не учитывая сопротивлений вычислить время Т сжатия пружины на величину һ и импульс S упругой силы. Упругой силы пружины за время Т. Исходные данные: Р = 50 Н; Н = 0,3 м; масса плиты А = 1 кг; жесткость пружины: 1500 Н/м.

Провести расчет для трёх разных коэффициентов демпфирования пружины.

 

Рисунок 1 – Схема модели.

 

ПОСТРОЕНИЕ МОДЕЛИ

 

На рисунке 1 представлено изображение объектов расчета. Груз (5 кг) расположен над плитой (1 кг) на расстоянии Н = 0,3 м. Между плитой и неподвижной опорой (инерциальным телом) расположена пружина (жёсткость пружины = 1500 Н/м, длина пружины Н = 0,3 м). Объекты созданы в программе Euler путем построения точек, созданием геометрии объектов и присвоением им массы. Далее, для получения необходимых взаимосвязей необходимо связать объекты, точки и узлы каждого тела по звеньям.

 

Рисунок 2 – Описание модели.

 

 

 

ПРОВЕДЕНИЕ РАСЧЕТОВ

 

В модели время расчета равно 1-ой секунде. На рисунке 2 модель изображена в начале расчета.

Рисунок 3 – Модель в начале расчета.

 

На груз и плиту действует сила притяжения. И, пока груз падает, плита немного опускается под действием собственного веса. Плита свободно колеблется, пока груз не коснулся поверхности плиты (Рисунок 4).

Рисунок 4 – Модель в середине расчета.

 

В ходе упругого удара груза об плиту, груз и плита давят на пружину, в следствии чего пружина сжимается сильнее. Это происходит за интервал времени Т. В точке изменения направления движения плиты и груза, пружина сжалась на максимальное значение h (Рисунок 5). 

Рисунок 5 – Модель в конце расчета.

 

Так же, в этом положении, в пружине возникает максимальный импульс силы S, который находится, как:

 , где

f – Сила сжатия пружины

 - Момент касания груза с плитой

 - Момент достижения максимального значения силы сжатия пружины

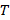 - интервал времени за который сжалась пружина

 

Далее представлены расчеты при различных коэффициентах демпфирования:

1. При коэффициенте демпфирования равном 50 Нс/м

 

График изменения расстояния h по времени t (Рисунок 6), по которому определяем интервал сжатия пружины T. В данном случае T = 0,11 с.

-

Рисунок 6 - График изменения расстояния h.

 

 

Рисунок 7 - График изменения силы.

 

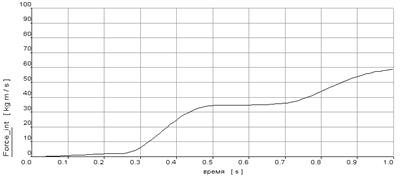
Рисунок 8 - График изменения импульса.

2. При коэффициенте демпфирования равном 100 Нc/м

 

Рисунок 9 - График изменения расстояния h.

 

 

Рисунок 10 - График изменения силы.

Рисунок 11 - График изменения импульса.

3. При коэффициенте демпфирования равном 150 Нc/м

 

Рисунок 12 - График изменения расстояния h.

 

 

Рисунок 13 - График изменения силы.

Рисунок 14 - График изменения импульса.

 

Также, необходимо найти наибольшее расстояние h и наибольшее значение импульса упругой силы S, определение которых происходит с помощью поиска максимального значения показанных выше графиков функций. Значения приведены в таблице 1.

 

Таблица 1

Коэффициент Демпфирования пружины, Нc/м	Максимальное значение h, м	S, Н ∙ с	T, c
50	0,15926	56
100	0,15072	48	0,11
150	0,14425	45

 

 

ЗАДАНИЕ №2

 

Разработать с помощью программного комплекса LS-Dyna модель грудной клетки CWVP (Chest Wall Velocity Predictor) Рисунок 15. Приложить к грудной клетке избыточное давление, имеющее зависимость неравнобедренного треугольника с пиком амплитуды при 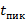 = 0,1t. Значение t принять равным 10, 20, 30 мс, при амплитуде давления равным 0.3, 0.6, 0.9 атм. Построить график скорости стенки грудной клетки для всех вариантов расчета.

 

 

 

A: Эффективная площадь

M: Эффективная масса

V: Начальный газообразный объем легких

X: Смещение

C: Коэффициент демпфирования

K: Константа эластичности

: Атмосферное давление

P(t): Избыточное давление

γ: Политропный компонент газа в легких

 

Модель представляет собой дифференциальное уравнение второго порядка (нелинейное) и необходимо использовать следующие значения для констант модели (для мужчины весом 70 кг):

 

 

A = 0,082  

M = 2,03 кг

C = 696 Нс / м

K = 989 Н / м

V = 1,82 *

 = 1,0 *  Па

Y = 1.2

 

Для оценки травмы необходимо рассчитать профиль скорости (dx / dt). Эта скорость называется предиктором скорости стенки грудной клетки (CWVP).

 

ПОСТРОЕНИЕ МОДЕЛИ

 

Модель строилась в программе LS PrePost. Для ее создания использовались данные стандарта модели CWVP. В этой модели, стенка грудной клетки представлена отдельным телом и может перемещаться относительно другого тела, представляющее собой оставшуюся часть человеческого тела. Модель стенки грудной клетки представляет собой создание двух параллелепипедов на некотором расстоянии друг от друга, между которыми присутствует пружина и демпфер рисунок 16.

 

Рисунок 16 – Модель стенки грудной клетки.

 

После геометрического создания объектов, ограничим перемещение тела, относительно которого двигается модель по всем направлениям, а передвижение стенки грудной клетки только по одной оси Z.

Далее, создадим материал модели грудной клетки и материал модели легкого. Для этой модели они должны быть абсолютно жесткими.

Создадим материал для пружины, так же указываем ее жесткость, которая задана в условии.

Создадим тип элемента для грудной клетки и для пружины.

Присвоим тип и материал для легкого, грудной клетки и пружины.

Создадим графики избыточного давления на грудную клетку (Рисунки 17 - 25) и присвоим нагружение модели грудной клетки.

Рисунок 17 - График избыточного давления для 0,3 атм. при 10 мс.

 

Рисунок 18 - График избыточного давления для 0,3 атм. при 20 мс.

 

Рисунок 19 - График избыточного давления для 0,3 атм. при 30 мс.

Рисунок 20 - График избыточного давления для 0,6 атм. при 10 мс.

 

Рисунок 21 - График избыточного давления для 0,6 атм. при 20 мс.

 

Рисунок 22 - График избыточного давления для 0,6 атм. при 30 мс.

Рисунок 23 - График избыточного давления для 0,9 атм. при 10 мс.

 

Рисунок 24 - График избыточного давления для 0,9 атм. при 20 мс.

 

Рисунок 25 - График избыточного давления для 0,9 атм. при 30 мс.

Для корректного расчета, необходимо использовать рассеивание энергии, включающее энергетический баланс.

Для того, чтобы расчет не был бесконечным, зададим время расчета t из условия. Так же укажем параметры расчета:

Шаг интегрирования;

Количество кадров визуализации;

Частоту написания базы данных.

Для того, чтобы поставить демпфер, необходимо выбрать точки, между которыми он будет работать. Для удобства, используем уже имеющиеся и указываем те же, что у пружины. Зададим материал демпферу и укажем коэффициент демпфирования из условия. Используем PART для присваивания демпферу его характеристик.

Финальным этапом является компиляция в LS DYNA manager.

 

 

ПРОВЕДЕНИЕ РАСЧЕТОВ

 

Так как, отображение перемещения модели при нагрузках 0,3, 0,6 и 0,9 атм. отличаются только тем, что при увеличении нагрузки тело перемещается чуть больше, на рисунках 25-27 модель изображена в начале, середине и конце расчета, для средней нагрузки 0,6 атм., соответственно.

 

Рисунок 25 – Модель в начале расчета.

 

Рисунок 26 – Модель в середине расчета.

Рисунок 27 – Модель в конце расчета.

 

Далее, необходимо найти графики и выделить максимальные значения графиков скорости модели грудной клетки при трёх различных значениях давления и времени приложения нагрузки.

Для отыскания скорости моделей грудной клетки, необходимо использовать вкладку History, в которой можно выделить, как одну точку, так и все тело, после чего выбрать скорость по оси Z, так как модель грудной клетки перемещается именно по ней, и, собственно, построить графики.

Графики изменения скорости моделей грудной клетки представлены на рисунках 28 - 36.

 

 

Рисунок 28 - График скорости стенки грудной клетки для 0,3 атм. при 10 мс.

 

Рисунок 29 - График скорости стенки грудной клетки для 0,3 атм. при 20 мс.

 

Рисунок 30 - График скорости стенки грудной клетки для 0,3 атм. при 30 мс.

Рисунок 31 - График скорости стенки грудной клетки для 0,6 атм. при 10 мс.

 

Рисунок 32 - График скорости стенки грудной клетки для 0,6 атм. при 20 мс.

 

Рисунок 33 - График скорости стенки грудной клетки для 0,6 атм. при 30 мс.

Рисунок 34 - График скорости стенки грудной клетки для 0,9 атм. при 10 мс.

 

Рисунок 35 - График скорости стенки грудной клетки для 0,9 атм. при 20 мс.

 

Рисунок 36 - График скорости стенки грудной клетки для 0,9 атм. при 30 мс.

Зависимость максимальной скорости стенки грудной клетки от приложенного давления представлена в Таблице 2.

 

Таблица 2

Избыточное давление, атм.	Время импульса, с	Максимальная скорость стенки грудной клетки, м/с
0,3	0,01	2
0,6	0,01	2,4
0,9	0,01	2,7
0,3	0,02	4
0,6	0,02	5
0,9	0,02	5,5
0,3	0,03	6
0,6	0,03	7,5
0,9	0,03	8,2

 

 

ЗАКЛЮЧЕНИЕ

 

1. В ходе выполнения первого задания, была рассчитана математическая модель груза, падающего на плиту, прижимающую пружину.

Определяемые параметры:

1.1. Время сжатия пружины до максимального сжатия пружины под действием упавшего груза;

1.2. Деформация пружина относительно первоначального положения;

1.3. Импульс упругой силы пружины.

Результаты расчётов при различных коэффициентах демпфирования представлены в таблице 1. Стоит отметить, что изменением времени сжатия пружины при изменении коэффициента демпфирования можно пренебречь, при текущих размерах модели.

Максимальное расстояние, на которое сжалась пружина, при увеличении коэффициента демпфирования, уменьшалось, а, импульс упругой силы, наоборот, увеличивался.

2. Во второй расчетно-графической работы была рассчитана модель грудной клетки к которой прикладывалось различное избыточное давление для расчёта скорости грудной клетки. Далее, исходя из таблицы 3, следует, что:

При избыточном давлении 0,3 атм. и времени импульса 10 мс, а также, при избыточном давлении 0,6 и 0,9 атм. и времени импульса равным 10 мс, скорость стенки грудной клетки не превышает 3,6 мс, что является допустимым значением для безвредной скорости.

При времени импульса 20 мс. и избыточном давлении равном 0,3; 0,6 и 0,9 атм., а также, при времени импульса 30 мс. и избыточном давлении равном 0,3 и 0,6 атм., скорость стенки грудной клетки входит в диапазон от легкой до слабой травмы.

При времени импульса 20 мс. и избыточном давлении равном 0,6 и 0,9 атм., а также, при времени импульса 30 мс. и избыточном давлении равном 0,3; 0,6 и 0,9 атм., скорость стенки грудной клетки входит в диапазон от слабой до средней травмы.

При времени импульса 30 мс. и избыточном давлении равном 0,6 и 0,9 атм., скорость стенки грудной клетки входит в диапазон от средней до обширной травмы.

 

Таблица 3

Уровень травмы	V, м/с
Безвредная (не травма)	0,0 – 3,6
От легкой до слабой	3,6 – 7,5
От слабой до средней	4,3 – 9,8
От средней до обширной	7,5 – 16,9
> 50% смертельная	> 12,8

 

 

СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ

 

1. EULER.RU: Главная страница [Электронный ресурс] / Режим доступа: http://www.euler.ru, свободный. – Загл. с экрана.

2. Математическая модель [Электронный ресурс]: Материал из Википедии — свободной энциклопедии: Версия 100530739, сохранённая в 12:19 UTC 20 июня 2019 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2019. — Режим доступа: https://ru.wikipedia.org/?oldid=100530739

3. Паниченко, И.В. Расчетно-графическая работа на тему: «Разработка математической модели сброса энергопоглащающего кресла в составе с антропоморфным измерительным манекеном (АИМ)» / И.В. Паниченко. – М.: МПУ, 2018. – 33 с.

4. LS-DYNA [Электронный ресурс]: Материал из Википедии — свободной энциклопедии: Версия 100067922, сохранённая в 16:27 UTC 27 мая 2019 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2019. — Режим доступа: https://ru.wikipedia.org/?oldid=100067922

 

 

Поделиться:

Воспользуйтесь поиском по сайту: