 |
Многомерные стационарные задачи теплопроводности
|
|
|
|
Размерные величины и единицы измерения
Размерной величиной называется любая измеряемая величина. Прежде, чем проводить численные расчеты, нужно выразить каждую размерную величину в определенных воспроизводимых единицах измерения. Единицы измерения – это произвольно выбранные меры, которые позволяют определить количественно каждую размерную величину.
В настоящее время в мире используется несколько различных систем единиц измерения. В промышленности, науке и технике быстро распространяется и становится общепринятой система СИ (международная система единиц). Система СИ была принята Международной организацией по стандартизации и рекомендована многочисленным национальным организациям по стандартизации.
В таблице указаны основные единицы измерения системы СИ и других общеупотребляемых систем.
Теория размерностей
Теорию размерностей можно применить в большинстве задач, используя следующую методику. 
Формулы размерности физической величины вытекает из определения или из физических законов. Формула размерности длины стержня записывается по определению. Как [L]. Средняя скорость частицы жидкости равна расстоянию, деленному на время, которое было затрачено на преодолении этого расстояния. Следовательно, формула размерности [L/Q] или [LQ-1] (т.е. длина, деленная на время). Квадратные скобки означают, что величина имеет формулу размерности, стоящую в скобках. В таблице ниже представлены обозначения и формулы размерности физических величин, часто встречающихся в задачах теплопередачи. 
Уравнение теплопроводности
Уравнение теплопроводности является математическим выражением закона сохранения энергии в твердом веществе. Оно выводится из рассмотрения баланса энергии для элементарного объема материала. Закон Фурье: 
, где q – удельный тепловой поток, (Дж/(с*К);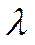 
- коэффициент теплопроводности, (Вт/м*К)); dT/dx – градиент температуры (показывает направление возрастания температуры. Знак минус показывает, что тепловой поток идет в обратную сторону.
|
|
|
(входит)
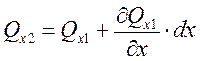(выходит)
; 
; 
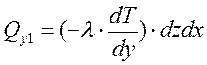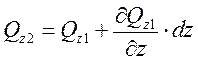
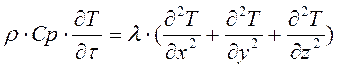- уравнение теплопроводности
- энергия, получаемая элементом dxdydz в единицу времени; 
- коэффициент температуропроводности
Одномерная стационарная задача теплопроводности при отсутствии внутреннего тепловыделения
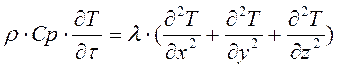- уравнение теплопроводности
таким образом получили: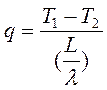 
- тепловое сопротивление
Влияние переменности коэффициента теплопроводности
Коэффициент теплопроводности большинства материалов не является постоянной величиной, а зависит от температуры.
Предположим, что величина коэф. теплопроводности переменна:
Для стационарного одномерного распределения температуры в прямоугольном твердом теле при отсутствии внутреннего тепловыделения: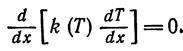 
Зависимость коэф. теплопроводности от температуры: 
; 
.
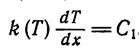
Зададим граничные условия: 
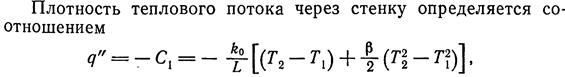
Одномерная стационарная задача теплопроводности при наличии внутреннего тепловыделения
условия, находим распределение температуры в твердом теле: 
Перенос тепла в ребрах
Интенсивность рассеяния тепла с поверхности можно повысить, просто увеличивая эту поверхность. Это достигается при помощи рёбер.
Тепло распространяется вдоль твердого материала ребра посредством теплопроводности и отводится от его поверхности окружающей жидкостью посредством конвекции.
; 
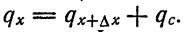, Р- периметр ребра
; 
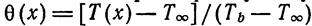Тb – температура основания ребра
Следовательно 
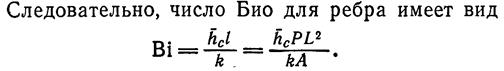
Безразмерное уравнение переноса тепла в ребре:
Многомерные стационарные задачи теплопроводности
Для решения 3-хмерной задачи параллелепипеда используется метод произведения решений 3-хмерных задач для бесконечных пластин:
|
|
|
Решение 2-хмерных стационарных задач методом релаксации
Уравнение Лапласа: 
Алгоритм решения задачи:
Будем считать, что 
+ 
=0
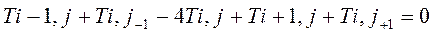
-(это условие всегда должно выполняться!)
|
|
|
