Методы статистического изучения взаимосвязи социально-экономических явлений.

БИЛЕТ № 55.

1. Издержки и прибыль фирмы.

2. Методы статистического изучения взаимосвязи социально-экономических явлений.

3. Перестрахование как операция по достижению финансовой устойчивости страховщика.

 

Издержки и прибыль фирмы

Издержки – это денеж.выражение затрат производственных факторов, необходимых для осущ-ния предприятием своей производственной и реализационной деят-ти.

Альтернативные издержки – ценность других благ, которые можно было бы получить при наиболее выгодном из всех доступных альтернативных способов использ-ния данного ресурса. Альт. Изд-ки можно опр-ть как величину дохода, которая необходима, чтобы отвлечь конкретный ресурс от произв-ва данного товара и использовать его для произв-ва др. товара.

В краткоср.периоде часть ресурсов не изменяется, а часть ресурсов является переменной. В эк. анализе применяются условные деления на постоянные и переменные издержки произв-ва.

В долгоср. периоде: поскольку в длительном периоде времени все ресурсы являются переменными, поэтому и все издержки произв-ва явл-ся переменными, т.е. отсутствует деление на постоянные и переменные издержки.

Издержки фирмы в краткосрочном периоде.

Постоянные издержки (FC) – это часть общих издержек, величина кот-х не зависит от объема выпуска и их значение постоянно. В свою очередь пост. изд-ки делятся на: стартовые – та часть пост.изд-ек, кот-я возникает при возобновлении произв-ва, остаточные – та часть пост.изд-ек, кот-ю продолжает нести фирма, даже если произв-во продукции временно прекращено.

Переменные издержки (VC) – часть общих издержек, величина кот-х зависит от объема выпуска. Их динамика в краткоср. периоде опр-ся действием закона убывающей предельной производит-ти. Поэтому различают: пропорциональные, прогрессивные и регрессивные изд-ки.

Пропорц.перемен.изд-ки – это ситуация, когда относит-ное изменение перем-х изд-ек равно относит-но изменению объема выпуска продукции.

Прогр.перем.изд-ки – ситуация, когда относит-ный рост перем-х изд-ек больше, чем относит-ное увел-ние объемов произв-ва.

Регресс.перем.изд-ки – ситуация, когда относит-ное изменение перем-х изд-ек меньше, чем относит-ный рост объема выпуска продукции.

Совокупные издержки (TC) – изд-ки, кот-е предст-ют собой денеж.выражениеи расходов, связанных с изготовлением продукции. (ТС = FC + VC)

Предельные издержки (MC) – приращение валовых изд-ек произв-ва в рез-те увел-ния объема выпуска на одну дополнит. ед-цу. (MC = ∆ TC / ∆ Q )

Средние постоянные издержки (AFC) – это величина постоянных изд-ек, приходящихся в среднем на ед-цу продукции. (AFC = FC / Q)

 

Средние переменные издержки (AVC) – это величина переменных изд-ек, приходящихся в среднем на ед-цу продукции. (AVC = VC / Q)

Средние общие издержки (ATC) – величина валовых изд-ек, приходящихся в среднем на ед-цу продукции.

(АТС = ТС / Q или АТС = AFC + AVC)

Закон убывающей предельной производительности: При прочих равных условиях, при неизменности большинства факторов производства последующее применение дополнительных единиц переменного ресурса сопротивляется снижением его отдачи.

В долгоср.периоде все ресурсы фирмы являются переменными. Фирма может нанять новое оборуд-е, арендовать новые цеха, изменить состав управленч-го персонала, использовать новую технологию произв-ва.

Отсутствие в долгоср.периоде постоянных ресурсов ведет к тому, что исчезает разница между постоянными и переменными издержками. Анализ долгоср.деят-ти фирмы проводится ч/з рассмотрение динамики долгоср. средних издержек (LAТC). А основной целью фирмы в области изд-ек можно считать орг-цию произв-ва "нужного масштаба", обеспеч-щего заданный объем продукции с минимал. средними издержками.

Отдача от масштаба произв-ва - взаимосвязь между изменением масштаба произв-ва и соответствующим изменением в объеме выпуска продукции.

Валовой (общий) доход (TR) – предст-ет собой денеж. выражение суммарного дохода, получаемого фирмой от реализации опред-го колич-ва продукции по опред. цене. (TR = PQ)

Средний доход (AR) – доход, приходящийся в среднем на ед-цу реал-ции продукции. (AR = TR / Q)

Предельный доход (MR) – это приращение общего дохода в рез-те роста объема выпуска на дополнит-ную ед-цу продукции. (MR = ∆ TR / ∆ Q)

Прибыль – превышение дохода фирмы над издержками произв-ва и реализации продукции.

Общая прибыль (ТП) – разность между валовым доходом и совокупными издержками произв-ва. (ТП=TR-TC)

Средняя прибыль (АП) – предст-ет собой часть валовой прибыли, приходящейся в среднем на ед-цу продукции. (АП=ТП/Q= AR-ATC

)

Предельная прибыль (МП) – приращение общей прибыли в рез-те изменения объема реализации на дополнительную единицу. (МП=MR-MC)

Бухгалтерская прибыль – прибыль, равная разнице между суммарной выручкой фирмы и бухг. (внешними) издержками, связанными с произв-вом и реализацией продукции. (П бух = TR – С бух)

Экономическая прибыль – разница между суммарной выручкой и альтернативными издержками фирмы.

П эк = TR – С эк = TR – (C бух + С неявн) = П бух – С неявн

Методы статистического изучения взаимосвязи социально-экономических явлений.

Методы статистического изучения взаимосвязи социально-экономических явлений.

Понятие причинности применяется всегда, когда осуществление одного события оказывается достаточным основанием для ожидания того, что произойдет другое событие. В этом случае первое событие выступает причиной, а второе - следствием.

В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых массовых явлений и процессов.

Между явлениями и их признаками различают прежде всего два вида связей:

функциональные и стохастические, каждая из которых имеет свои особенности. Частным случаем стохастических связей являются корреляционные.

Функциональные - Каждому значению величины факторного признака соответствует только одно или несколько точно определённых значений результативного признака.

Она обычно выражается формулами, что в большей степени присуще точным наукам.

Функциональная зависимость с одинаковой силой проявляется у всех единиц совокупности. Она является полной и точной, так как обычно известны перечень всех факторов и механизм их воздействия на результативный признак в виде

уравнения

Статистическое изучение связи между причиной и следствием состоит из нескольких этапов.

На первом этапе изучается качественный анализ рассматриваемого явления, связанный с анализом природы явления. На втором этапе строится модель связи. Этот этап базируется на методах статистики: группировках, средних величинах, таблицах и т.д. На третьем, последнем этапе осуществляется интерпретация результатов. Этот этап так же, как и первый, связан анализом природы изучаемого явления.

Корреляция - это статистическая зависимость между величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению другой величины.

В статистике принято различать следующие варианты зависимостей:

1. Парная корреляция - связь между двумя признаками (результативным и факторным или между двумя факторными);

2. Частная корреляция - зависимость между результативным и одним факторным признаком при фиксации значений других факторных признаков;

3. Множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками: при парной корреляции - между двумя признаками; при множественной корреляции - между несколькими.

Задачи и предпосылки применения корреляционно-регрессионного анализа

Корреляционный анализ изучает взаимозависимости показателей и позволяет решить следующие задачи:

1. Задача оценки тесноты связи между показателями с помощью парных, частных и множественных коэффициентов корреляции;

2. Задача оценки уравнения регрессии.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (У) от факторных (Х1, Х2,..., Хк).

Уравнение регрессии, или статистическая модель связи массовых процессов и явлений, выражаемая функцией

Ух = Ф (Х1, Х2,..., Хк), является достаточно адекватным реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построения:

1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями;

2. Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей;

3. Все факторные признаки должны иметь количественное (цифровое) выражение;

4. Наличие достаточно большого объема исследуемой выборочной совокупности;

5. Причинно-следственные связи между явлениями и процессами следует описывать линейной или приводимой к линейной формами зависимости;

6. Отсутствие количественных ограничений на параметры модели связи;

7. Постоянство территориальной и временной структуры изучаемой совокупности.

Основной проблемой построения уравнения регрессии является его размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным, то есть наилучшим.

Парная регрессия характеризует связь между двумя признаками: результирующим и факторным. Аналитическая форма записи этой связи имеет вид: прямая - гипербола - параболы -

Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Откуда система нормальных уравнений для нахождения параметров линейной регрессии имеет следующий вид:

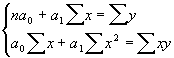
где n - число наблюдений.

Расчет параметров уравнения линейной регрессии: а₀ ,

a₁ = y – а₀x.

В уравнениях регрессии параметр показывает усредненное влияние на результативный признак неучтенных факторов; - коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения

Нахождение уравнения регрессии по сгруппированным данным. Если совокупность сгруппирована по признаку x, для каждой группы найдены средние значения другого признака у, то эти средние дают представление о том, как меняется в среднем у в зависимости от х. Поэтому группировка служит средством анализа связи в статистике. Но ряд групповых средних уx имеет тот недостаток, что он подвержен случайным колебаниям. Они создают колебания уx отражающие не закономерность данной зависимости.

Групповые средние хуже отражают закономерность связи, чем уравнение регрессии, но могут быть использованы в качестве основы для нахождения этого уравнения. Умножая численность каждой группы n_х на групповую среднюю у_х мы получим сумму у в пределах группы Суммируя эти суммы, найдем общую сумму у. Несколько сложнее с суммой ху. Если при сумме ху интервалы группировки малы, то можно считать значение x для всех единиц в рамках группы одинаковым У множив на него сумму у, получим сумму произведений x на у в рамках группы и, суммируя эти суммы, общую сумму xу. Численность nx, здесь играет такую же роль, как взвешивание в вычислении средних.

Множественная регрессия - регрессия между переменными у и x₁,x₂,…,x_m. Т. е. модель вида: у = f (x₁,x₂,…,x_m)+E, где у - зависимая переменная (результативный признак); x₁,x₂,…,x_m- независимые, объясняющие переменные (признак-фактор); Е- возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели.

Множественная регрессия применяется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах. Цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное воздействие на моделируемый показатель.

Основные типы функций, используемые при количественной оценке связей: линейная функция: у = а₀ + a₁х₁ + а₂х₂,+... + a_mx_m.

Параметры a_1, а_2, a_m, называются коэффициентами «чистой» регрессии и характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне;

нелинейные функции: у=ах₁^b1 х₂^b2.... x_m^bm- - степенная функция; b₁, b₂..... b_m - коэффициенты эластичности; показывают, насколько % изменится в среднем результат при изменении соответствующего фактора на 1 % и при неизменности действия других факторов.

- гипербола;

- экспонента.

Отбор факторов при построении множественной регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

3. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Методы построения уравнения множественной регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии к разным методам:

1) метод исключения (отсев факторов из полного его набора);

2) метод включения (дополнительное введение фактора);

3) шаговый регрессионный анализ (исключение ранее введенного фактора).

Оценка существенности связи

Проверка адекватности модели регрессии, построенной на основе того или иного уравнения связи, начинается с проверки значимости каждого коэффициента регрессии.

Оценка значимости коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:

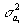где - дисперсия коэффициента регрессии.

Дисперсия коэффициента регрессии может определяться:

где - дисперсия результативного признака;

- число факторных признаков в уравнении.

При проверке адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:

1. Построенная модель на основе ее проверки по критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению прогнозов.

2. Модель по критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для прогнозов.

3. Модель по критерию Фишера адекватна, но все коэффициенты регрессии незначимы. Модель в этом случае отвергается. На ее основе никаких решений проводить нельзя.

Коэффициент детерминации показывает какая часть общей вариации зависимой переменной объясняется влиянием изменения факторного признака.

Линейный коэффициент корреляции изменяется в пределах от -1 до +1 и выражает характер связи: " чем ближе значение коэффициента к 1 (-1), тем теснее связь между признаками;

если r = 0, то связь отсутствует;

0<r<1— связь прямая и однонаправленная;

- 1 < r < 0 — связь обратная;

r= 1 (-1) — связь функциональная.

Непараметрические показатели связи

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи массовых процессов и явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного или нескольких факторов.

Для оценки тесноты и существенности связи между двумя коррелированными признаками используется линейный коэффициент корреляции.

Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Знаки коэффициентов регрессии и корреляции совпадают.

Ранговые коэффициенты связи

В анализе массовых процессов и явлений часто приходится прибегать к различным условным оценкам, которые называются рангами, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.

Ранг - порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые они определяют. Данные ранги называются связными.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается для случаев, когда нет связных рангов. Его формула:

где - квадрат разности рангов;

n - число наблюдений (число пар рангов).

Коэффициент Спирмена принимает любые значения в интервале (-1;1). Значимость коэффициента корреляции рангов Спирмена проверяется на основе критерия Стьюдента.

Расчет коэффициента Спирмена осуществляется по следующему алгоритму. Сначала ранжируются значения результирующего признака. Затем ранжируются значения факторного признака. Значения рангов парных признаков: результирующего и факторного сравниваются, вычисляется разница рангов, которая возводится в квадрат и далее подставляется в формулу.

Расчет данного коэффициента выполняется в следующей последовательности:

1) значения Х ранжируются в порядке возрастания или убывания;

2) значения У располагаются в порядке, соответствующем значениям Х;

3) для каждого ранга У определяется число следующих за ним рангов, превышающих его величину. Суммируя таким образом числа, определяется величина Р как мера соответствия последовательностей рангов Х и У и учитывается со знаком (+);

4) для каждого ранга У определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-);

5) определяется сумма баллов по всем членам ряда.

 

 

3. Перестрахование (англ. reinsurance) — система экономических страховых отношений между страховыми организациями (страховщиками) по поводу заключенных со страхователями договоров страхования. В соответствии с договором перестрахования страховщик, принимая на страхование риски, часть ответственности по ним передаёт на согласованных условиях другим страховщикам (перестраховщикам) с целью создания по возможности сбалансированного страхового портфеля, обеспечения финансовой устойчивости и рентабельности страховых операций. Перестрахование позволяет страховой компании принимать риски клиентов, которые были бы слишком велики для одного страховщика. Перестрахование называют также «вторичным» страхованием или страхованием страховщиков. Перестрахование происходит не только на уровне национальной экономики, оно уже стало международным видом страховой деятельности. В этой связи углубление специализации в страховом деле привело к формированию особой группы страховых компаний — перестраховщиков (англ. reinsurer), специализирующихся на операциях перестрахования.

 

Перестрахование является настолько специфической областью отношений по поводу страхования, что выработало свою терминологию. Наиболее распространенными терминами, применяемыми в перестраховании, являются следующие:

Перестрахователь — страховщик, принявший на страхование риски и передавший часть этих рисков вместе с частью страховой премии по этим рискам другому страховщику. Взамен он получил обязательство возмещения части расходов, вызванных наступившими по этим рискам страховым случаям. Перестрахователя называют также передающей компанией или цедентом. Перестраховщиком называют страховщика, принявшего в перестрахование риски. Перестраховщика называют также цессионарием или цессионером, а процесс передачи рисков в перестрахование — цессией (англ. cession). Приняв в перестрахование риск, перестраховщик может частично передать его другому страховщику (перестраховщику), который, в свою очередь, может передать его следующему страховщику (перестраховщику). Эта операция третичного и последующих размещений рисков получила название ретроцессия (англ. retrocession), а страховщик, принявший риски в порядке последующих за цессией размещения рисков получил название ретроцессионария или ретроцессионера. Перестраховщик, передающий риски в ретроцессию, называется ретроцедентом.

Существует большое количество разнообразных форм и методов перестрахования.

По форме способа передачи риска различают факультативное и облигаторное перестрахование.

При факультативном перестраховании перестрахователь отдает только те риски перестраховщику, которые считает необходимым для себя, и факультативный договор заключается в отношении одного конкретного договора страхования. При облигаторном подлежит перестрахованию портфель договоров определённого вида (все и каждый).

Oблигаторное перестрахование, в свою очередь, разделяют по способу распределения риска между цедентом и цессионарием на:

1. Пропорциональное перестрахование с двумя основными разновидностями: квотное (англ. quota share reinsurance) и эксцедентное (англ. surplus reinsurance).

2. Непропорциональное перестрахование с двумя основными разновидностями: на базе эксцедента убытка (англ. excess of loss) и на базе эксцедента убыточности (англ. stop loss)

 

Перестрахование как операция по достижению финансовой устойчивости страховщика

Необходимость перестрахования как системы перераспределения риска для обеспечения сбалансированности страхового портфеля. Перестрахование и сострахование.
Формы перестрахования: факультативное и облигаторное. Факультативно-облигаторное перестрахование. Предмет перестрахования и объём ответственности перестраховщика. Факторы, влияющие на размер собственного удержания. Оговорка об оригинальных условиях. Финансовые расчёты в перестраховании. Пропорциональное перестрахование: квотное и эксцедент сумм. Непропорциональное перестрахование: эксцедент убытка и эксцедент убыточности.
Значение перестрахования в развитии российского страхового рынка. Современное состояние перестраховочного рынка в России и за рубежом.
Основные понятия темы: цедент, цессионер, цессия, ретроцессия, ретроцедент, ретроцессионер, собственное удержание, эксцедент сумм, эксцедент убытков, эксцедент убыточности, факультативное перестрахование, облигаторное перестрахование.

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: