Элементарные задачи на построение.

Окружность.Круг.

Окружность -замкнутая плоская кривая, все точки которой одинаково удалены от предоставленной точки (центра), лежащей в той же плоскости, что и кривая. Еще круг можно найти как часть плоскости,ограниченную окружностью.

Отношение длины окружности к её диаметру идентично для всех окружностей. Это отношение и есть трансцендентное число, означаемое буквой греческого алфавита пи:π = 3.14159...

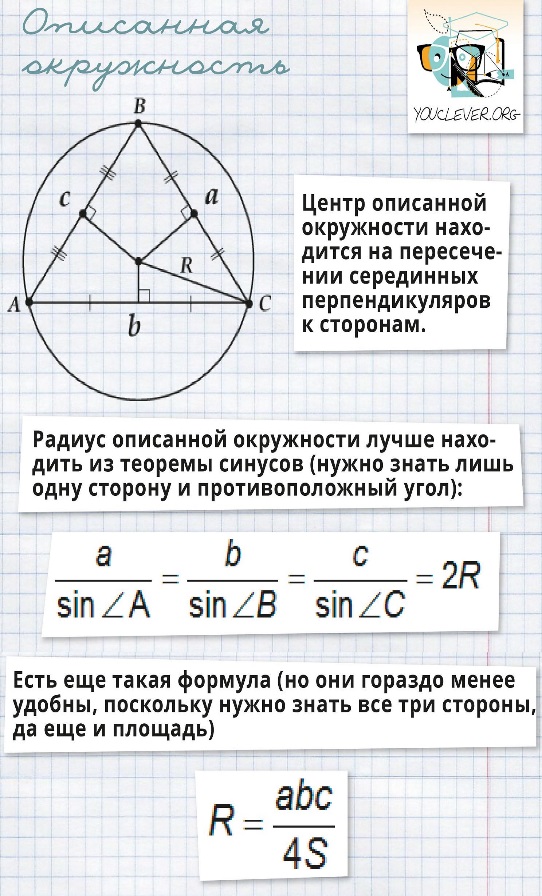
Длина окружности С=2ПR

Круг - геометрическое пространство точек плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит данного неотрицательного числа, именуемого радиусом круга.

Если радиус соответствует нулю, то круг становится точкой

Границей круга, сообразно определению, есть окружность.

При вращении плоскости относительно центра круг переходит сам в себя.

Круг является выпуклой фигурой.

Периметр круга (длина окружности, ограничивающей

круг) можно найти по формуле: 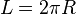где R – радиус круга.

Площадь круга где S - площадь круга,R - радиус круга,D - диаметр круга,

Радиус — 1) расстояние от центра круга до его границы; 2) отрезок, который соединяет центр круга с его границей.

Диаметр — 1) самое большое расстояние между точками границы круга; 2) отрезок, который соединяет две точки границы круга и содержащий его центр.

Сектор круга — пересечение круга и некоторого его центрального угла, т.е. часть круга, которая ограничена дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегмент — часть круга, ограниченная дугой и стягивающей ее хордой.

Элементарные задачи на построение.

Геометрические задачи на построение, возможно, самые древние математические задачи. Кому-то они сейчас могут показаться не очень интересными и нужными, какими-то надуманными. И в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный семнадцатиугольник или треугольник по трем высотам, или даже просто сделать построение параллельной прямой. Современные технические устройства сделают все эти построения и быстрее, и точнее, чем любой человек, а заодно смогут выполнить и такие построения, которые просто невозможно выполнить при помощи циркуля и линейки.И все же без задач на построение геометрия перестала бы быть геометрией. Геометрические построения являются весьма существенным элементом изучения геометрии.

В чем же особенность этих задач? Задачи на построение не просты. Не существует единого алгоритма для решения всех таких задач. Каждая из них по-своему уникальна, и каждая требует индивидуального подхода для решения. Именно поэтому научиться решать задачи на построение чрезвычайно трудно, а, порой, практически невозможно. Но эти задачи дают уникальный материал для индивидуального творческого поиска путей решения с помощью своей интуиции и подсознания.

Суть решения задачи на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру, если дана некоторая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры. Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи. Найти решение задачи на построение – значит свести ее к конечному числу основных построений, то есть указать конечную последовательность основных построений, после выполнения которых, искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии.

Еще в IV в. до н. э. древнегреческие геометры разработали общую схему решения задач на построение, которой мы пользуемся и теперь