Методические указания по выполнению контрольных работ

 

КОНТРОЛЬНАЯ РАБОТА №1

 

Тема 1. Прогнозирование

Прогнозирование – это вероятностное суждение о перспективах развития экономических показателей в будущем.

В логистике прогнозируются спрос, объёмы продаж, расход материальных ресурсов, уровень запасов и др. От точности и достоверности прогноза этих показателей зависит эффективность логистического менеджемента. Чаще всего прогноз названных показателей связывают исключительно со временем, предполагая, что через время учитывается влияние всех остальных факторов, таких как среднедушевой денежный доход, розничная цена, численность населения и проч.

Прогноз осуществляется на основе анализа тенденций развития. Под тенденцией понимают общее направление развития, которое называют «тренд ». Тренд характеризует основную закономерность изменения показателя во времени и определяется влиянием постоянно действующих факторов. Отклонения от тренда объясняются наличием случайных факторов. Выявленный тренд является моделью для прогнозирования.

При прогнозировании чаще других используются методы экстраполяции, т.е. распространения прошлых закономерностей на будущее. В этом случае исходная информация имеет вид динамического (временного) ряда. Динамический ряд – это упорядоченная совокупность значений показателя y за n предшествующих последовательных периодов времени t: y_t = (y ₁, y ₂, …, y _n). По этим данным выполняется прогноз при условии, что процесс развития в будущем не претерпит существенных изменений, то есть будет эволюционным.

Данные динамического ряда образуют так называемую базовую линию,поскольку прогноз базируется на этих данных. Длина базовой линии n – количество наблюдаемых значений показателя у. Глубина прогноза m – это количество прогнозируемых значений. Глубина прогноза m должна быть значительно меньше длины базовой линии n.

Для выявления тренда часто используют так называемые регрессионные модели прогноза, которые представляет собой уравнения вида:

= f(t) + ɛ_t,

где f(t) –функция, описывающая тренд, ɛ_t – случайная составляющая.

Наиболее простой и употребляемой моделью является уравнение линейной регрессии, когда в качестве тренда используется линейная функция f(t)= a_*t + b. На графике линейная функция изображается в виде прямой линии, которая называется «прямая регрессии».

Параметры прямой регрессии a и b выбираются так, чтобы уравнение линейной регрессии наилучшим образом было приближено к базовым данным у_t. Обычно наилучшее приближение определяется по методу наименьших квадратов (МНК): должна быть наименьшей сумма квадратов отклонений базовых значений у_t от соответствующих значений f(t), посчитанных по уравнению регрессии.

В соответствии с этим требованием для вычисления параметров a и b

линейной регрессии получены формулы:

 

;

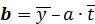
После нахождения уравнения линейной регрессии:

≈ а _* t + b,

оценивают его адекватность, то есть насколько хорошо оно аппроксимирует (описывает) базовые данные. Для этого применяют различные способы. Один из них основан на нахождении средней ошибки аппроксимации. Если эта ошибка невелика, то полученное линейное уравнение регрессии используют для прогнозирования.

Однако найденное уравнение тренда характеризует лишь средний уровень динамики ряда. Возникает необходимость оценить ошибку прогноза при определённом уровне доверия, задаваемом вероятностью р. Обычно эти вероятности берут высокими: 90%, 95% или 99%. В результате указывают доверительный интервал для прогноза с данной надёжностью р.

 

 

Задача 1–10. Известны данные об уровне продаж некоторого товара у_t в тыс. руб. за десять месяцев текущего года.

1) Изобразить эти данные графически.

2) Построить линейную регрессионную модель для прогнозирования.

3)Оценить адекватность модели с помощью средней ошибки аппроксимации.

4) Сделать прогноз продаж на два последующих месяца.

5) Найти ошибку прогноза при уровне надежности р = 90%.

6) Указать относительную точность прогноза и доверительный интервал прогноза для каждого из прогнозных месяцев.

 

у_t = (65; 66; 69; 72; 73; 71; 76; 78; 77; 78).

Решение

1)Данныезначения для месячного уровня продаж у_t образуют базовую линию, длины n =10. Для наглядности, изобразим данные задачи графически: на горизонтальной оси будем откладывать время t от 0 до 10, а на вертикальной оси уровни продаж у_t от 65 до 78. Для удобства построения вертикальную ось можно «разорвать».

 

 

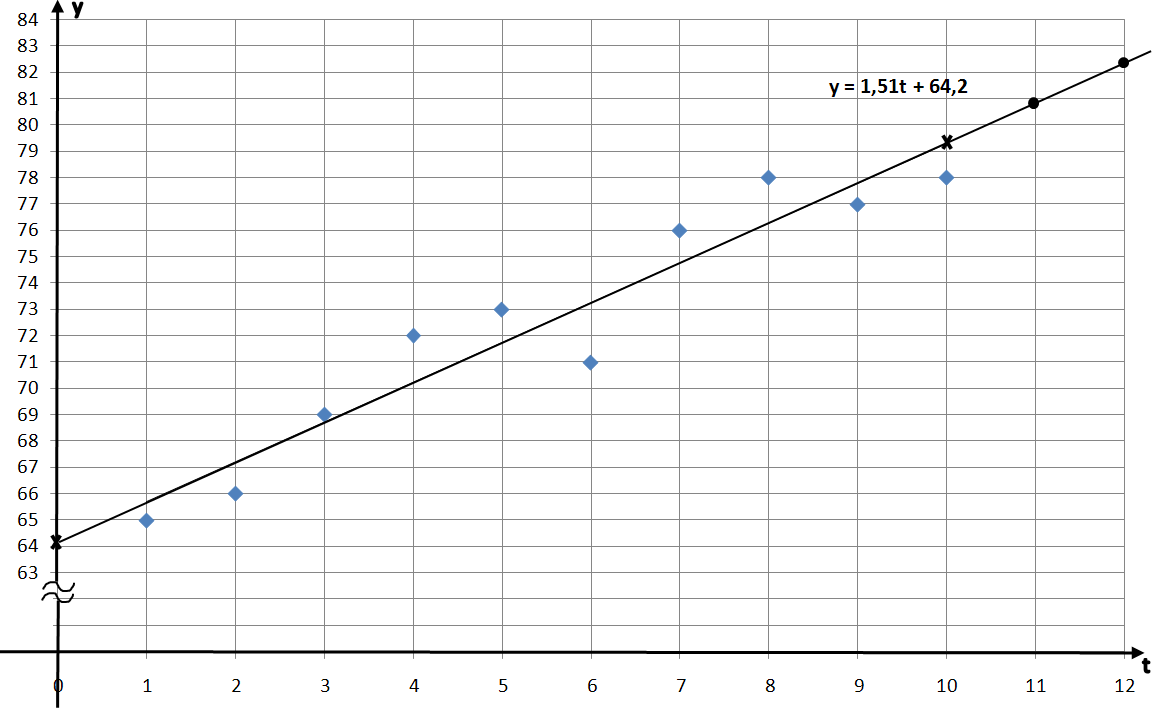
Расположение точек на графике показывает, что они приблизительно выстраиваются вдоль некоторой прямой линии, что даёт возможность сделать предположение о линейной зависимости уровня продаж у_t от времени t: у_t = а _* t + b.

2) Для вычисления значений параметров уравнения регрессии a и b по формулам, указанным ранее, удобно построить расчётную таблицу. В первой колонке этой таблицы помещают время t, это порядковый номер месяцев от 1 до 10. Вторая колонка содержит соответственные значения базовых данных у_t. В третьей колонке расположены значения квадратов времени t ², а в четвёртой произведения соответственных значений t _* у_t. Внизу найдены суммы для первых четырёх колонок. С их помощью вычисляем все средние значения, необходимые для нахождения параметров a и b.

Остальные колонки расчётной таблицы будут заполняться позже.

 

	t	уt	t2	t* уt	f(t)	│‌‌уt – f(t) │	Отнош.	(уt – f(t))2
					65,71	0,71	0,011	0,50
					67,22	1,22	0,018	1,48
					68,73	0,27	0,004	0,07
					70,24	1,76	0,024	3,11
					71,75	1,25	0,017	1,57
					73,25	2,25	0,032	5,06
					74,76	1,24	0,016	1,53
					76,27	1,73	0,022	2,95
					77,78	0,78	0,010	0,61
					79,29	1,29	0,017	1,67
∑				4 112			0,172	18,62

 

Найдём все средние значения:

= ∑ t / n = 55/10 = 5,5; = ∑ y _t/ n = 725/10 = 72,5;

= ∑ t ²/ n = 385/10 = 38,5; _.= (∑ t _* у _t)/ n = 4112/10 = 411,2.

Вычислим параметры уравнения регрессии, по формулам указанным выше:

= =1,51;

= 72,5 – 1,51_*5,5 = 64,2.

В результате получим уравнение линейной регрессии:

f(t) = 1,51_* t +64,2.

Построим на графике найденное уравнение прямой по двум точкам:

при t = 0, f(0) = 11,51*0 + 64,2 = 64,2; это точка (0; 64,2);

при t = 10, f(10) = 1,51*10 + 64,2 = 15,1 + 64,2 = 79,3; это точка (10; 79,3). Отметим эти точки на графике (они отмечены крестиками) и проведём через них прямую линию. Это и есть прямая регрессии. Наблюдаемые точки (t; y _t) лежат по обе стороны от прямой регрессии и в совокупности наилучшим образом приближены к ней. Обратите внимание, что точка с координатами ( , обязательно должна лежать на прямой регрессии. В рассматриваемой задаче это точка (5,5; 72,5), она действительно лежит на прямой.

 

3) Оценим адекватность полученной модели, то есть насколько хорошо регрессионные значения f(t) приближены к данным фактическим значениям у _t.. Это можно сделать с помощью характеристики, называемой «средняя ошибка аппроксимации». Она ‌‌вычисляется по формуле:

А = (1/ n) ∑(‌‌‌│ у _t – f(t) │/ y _t).

Чем меньше средняя ошибка аппроксимации, тем выше качество регрессионной модели. Допустимый предел ошибки не более 10%.

‌ Используя найденное уравнение регрессии, вычислим значения у для всех значений t от 1 до 10: f(1) =1,51_*1+64,2 = 65,71; f(2) =1,51_*2+64,2 = 67,22 и т. д. Поместим эти значения в пятую колонку расчетной таблицы под заголовком f(t). Следующая шестая колонка содержит отклонения данных значений y_t от значений, вычисленных по уравнению регрессии f(t), взятые по абсолютной величине: │ у _t – f(t) │. В следующей седьмой колонке вычислим отношения найденных отклонений к соответствующим фактическим значениям y_t: │ у _t – f(t) │/ y _t. Далеенайдём итоговую сумму этих отношений. Полученное значение суммы делим на объём выборки n = 10. Найденное значение и есть ошибка аппроксимации. В решаемой задаче А = = 0,172/10 = 0,0172, то есть А = 1,72%. Ошибка значительно меньше допустимого значения 10%, следовательно найденная регрессионная модель адекватна и её можно использовать для прогнозирования.

4) Сделаем прогноз на следующие два месяца одиннадцатый и двенадцатый:

у ₁₁ = f (11) = 1,51_*11 + 64,2 = 80,80;

у ₁₂ = f (12) = 1,51_*12 + 64,2 = 82,31.

На графике эти значения отмечены жирными точками на прямой регрессии, они соответствуют значениям времени t =11 и t =12.

5) Найденные прогнозные значения являются усреднёнными. В действительности можно прогнозировать лишь попадание прогнозных значений в некоторый доверительный интервал. Уровень доверия по условию задачи равен 90%.

Ошибка прогноза Δ вычисляется по формуле: Δ = _*T_*K_m, где

– остаточное среднее квадратическое отклонение,

Т– квантиль распределения Стьюдента,

К _m – поправочный коэффициент, m = 1;2.

Для подсчёта остаточного среднего квадратического отклонения S _y заполним последнюю колонку расчётной таблицы. Для этого возводим в квадрат найденные ранее отклонения (в шестой колонке) и суммируем эти квадраты отклонений. Полученную сумму делим на число степеней свободы (n – k) = 10 – 2 = 8, где n =10 – длина базового периода, k =2 – количество параметров регрессионной модели (их два a и b). Остаточное среднее квадратическое отклонение вычисляется по формуле:

В рассматриваемой задаче:

Квантиль Т находится по таблице распределения Стьюдента. Он зависит от уровня надёжности р и числа степеней свободы (n – k).

Если р = 90%, а число степеней свободы n – k = 10-2= 8, то Т=1,86.

Поправочный коэффициент К_m вычисляется по специальной формуле и зависит от длины базового периода n и от глубины прогноза m.

Глубина прогноза отсчитывается, начиная от базового периода, длина которого n =10. Для прогноза на 11-ый месяц глубина m = 1 и поправочный коэффициент К₁ = 1,21. Для прогноза на 12-ый месяц глубина m = 2 и поправочный коэффициент К₂ = 1,27.

В результате получим следующие ошибки прогноза на 11-ый и 12-ый месяцы: Δ₁₁ = 1,53*1,86*1,21 = 3,44; Δ₁₂ = 1,53*1,86*1,27 = 3,60.

При увеличении глубины прогноза ошибка прогноза возрастает, поэтому прогноз выполняют на глубину не более четверти длины базового периода, то есть менее чем n /4.

6) Найдём относительную погрешность прогноза: δ_t = ( / y_t)_*100%. Если относительная ошибка не более 10%, то точность прогноза высокая, если от 10% до 20%, то точность хорошая; если от 20% до 50%, то точность удовлетворительная, иначе точность неудовлетворительная.

В данной задаче δ₁₁ = Δ₁₁ / у ₁₁ = 3,44/80,80 = 0,0425, т. е. 4,25%,

δ₁₂ = Δ₁₂ / у ₁₂ = 3,60/82,31 = 0,0438, т. е. 4,38%,

это означает, что точность прогноза высокая.

Результаты прогноза записывают в виде доверительного интервала:

y _t. Є (f(t) – ; f(t) _.+ ) с вероятностью р; t =11 и t = 12. Чем выше вероятность р, тем шире интервал для прогнозирования и, следовательно, точность хуже.

В решаемой задаче с вероятностью 90%:

у ₁₁Є (80,80 – 3,44; 80,80 + 3,44) = (77,36; 84,24),

у ₁₂Є (82,31 – 3,60; 82,31 + 3,60) = (78,71; 85,91).

Ответ. Линейная трендовая модель для прогнозирования имеет вид:

y = 1,51_* t +64,2.

Прогноз продаж на 11-ый месяц: 80,80 ± 3,44; на 12-ый месяц: 82,31 ± 3,60

с надёжностью 90%. Модель адекватная, точность прогноза высокая.

 

 

Тема 2. Системы массового обслуживания (СМО)

СМО – это системы, где многократно повторяются одни и те же однотипные процессы, связанные с обслуживанием (склады, магазины, автозаправки, ремонтные мастерские, телефонные сети и т. п.). Основные составляющие СМО: канал обслуживания (грузчик, кассир, ремонтная бригада, телефонный аппарат и т. п.) и поток требований или заявок (покупатели, клиенты, абоненты и проч.).

Канал обслуживания характеризуется двумя параметрами: t _{обсл .}– среднее время обслуживания одного требования одним каналом; μ – интенсивность обслуживания, это количество требований, обслуживаемых одним каналом в ед. времени. Связь между ними: μ = 1/ t _{обсл .}; t _{обсл .}=1/ μ.

Требования (заявки) характеризуются также двумя параметрами: Т – среднее время между двумя последовательными заявками; λ – интенсивность поступления заявок, это количество заявок, поступающих в ед. времени. Связь между ними: λ = 1/Т; Т = 1/ λ.

Параметр загрузки ρ = λ/μ – важнейшая характеристика СМО, показывает соотношение интенсивности поступления требований с интенсивностью их обслуживания.

СМО может иметь несколько каналов обслуживания. Обычно считают, что интенсивность обслуживания у них одинаковая. По количеству каналов различают:

– одноканальные СМО, имеющие один канал обслуживания (n =1);

– многоканальные СМО, когда каналов обслуживания два и более (n ≥2).

По наличию очереди различают следующие виды СМО: с отказом (без очереди); с ожиданием (очередь неограниченная); смешанного типа (очередь ограничена).

В дальнейшем будут рассматриваться системы Марковского типа. Отличительным свойством таких систем является отсутствие последействия: будущее системы зависит только от её состояния в данный момент и не зависит от того, что было до этого момента. Поток заявок при этом называется простейшим. Для систем такого типа имеются математические модели, одной из которых мы и воспользуемся ниже для решения задачи.

 

Задача 11–21. Отгрузка производится со склада имеющего n погрузочных площадок. На склад для погрузки поступает простейший поток грузовиков с интенсивностью λ машин в час. Среднее время погрузки одной машины составляет t_обсл минут. Если все погрузочные площадки заняты, то грузовики становятся в очередь.

n = 4; λ = 9 маш./час; t_обсл. = 24 мин.; к =2.

1) Укажите вид системы обслуживания.

2) Определите интенсивность обслуживания и параметр загрузки системы.

3) Сколько погрузочных площадок должен иметь склад, чтобы очередь не была бесконечной? Выполняется ли это условие для данной СМО?

4) Перечислите возможные состояния СМО и найдите соответствующие им вероятности.

5) Найдите вероятность того, что очереди нет.

6) Какова вероятность наличия очереди?

7) Какова вероятность того, что в очереди не более «k» грузовиков? Более чем «k» грузовиков?

8) Найдите среднее количество грузовиков в очереди.

9) Каково среднее число грузовиков на обслуживании?

10) Каково среднее число грузовиков на складе?

11) Укажите среднее время пребывания грузовика в очереди.

12) Найдите среднее время пребывания грузовика на складе.

Оцените работу склада с помощью показателей эффективности, найденных в пунктах 5 – 12.

 

Решение

1) Имеем четырёхканальную СМО с неограниченной очередью. Здесь каналами обслуживания являются разгрузочные площадки, их 4, а поток заявок (требований) образуют прибывающие на погрузку грузовики.

2) Найдём интенсивность обслуживания μ и параметр загрузки системы ρ:

μ = 1/t_обсл = 1/24 маш./мин. = (1/24)*60 маш./час. = 2,5 маш./час.

ρ = λ /μ = 9/2,5 =3,6.

3) Чтобы очередь не была бесконечной, нужно чтобы интенсивность поступления требований λ была меньше общей интенсивности обслуживания всех n каналов: λ ˂ n _*μ или λ /μ ˂ n. Таким образом, должно выполняться условие: ρ ˂ n. В решаемой задаче это условие выполняется, так как ρ = 3,6, а n =4.

4) Возможные состояния четырехканальной СМО с неограниченной очередью:

S₀ – все каналы обслуживания свободны, очереди нет;

S₁– 1 канал занят, остальные 3 канала свободны, очереди нет;

S₂ – 2 канала заняты, остальные 2 канала свободны, очереди нет;

S₃ – 3 канала заняты, 1 канал свободен, очереди нет;

S₄ – все 4 канала заняты, очереди нет;

S₅ = S₄₊₁ – все 4 канала заняты, и 1 заявка в очереди;

S₆ = S₄₊₂ – все 4 канала заняты, и 2 заявки в очереди;

S₇ = S₄₊₃ – все 4 канала заняты, и 3 заявки в очереди;

…………………………………………………………

Найдём вероятности этих состояний, используя следующие формулы:

Подставив в эти формулы, данные для решаемой задачи, получим:

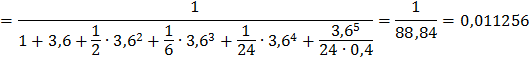
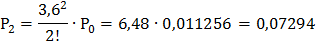
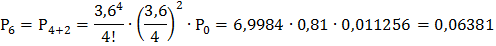
и т.д. Очевидно, что сумма всех вероятностей единица: Р₀+ Р₁+ Р₂+ … = 1.

 

5) Событие «очереди нет» соответствует состояниям: S₀, S₁, S₂, S₃, S₄. Складывая вероятности, соответствующие этим состояниям, получим:

Р* = Р (очереди нет) = Р₀+Р₁+ Р₂+ Р₃+ Р₄ = 0,011256 + 0,04052 + 0,07294 +

+ 0,08753 + 0,07878 ≈ 0,291 (29,1%).

6) Найдём вероятность наличия очереди. Очевидно, что

Р(очередь есть) = 1 – Р(очереди нет) = 1 – Р* = 1 – 0,291 = 0,709 (70,9%).

7) Вероятность того, что в очереди не более 2-х грузовиков, равна:

Р(не более 2-х груз. в очереди) = Р(к ≤ 2) = Р₀ + Р₁ + Р₂ + Р₃ + Р₄ + Р₅ + Р₆ =

= 0,011256+ 0,04052+ 0,07294+ 0,08753+ 0,07878+ 0,07090+ 0,06381 ≈ 0,4257.

Тогда вероятность того, что в очереди более чем 2 грузовика, составит:

Р(более 2-х груз. в очереди) = Р(к ˃2) = 1 – Р(к ≤ 2) =

= 1 – 0,4257 = 0,5743 (57,43%).

8) Среднее количество грузовиков в очереди называется также средней длиной очереди и находится по формуле:

9) Среднее количество грузовиков на обслуживании L_обсл. находим как математическое ожидание числа грузовиков находящихся на обслуживании, а именно для каждого состояния умножаем число занятых обслуживанием каналов на вероятность состояния. Следует заметить, что на обслуживании будет 4 грузовика, начиная с состояния S ₄ и вероятность этого равна: Р ₄ + Р ₅ + Р ₆ + … = 1 – Р ₀ – Р ₁ – Р ₂ – Р ₃ = 1– 0,011256 – 0,04052 – 0,07294 – 0,08753 ≈

= 1 – 0,21225 = 0,78775.

Тогда L_обсл. = 0_*Р ₀ + 1_*Р ₁ + 2_*Р ₂ + 3_*Р ₃ + 4_*(1 – Р ₀ – Р ₁ – Р ₂ – Р ₃) =

= 0*0,011256 +1*0,04052 +2*0,07294 +3*0,08753 + 4*0,78775 = 3,6.

10) Среднее количество грузовиков в системе складывается из количества грузовиков на обслуживании плюс количество грузовиков в очереди:

L_{сист .}= L_обсл + L_оч. = 3,6 + 7,1 = 10,7.

11) Среднее время пребывания грузовика в очереди находим по формуле:

Т_оч. = L_оч. /λ = 7,1 /9≈0,79 час. = 0,79*60 ≈ 47,4 мин.

12) Аналогично находим среднее время пребывания грузовика на складе:

Т_сист. = L_сист. /λ = 10,7 /9≈1,19 час. = 1,19*60 ≈ 71,4 мин.

 

Контроль. Должно выполняться условие: Т_сист. = Т_оч. + t_обсл.

Действительно Т_оч. + t_обсл. = 47,4 мин. + 24 мин. =71,4 мин. = Т_сист.

Оценим работу склада с помощью показателей эффективности, найденных в пунктах 5 – 12.

Система достаточно сильно загружена. Из четырёх погрузочных площадок в среднем заняты 3,6 площадки. Коэффициент загрузки системы высокий:L_обсл/n= 3,6/4 = 0,9, то есть на 90% система загружена. Большой процент грузовиков находится в очереди (70,9%). Достаточно большое количество грузовиков (в среднем 10,7) находятся на складе из них приблизительно 4 грузовика на обслуживании и приблизительно 7 грузовиков в очереди, где они ожидают погрузки в среднем 47,4 мин.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: