 |
Меры безопасности барьера с максимальным количеством баллов.
|
|
|
|
| Описание | Применение / комментарии | Кол-во баллов |
| Пожарная стена | Предохраняет распространение огня в другие места, по крайней мере, в течение 60 минут | |
| Обваловка (сборные пруды) | Сборные пруды, способные задержать наиболее крупные объемы возможных утечек (сбросов). | |
| Резервуар для воды | Достаточный объем воды для тушения огня в случае наиболее крупных утечек (выброса). | |
| Дисковое отключение при неполадке | Выпускает излишнее давление в атмосферу | |
| Аварийный выпускной клапан | Выпускает излишнее давление в атмосферу | |
| Аварийная сигнализация с автоприводом | Автозапуск инициирует эффективные меры безопасности | |
| Аварийный прерыватель | Прерывает автоматически, является составной частью защиты установки при отказе. | |
| Аварийная сигнализация с ручным управлением | Тревожная сигнализация подает сигнал оператору, постоянно находящемуся в операционном зале, и оператор предпринимает соответствующие защитные меры. | |
| Регулярный осмотр | Осмотр на 100% выполняется квалифицированным сотрудником при тщательном контроле качества. Интервалы между осмотрами зависят от вида оборудования. | |
| Нереверсивный вентиль | Обеспечивает движение потока в трубе в одном направлении. |
При построении барьерной диаграммы на каждой барьерной диаграмме можно отразить от 5 от 8 причин и последствий аварийной ситуации. Если насчитывается большее число причин, то потребуется построение более чем одной барьерной диаграммы. Если требуется построение более чем одной барьерной диаграммы, сделайте так, чтобы содержание каждой схемы являлось логическим продолжением каждой из них, так чтобы последовательности, имеющие общие барьеры были отражены на той же диаграмме. Графические схемы строятся так, чтобы обстоятельства, которые приводят к аварийной однотипной ситуации, были сгруппированы вместе.
|
|
|
Барьерные диаграммы могут быть использованы для получения общего представления о том, какая последовательность событий может ожидаться наиболее часто, или какие из них, могут привести к наиболее серьезным последствиям. Данный обзорный анализ, в свою очередь, может быть использован для выявления тех цепочек событий, в которых требуются дополнительные меры безопасности [8].
· Метод Монте-Карло
Методы создания математических моделей объектов и систем, а также имитационных моделей предполагают детерминированные задачи или задачи, решаемые в условиях неопределенности. Во втором случае неопределенные факторы или параметры, входящие в задачу, являются случайными величинами, вероятностные характеристики которых или известны или могут быть определены из опыта.
В реальных случаях приходиться анализировать безопасность сложных объектов и систем, в которых взаимосвязаны большое количество элементов и процессов (машина, агрегаты, организации, люди) и присутствует много случайных факторов, которые взаимно влияют друг на друга. В таких ситуациях единственным методом решения задачи является использование универсального метода статистического моделирования, называемого методом Монте-Карло.
Суть метода моделирования Монте-Карло состоит в том, что вместо того, чтобы пытаться описывать процесс с помощью каких-либо уравнений, которые могут быть чрезвычайно сложными и описывать процесс очень приближенно, производится модельное появление случайного события с помощью специально организованной процедуры.
Процедура предполагает получение случайных чисел, отождествляемых с каким-либо событием. Случайные числа могут быть связаны с вероятностью наступления неблагоприятного события (авария, взрыв, травма, выброс токсичных веществ и др.). По процедуре формирования случайного сигнала (цифры) происходит формирование переменной по ее распределению. Однако реализация, т.е. одно выпадение случайного числа не может служить характеристикой поведения системы, но при достаточно большом количестве реализаций этот выбор случайных чисел может быть обработан методами математической статистики, что дает вероятностные характеристики состояния и развития исходного объекта.
|
|
|
Блок-схема, представленная на рисунке, отражает укрупненную схему работы с моделью (рис. 3.16).

Рис.3.16 Схема работы с моделью имитационного моделирования
Анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой «воссоединение» методов анализа чувствительности и анализа сценариев на базе теории вероятностей.
Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов.
Для использования метода Монте-Карло необходимо представлять, хотя бы примерно, закон распределения. На практике в большинстве случаев описывают процессы и явления, имеющие нормальный закон распределения. Для получения случайных реализаций используют или готовые таблицы случайных чисел, или с помощью ЭВМ, используя генераторы (датчики) случайных чисел. При других законах распределения (биноминальное, экспоненциальное) вводят специальную программу формирования случайного сигнала по этому закону.
Метод статистического моделирования (метод Монте-Карло) имеет свои достоинства и недостатки.
Достоинства:
- возможность моделирования сложных систем, где действует много взаимодействующих случайных факторов;
- возможность проверки правильности других аналитических моделей;
- не требует серьезных упрощений и допущений, так как в статистическую модель можно заложить любые законы распределения, любой сложности системы.
Недостатки:
- громоздкость и трудоемкость в разработке, потребность в большом количестве расчетов для получения статистически достоверных данных;
- результаты статистического моделирования труднее воспринимать и осмыслить, чем аналитические модели и, кроме того, значительно труднее решать задачу оптимизации.
|
|
|
При статистических модельных исследованиях и разработке моделей с использованием метода Монте-Карло, базируясь на имеющейся статистике и предыдущем опыте, предполагается, что закон распределения в определенной мере известен. По этому закону производится генерирование случайных сигналов. Это производится в тех случаях, когда случайные явления обладают статистической устойчивостью, когда при достаточном повторении опытов, частота появления случайных событий стабилизируется и приближается к ее вероятности. Такие случайные параметры или факторы можно назвать доброкачественной статистической неопределенностью. Примером доброкачественной неопределенности являются отказы различных устройств, разрушение элементов конструкций за счет износа или усталости материалов. Эти примеры находятся в компетенции теории надежности. Но в системах «человек-машина-среда» могут быть неопределенности такого вида, когда мы не можем хоть как-то прогнозировать закон распределения случайных величин. Это могут быть неправильные и ошибочные действия оператора. В этих случаях при разработке моделей необходимо исходить из возможности возникновения самого наихудшего случая.
· Теория орграфов
Для анализа больших систем используются модели, представляющие собой процесс появления отдельных предпосылок и развития их в причинную цепь происшествия в виде соответствующих диаграмм причинно-следственных связей.
Орграф представляет собой набор вершин, определенные пары которых соединены линиями со стрелками или без стрелок.
Рассмотрим на примере: численность населения города влияет на количество мусора в нем. Мусор, в свою очередь, увеличивает бактериологическую зараженность, которая влияет на заболеваемость в городе, что приводит к изменению заболеваемости и смертности населения. Условия жизни в городе определяют сальдо миграции. Все это определяет нагрузку на очистные сооружения и может быть описано орграфом, изображенным на рис. 3.17.
|
|
|
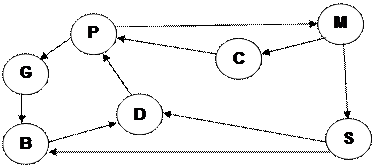 |
Рис. 3.17 Модельный орграф удаления мусора в городе
Р - Число жителей города
M - Условия жизни в городе
C - Миграция в город
G - Количество мусора на единицу площади
D - Число заболеваний
S - Число очистных сооружений
B - Бактериологическая зараженность на единицу площаlи
Орграфы (или диаграммы влияния) используются в настоящее время в различных модификациях, например:
· потоковые графы (графы состояний и переходов);
· ориентированные графы
· деревья происшествий («отказов»);
· деревья событий, деревья решений;
· функциональные сети различного предназначения и структуры, в т.ч.стохастической.
Основными компонентами диаграммы влияния служат узлы (вершины) и связи (отношения). В качестве узлов обычно подразумеваются простейшие элементы моделируемых категорий (события, состояния, свойства), а в качестве связей – действия, ресурсы и т.п.
Каждые два соединенных между собой узла образуют ветвь диаграммы. Отношения или связи между переменными или константами в узлах диаграммы представляются в виде дуг или ребер.
Узлы диаграммы характеризуются наборами данных, т.е. множеством выходов (значений, принимаемых переменными). Если диаграмма стохастическая, то дугам или ребрам приписываются вероятности (или распределения вероятностей) появления этих значений.
Диаграммы влияния сравнительно легко комбинируются с другими средствами формализации и моделирования. В последнее время к ним все чаще обращаются для решения задач повышение безопасности с помощью математического моделирования.
Так, с помощью предварительно построенных диаграмм – графов, сетей, деревьев могут быть получены математические модели аварийности и травматизма.
Дугой в орграфе называется ориентированная пара вершин графа (рис. 3.18).
 |
Рис.3.18 Дуга (Еi Ej)
Кратными дугами называются дуги, у которых совпадают начальная и конечная вершины (рис. 3.19).
 |
Рис. 3.19 Кратные дуги
Ребром называется неориентированная пара вершин (рис.3.20)
 |
Рис. 3.20 Ребро
Ребра и дуги называются смежными, если они имеют хотя бы одну смежную вершину. Ребра или одинаково направленные дуги называются кратными, если их концевые вершины совпадают.
Возникновение происшествий в системах техносферы и ликвидация их последствий могут быть представлены в виде следующего потокового графа (рис.3.21).

Рис.3.21 Потоковый граф
Здесь рассматриваемый процесс характеризуется шестью состояниями (безопасное, опасное, предаварийное, послеаварийное, состояние системы после смертельного несчастного случая и ее состояние после катастрофы), а также девятью переходами с соответствующими вероятностями. Для описания такого графа введения следующая формальная запись:
|
|
|
U = {1. 2. 3. 4. 5. 6} - множество узлов или вершин диаграммы;
V = {вышеприведенные наименования соотношений} - множество переменных, или соответствующих;
Д = {1-2, 2-1, 2-3, 3-2, 3-1, 3-4, 3-5, 3-6, 4-1} - множество дуг (ребер), соединяющих узлы;
Р = {Р12, Р21,Р23, Р32,Р31,Р34,Р35,Р36,Р41} - вектор мер возможностей перехода из узла I в узел j.
Полученная модель показывает воздействие одного показателя (в вершине графа) на другой показатель (вершину). Построенная модель позволяет провести анализ взаимодействия показателей, выявить показатели, связанные контуром (это очень важно при исследовании графов), определить начальные и конечные вершины. Но для моделирования развития систем этого недостаточно. Можно дополнить орграф, присвоив каждой дуге знак + (если при увеличении показателя i показатель j будет увеличиваться) или - (если при увеличении показателя i показатель j будет уменьшаться). Таким образом, мы получаем знаковый орграф (3.22).

Рис. 3.22 Ориентированный граф
Дуга (Р, G) имеет знак плюс, поскольку рост городского населения ведет, при прочих равных условиях, к увеличению количества мусора. Дуга (D, Р) имеет знак минус, так как рост заболеваемости ведет к уменьшению численности населения, а уменьшение заболеваемости — к увеличению. Дуга (Р, М) имеет знак плюс, так как рост населения ведет к улучшению инфраструктуры города, т. е. к улучшению условий жизни. Дуга (М, С) имеет знак плюс, так как улучшение условий жизни увеличивает миграцию населения в город, что, в свою очередь, ведет к росту населения — дуга (С, Р). Улучшение условий жизни в городе ведет к увеличению числа очистных сооружений — дуга (М, S) и т.д.
Модели, основанные на знаковых орграфах, являются весьма упрощенными. В реальных системах воздействие некоторых переменных на другие может быть разной силы, тогда как модель, основанная на знаковом орграфе, предполагает одинаковое по силе воздействие по всем дугам, отличающееся только знаком. Чтобы усилить модель, каждой дуге, кроме знака, можно присвоить еще и вес. Тогда мы получим взвешенный орграф, который является более тонким инструментом моделирования.
Определение весов дуг орграфа может быть проведено так же, как и знаков, на основе логики и экспертных оценок. В случае, когда имеется статистическая информация, весовые коэффициенты могут быть установлены на основе обработки этой информации.
Модель, базирующуюся на орграфах, можно сделать еще более глубокой по содержанию и точности описания, если построить функциональные орграфы.
В ориентированном графе (рис. 16) связи между вершинами заданы дугами, в неориентированном – ребрами. Граф является смешанным если в него входят и дуги, и ребра.
Путем в графе называется такая конечная последовательность дуг, в которой начало каждой последующей дуги совпадает с концом предыдущей. Например, путь, {(2,4)(4,5)(5,7)(7,10)(10,12)} можно записать в виде последовательности вершин {2,4,5,7,10,12}. Для неориентированного графа путь называется цепью.
Контуром называется путь, начальная вершина которого совпадает с конечной. Длина пути или контура определяется числом входящих в него дуг.
Полученная с помощью орграфа модель отражает воздействие одной вершины на другую. Дуги орграфа отражают характер взаимодействия. В зависимости от способа задания дуг различают следующие виды орграфов:
Взвешенный орграф – взаимодействие вершин в нем отражено только качественно. Для количественного описания модели дугам присваиваются весовые коэффициенты, отражающие степень влияния одной вершины на другую. Орграф, дугам которого присвоены весовые коэффициенты, называется взвешенным орграфом.
В функциональном орграфе дугам ставится в соответствие вместо знака или весового коэффициента функциональная зависимость.
Вероятностный орграф – орграф, имеющий случайные возмущения при взаимодействии вершин (дугам ставится математическое ожидание случайной величины).
Гибридные орграфы. В ряде случае оказывается целесообразным сочетать взвешенный и функциональный орграфы. Обычно это происходит при недостатке информации или при невозможности экспертов отразить зависимость изменения одного показателя от другого. В этих случаях орграфы имеют дуги, части которых поставлены в соответствие функциональные зависимости, а части - весовые коэффициенты. Такие орграфы называют гибридными.
Динамические орграфы. В динамических орграфах значения весов для некоторых (или всех) дуг не остаются постоянными, а зависят от величин показателей в вершинах орграфа, что позволяет повысить гибкость взвешенных орграфов. В этом случае весовой коэффициент дуги ij может быть записан в виде зависимости от некоторого показателя.
При исследовании реальных систем важен учет времени реализации воздействия одного показателя на другой или о времени реакции одного показателя на изменения другого.
Простейший подход, который позволяет учесть временные задержки импульсного процесса - установка дополнительных промежуточных вершин. Например, если показатель j реагирует на изменение показателя i через одну временную единицу, а показатель l реагирует на изменение показателя i через три временных единицы, то орграф с временными задержками примет вид, который показан на рис. 3.23.
 |
Рис. 3.23 Импульс передается от вершины 1 к вершине 2 с задержкой в 3 единицы
Недостатком данного подхода является то, что количество вершин орграфа увеличивается, орграф становится громоздким и трудоемкость расчетов увеличивается.
Вершины орграфа составляют сложный контур, который может быть представлен отдельными простыми контурами. Среди них можно выделить контуры, все дуги которых имеют знак «плюс». При росте значания одной из вершин в этом контуре, значения всех остальных вершин (а также и этой) будут возрастать. Очевидно, что отклонение в такой контуре будет все время усиливаться.
Контуры, усиливающие отклонения, называются контурами положительной обратной связи.
Контур, содержащий одну отрицательную дугу, противодействует росту отклонения, так как рост значения одной из вершин приводит к уменьшению значения других вершин (и этой вершины в том числе). Контуры, противодействующие отклонению, называются контурами отрицательной обратной связи.
Устойчивость орграфов.
Вершина i орграфа называется импульсно устойчивой в импульсном процессе, если последовательность {|pi(t)|,t = 0,1,2…} ограничения, т. е. существует такое положительное число М, что{|pi(t)| меньше М для всех t.
Вершина называется устойчивой по значению в импульсном процессе, если последовательность значений вершины ограничена.
Взвешенный орграф называется импульсно устойчивым в импульсном процессе, если каждая из его вершин импульсно устойчива.
Понятие устойчивости играет важную роль в моделировании. При математической постановке задач с помощью системного подхода прежде всего учитывается, что в данной системе присутствует человек и именно он делает систему устойчивой при каждом импульсном воздействии. Если допущена ошибка (импульсное воздействие), то система становится хуже, но не распадается, поэтому при следующем импульсном воздействии негативные последствия гасятся. Конечно, последовательностью импульсных воздействий можно сделать систему неустойчивой, но из-за одного импульса этого сделать нельзя.
Для того чтобы добиться нужного поведения модели, необходимо определить круг элементов модели, на которые можно воздействовать, а именно:
· изменить на определенное время значения показателей некоторых вершин орграфа;
· изменить на определенное время знак, весовой коэффициент или функцию определенной дуги или ряда дуг;
· изменить временное запаздывание на одной или нескольких дугах;
· добавить новую дугу в орграф;
· убрать имеющуюся в орграфе дугу (для этого достаточно приравнять к нулю весовой коэффициент при этой дуге);
· создать или убрать контур;
· добавить в определенное время новую вершину и инцидентные ей (т.е. входящие) дуги;
· убрать в определенное время новую вершину и инцидентные ей дуги.
Следует помнить, что за любыми изменениями в орграфе стоит одно или несколько определенных мероприятий. Одно мероприятие может повлечь за собой комплексное изменение в орграфе, поэтому важно тщательно анализировать все производимые изменения с точки зрения их целесообразности [11,12].
Главной задачей, определяющей успех при исследовании поведения системы с помощью орграфов, считается построение модели. Прежде всего, необходимо четко и корректно определить цель исследования.
Построение орграфа состоит из следующих этапов:
1. выделение объекта исследования.
2. Определение контура, определение ее целостности.
3. Выделение факторов (вершин орграфа), определяющих поведение системы
4. Установление связей (весовые коэффициенты) между вершинами.
При этом необходимо иметь в виду, что описание самой системы возможно только при наличии описания этой системы как элемента более широкой системы. Именно такое описание системы в виде орграфа позволяет воздействовать на систему и через это воздействие проследить реакцию системы и применить методы управления этой реакцией.
Рассмотрим процесс построения орграфа на примере одного из регионов. Целью исследования будем считать определение социо-эколого-экономической перспективы развития региона.
Региональную модель представим в виде двух орграфов: первый описывает взаимодействие крупных блоков региона, второй более детализирован (рис. 3.24, 3.25).

Рис. 3.24 Схема взаимодействия основных блоков региона

Рис. 3.25 Уточненная модель взаимодействия основных блоков региона
Попробуйте проследить изменение ситуации по всем моделям на протяжении 10 шагов и сравнить полученные результаты. Отметим, что сумма значений одинаковых вершин в разных моделях различна. Эти различия следуют из принципа целостности системы.
Добавление новых вершин и связей в последующих орграфах уточняет свойства системы и более полно отражает эколого-экономическую ситуацию региона [11].
3.2.4 Показатели надёжности технических систем
Анализ безопасности и оценка риска во многом определяется надежностью технических устройств. Большинство случаев различных аварий, катастроф, взрывов, загораний, приводящих к травматизму и летальным исходам, связаны с отказами устройств, разрушениями элементов, выходами из строя агрегатов. Хотя могут быть случаи выхода из строя по вине людей, и могут быть случаи травматизма при вполне исправной работающей технике.
Надежность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования
Состояние элементов системы различают в двух позициях: работоспособное и неработоспособное.
Объект (элемент или система) считается работоспособным, если он способен выполнять свои функции и соответствует требованиям нормативно-технической документации.
Объект считается неработоспособным, если он не выполняет свои функции или по какому-то параметру не соответствует требованиям документации.
Характер перехода работоспособного объекта в неработоспособный может происходить или внезапно или постепенно. Возникновение любого вида отказа обусловлено накоплением различных изменений внутри объекта. При этом отказы, обусловленные действиями человека, не рассматриваются.
Анализ работоспособности системы с точки зрения влияния отказов отдельных элементов удобно проводить, рассматривая отдельно две системы – простые и сложные. В простых системах отказ любого элемента приводит или к отказу всей системы или вообще не влияет на качество работы всей системы. В простых системах рассматриваются два возможных состояния: работоспособное состояние, оцениваемое некоторым показателем эффективности и состояние отказа с нулевым показателем эффективности. Поэтому в простых системах надежность можно оценивать в виде безотказной работы или сохраняемости – это для невосстанавливаемых систем, а для восстанавливаемых систем – в виде ремонтопригодности и долговечности.
Сложными называются многофункциональные системы с избыточной структурой. Такие системы имеют возможность частичного или полного резервирования отдельных элементов и целых подсистем. Отказ отдельного элемента в такой системе приводит не к отказу всей системы, а только к ухудшению качества ее работы.
Надежность объекта является комплексным свойством, ее оценивают по четырем показателям — безотказности, долговечности, ремонтопригодности и сохраняемости или по сочетанию этих свойств (табл. 3.12).
Таблица 3.12 – Показатели надежности систем
| Безотказность | Свойство объекта сохранять работоспособность непрерывно в течение некоторого времени или некоторой наработки. Это свойство особенно важно для машин, отказ в работе которых связан с опасностью для жизни людей. Безотказность свойственна объекту в любом из возможных режимов его существования, в том числе, при хранении и транспортировке. |
| Долговечность | Свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. В отличие от безотказности долговечность характеризуется продолжительностью работы объекта по суммарной наработке, прерываемой периодами для восстановления его работоспособности в плановых и неплановых ремонтах и при техническом обслуживании. |
| Ремонтопригодность | Свойство объекта, заключающееся в его приспособленности к поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта. Важность ремонтопригодности технических систем определяется огромными затратами на ремонт машин. |
| Сохраняемость | Свойство объекта сохранять в заданных пределах значения параметров, характеризующих способность объекта выполнять требуемые функции, в течение и после хранения и (или) транспортирования. Практическая роль этого свойства велика для деталей, узлов и механизмов, находящихся на хранении в комплекте запасных принадлежностей. |
Безотказность. Математически вероятность безотказной работы определяется следующей математической зависимостью:
P(t)=P{T≥t}, t>0, где P(t) – вероятность безотказной работы.
Чем больше требуемое время безотказной наработки, тем меньше вероятность безотказной работы.
Долговечность – это свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.
Предельное состояние – это состояние, при котором дальнейшая эксплуатация или применение элементов по назначению недопустимо или нецелесообразно, либо восстановление невозможно или нецелесообразно.
Критерием предельного состояния служат совокупность признаков предельного состояния объекта, которые устанавливаются в нормативно-технической и конструкторской документации.
Объект может перейти в предельное состояние, оставаясь работоспособным, если его дальнейшее применение по назначению не допустимо по требованиям безопасности, экономичности или эффективности.
Для ремонтируемых объектов выделяют 3 вида предельных состояний:
средний ремонт;
капитальный ремонт;
окончательный вывод из эксплуатации.
В общем виде долговечность объектов измеряется техническим ресурсом объекта либо сроком службы, и определяется не отказом объекта, а переходом в предельное состояние, что приводит к необходимости проведения ремонта.
Одним из центральных понятий в теории надежности является понятие «наработки». Под наработкой понимается продолжительность или объем работы объекта. Наработка измеряется единицами времени или объемом выполненной работы.
Объект может работать: непрерывно (режим работы, когда объект останавливается в случаях отказа или ремонта) или с перерывами
(когда объект останавливается по причинам, которые не связаны с его техническим состоянием). Когда объект работает с перерывами, то для него вводится понятие «суммарная наработка».
Для изделий или технических систем вводят понятия:
- наработка до отказа – это наработка объекта от начала его эксплуатации до первого отказа;
- наработка между отказами – это наработка объекта после восстановления его работоспособности (отказа) до возникновения следующего отказа;
- ресурс технический – это наработка объекта от начала его эксплуатации или после ремонта до перехода его в предельное состояние;
- срок службы – это календарная продолжительность от начала эксплуатации или после ремонта определенного вида до перехода в предельное состояние.
Показатели долговечности:
средний ресурс;
назначенный ресурс;
средний срок службы;
назначенный срок службы.
Ремонтопригодность – это свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин отказов, повреждений и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта.
Свойства ремонтопригодности полностью определяется его конструкцией, т.е. свойства ремонтопригодности закладываются на этапах разработки, проектирования, изготовления и монтажа.
Кроме деления на ремонтопригодность, происходит дополнительные деления на: восстанавливаемые и невосстанавливаемые объекты. В технике существуют другие понятия: ремонтируемый и неремонтируемый объект.
Как правило, ремонтируемые объекты являются восстанавливаемыми на протяжении всего срока службы. А неремонтируемые объекты, как правило, невосстанавливаемыми. В последнее время появились элементы сложных систем, являющиеся неремонтируемыми, но самовосстанавливающимися.
Показатели ремонтопригодности:
вероятность восстановления работоспособности в заданное или за требуемое время;
среднее время восстановления;
интенсивность восстановления.
Сохраняемость – это свойство объекта сохранять показатели безотказности, долговечности, ремонтопригодности, как в течение, так и после хранения и транспортировки. Сохраняемость характеризуется способностью объекта противостоять отрицательному влиянию условий хранения и транспортировки на его безотказность и долговечность.
Срок сохраняемости – продолжительность хранения системы в определенных условиях, в течение которой сохраняются установочные показатели ее качества. Иногда сохраняемость характеризует продолжительность хранения, в течение которой техническая система сохраняет установленные показатели с заданной вероятностью гамма.
Основным показателем сохраняемости является средний срок сохраняемости.
Вероятностные характеристики отдельных свойств надежности являются независимыми. Например, объект может обладать высокими показателями безотказности, но быть плохоремонтируемым.
На практике желательно иметь объекты, обладающие высокими показателями и безотказности, и долговечности, и ремонтопригодности, но осуществить это очень трудно [3,8,9].
Контрольные вопросы:
1. Перечислите возможные источники информации для идентификации рисков процессов и систем?
2. Охарактеризуйте индивидуальные и групповые экспертные методы выявления рисков. В чем их преимущества и недостатки?
3. Дайте характеристику метода Дельфи.
4. Мозговой штурм: характеристика, достоинства, недостатки.
5. Дайте характеристику метода SWOT-анализа.
6. Дайте характеристику методов FMEA и HAZOP.
7. Перечислите основные характеристики и особенности, присущие моделям процессов и систем.
8. Что понимают под адекватностью модели? Как проверить модель на адекватность?
9. Функциональное моделирование: цели и возможности метода. Охарактеризуйте метод барьерных диаграмм.
10. Дайте характеристику метода Монте-Карло.
11. Построение моделей с помощью орграфов: характеристика и возможности метода.
12. Перечислите показатели надежности систем. Каким образом они рассчитываются?
Список использованной литературы
1. Богоявленский С.Б. Управление риском в социально-экономических системах. - СПб: Изд-во СПБГУЭФ, 2010 - 147 с.
2. Вайсман Я.И., Карманов В.В., Ерхова Н.Е. Экологический менеджмент на промышленных предприятиях: Учеб. пособие / Перм. гос. техн. ун-т. Пермь, 2006. – 127 с.
3. ГОСТ Р 51901-2002. Управление надежностью. Анализ риска технологических систем
4. Иванов А.А., Олейников С.Я., Бочаров С.А. Риск-менеджмент. Учебно-методический комплекс. – М.: Изд. центр ЕАОИ, 2008. – 193 с.
5. Кукушкина С.Н. Метод Дельфи в форсайт-проектах. Форсайт №1 (1) 2007
6. Макеева Д.Р. Оценка риска и страхование. Курс лекций http://uamconsult.com/book_425.html
7. Маюнова Н.В. Основы управления проектами. Учебный курс (учебно-методический комплекс)
8. Муравьева Е.В.,Романовский В.Л. Прикладная техносферная рискология. Экологические аспекты.- Казань, 2007.
9. МЭК 60812: 1985 Техника анализа надежности систем. Метод анализа вида и последствий отказов (FMEA).
10. «Форсайт» №1 (1) 2007
11. Холина В.Н. Основы экономики природопользования: учебник для вузов / изд-во «Питер», 2005г. – 672с.
12. Чепурных Н.В., Новоселов А.Л. Экономика и экология. Развитие, катастрофы. – М.: Наука, 1996.
13. http://www.e-college.ru/xbooks/xbook164/book/index/index.html?go=part-013*page.htm
14. http://zxshader.narod2.ru/D7/V64/.
|
|
|


