Свободные электромагнитные колебания в контуре. Превращение энергии в колебательном контуре

ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ:

(-12-9.03.2013)

Задачи по теме «Магнитный поток. Индуктивность.»

1. Найти индуктивность контура, в котором при силе тока I = 10 A возникает магнитный поток Ф = 0,5 Вб.

2. Индуктивность контура L = 0,2 Гн. При какой силе тока в нем возникает магнитный поток Ф = 0,1 Вб?

3. Индуктивность контура L = 0,04 Гн, сила тока в нем I = 0,5 А. Найти магнитный поток.

Задачи по теме «Электрические колебания»

1248. Какую роль играют индуктивность и емкость в ко­лебательном контуре?

1249. Какое влияние на свободные электромагнитные колебания в контуре окажет увеличение активного сопро­тивления катушки при прочих равных условиях?

1250. В каких случаях в колебательном контуре будут получаться незатухающие электромагнитные колебания?

1251. Для какой цели в колебательный контур иногда включают катушку переменной индуктивности или конден­сатор переменной емкости?

1252. Пластины плоского конденсатора, включенного в колебательный контур, сближают. Как будет меняться при этом частота колебаний контура?

1253. Что произойдет с собственными колебаниями в контуре, если его емкость увеличить в 3 раза, а индуктив­ность уменьшить в 3 раза? Активным сопротивлением кон­тура можно пренебречь.

1254. Вычислите частоту собственных колебаний в кон­туре, если его емкость увеличить в 3 раза, а индуктивность уменьшить в 3 раза. Активным сопротивлением контура можно пренебречь.

1255. Чему равен период собственных колебаний в кон­туре, если его индуктивность равна 2,5 мГн и емкость 1,5 мкФ?

1256. Колебательный контур содержит конденсатор электроемкостью 0,1 мкФ. Какую индуктивность надо вве­сти в контур, чтобы получить электрические колебания ча­стотой 10 кГц?

1257. Какую индуктивность надо включить в колеба­тельный контур, чтобы при электроемкости 2 мкФ получить колебания с периодом 10^-3 с?

1258. Конденсатор какой емкости надо включить в коле­бательный контур, чтобы при индуктивности катушки, рав­ной 5,1 мкГн, получить колебания с частотой 10 МГц?

1259. Плоский конденсатор состоит из двух круглых пластин диаметром 8 см. Между пластинами зажата стеклянная пластина толщиной 5 мм. Обкладки конденсатора замкнуты через катушку индуктивностью 0.02 Гн. Опреде­лите частоту колебании, возникающих в этом контуре.

1260. Колебательный контур состоит из катушки индук­тивностью 0,003 Гн и плоского конденсатора. Пластины конденсатора в виде дисков радиусом 1.2 см расположены на расстоянии 0,3 мм друг от друга. Определите период собственных колебаний контура. Каким будет период коле­баний, если конденсатор заполнить диэлектриком с диэлек­трической проницаемостью 4?

1261. Катушка индуктивностью 30 мкГн присоединена к плоскому конденсатору с площадью пластин 0.01 м и расстоянием между ними 0.1 мм. Найдите диэлектриче­скую проницаемость среды, заполняющей пространство между пластинами, если контур настроен на частоту 400 кГц.

1262. В каких пределах должна изменяться электроем­кость конденсатора в колебательном контуре, чтобы в нем могли происходить колебания с частотой от 400 до 500 Гц?Индуктивность контурной катушки равна 16 мГн.

1263. В каких пределах должна изменяться индуктив­ность катушки колебательного контура, чтобы в нем могли происходить колебания с частотой от 400 до 500 Гц? Ем­кость конденсатора равна 10 нкФ.

1264. Колебательный контур состоит из катушки индук­тивностью 4 Гн и конденсатора емкостью 1 мкФ. Амплиту­да колебаний заряда на обкладках конденсатора равна 100 мкКл. Напишите уравнение зависимости q(t), I(t), U (t).

1265. Заряд на обкладках конденсатора колебательного контура меняется по закону q = 2∙I0^-6cos (10⁴ πt) Кл. Най­дите амплитуду колебаний заряда, период и частоту коле­баний, запишите уравнение зависимости напряжения на конденсаторе от времени и силы тока в контуре от времени.

14.1. От чего зависит период собственных незатухающих электро­магнитных колебаний в контуре?

14.2. Колебательный контур состоит из конденсатора емкостью С = 1 мкФ и катушки индуктивностью L = 0,01 Гн. Вычислить период колебаний в контуре. Можно ли возникшие колебания считать высоко­частотными?

14.3. Колебательный контур состоит из лейденских банок общей элек­троемкостью С = 6∙10^-3 мкФ и катушки индуктивностью L = 11 мкГн. Вычислить частоту электромагнитных колебаний в контуре.

14.4. Катушку какой индуктивности надо включить в колебательный контур, чтобы с конденсатором емкостью С= 2 мкФ получить электро­магнитные колебания частотой v = 1000 Гц?

14.5. Какой емкости конденсатор нужно включить в колебательный контур с катушкой индуктивности L = 0,76 Гн, чтобы получить в нем электрические колебания звуковой частоты ν= 400 Гц?

14.6. Во сколько раз изменится период и частота свободных, незату­хающих колебаний в контуре, если его индуктивность увеличить в 2 ра­за, а емкость — в 4 раза?

14.7. Колебательный контур состоит из катушки индуктивностью L = 2,5∙10^-6 Гн и двух конденсаторов, соединенных между собой парал­лельно, емкостью С = 5∙10^-3 мкФ каждый. Определить период электри­ческих колебаний в контуре.

14.8. В колебательном контуре частота собственных колебаний ν₁ = 30 кГц, при замене конденсатора частота стала ν₂ = 40 кГц. Какой будет частота колебаний в контуре: а) при параллельном соединении обоих конденсаторов; б) при последовательном соединении?

Колебания и волны

Колебаниями называются такие процессы, которые обладают той или иной степенью повторяемости во времени.

Наблюдаются в системах самой разной физической природы.

Если состояние системы описывается конечным числом переменных, то мы имеем дело с собственно колебательными процессами, например, колебания груза, подвешенного на пружине, колебания маятника, колебания тока в электрическом контуре и прочие. Иными словами, в этом случае мы имеем дело с колебательными процессами, происходящими в системах, имеющих конечное число степеней свободы.

Другой тип колебательных процессов возможен в системах, имеющих бесконечное множество степеней свободы, таких, например, как сплошная среда или электромагнитное поле. В таких случаях колебательный процесс, начавшийся в одном месте, передается в соседние места, распространяясь в пространстве. Тогда говорят, что в пространстве распространяется волна. Волна характеризуется периодичностью не только во времени, но и в пространстве. Например, звук, то есть упругие волны в сплошной среде, электромагнитные волны и прочие.

Степени свободы – это число независимых переменных, позволяющих однозначно определить состояние системы в любой момент времени.

Колебательные и волновые процессы представляют собой очень важный класс процессов, важный как теоретически, так практически. Достаточно указать, что колебательные процессы используются, например, в часах (в механических и электронных), в радиоприемниках и телевизорах (колебательные контуры), акустика (звуковые волны) и прочее.

Колебания можно разделить на установившиеся и переходные. Установившиеся характеризуются периодичностью и устойчивостью. Периодичность означает, что система периодически во времени проходит один и тот же ряд состояний. Устойчивость означает, что при неизбежных в реальности случайных внешних воздействиях, она через некоторое время возвращается к установившемуся первоначальному колебанию. Переходные колебательные процессы приводят к переходу системы из данного состояния либо к состоянию устойчивого равновесия, либо к установившемуся колебательному процессу. В зависимости от характера воздействия на систему колебания разделяются на свободные и вынужденные колебания, автоколебания и параметрические колебания.

Свободными или собственными колебаниями называются такие колебания, которые происходят в системе, представленной самой себе после того как она была выведена из состояния равновесия. Например, колебания груза, подвешенного на пружине в поле тяготения.

Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается периодическому воздействию внешнего источника энергии. Например, звуковая волна, распространяющаяся в среде, где имеется источник звука или электромагнитные колебания в контуре, куда включен периодический источник энергии (ЭДС).

Автоколебания сопровождаются вводом дополнительной энергии в систему подобно вынужденным, он и в отличие от вынужденных колебаний характер ввода этой энергии определяется закономерностями самой системы, а не задается извне. Например, в механических и электронных часах.

При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы, определяющего ее внутренние свойства. Например, может периодически изменяться длина нити, на которой подвешен маятник.

Системы, в которых возможны колебательные процессы также делятся на линейные и нелинейные. Большинство физических систем нелинейны, однако, при малых отклонениях от состояний равновесия они демонстрируют линейное поведение.

Все вышеперечисленные виды колебаний реализуются в нелинейных системах, но, например, в линейных системах автоколебания не реализуются, тогда как остальные типы могут возникать.

Изучение колебательных и волновых процессов существенно облегчается тем, что между колебательными процессами различной физической природы имеет место глубокая формально-математическая аналогия. Независимо от природы системы, колебания подчиняются одинаковым по виду уравнениям, которые называются дифференциальными. Поэтому законы, по которым происходит изменение переменных, характеризующих состояние системы, со временем (и в пространстве в случае волновых процессов) оказываются для различных систем одинаковыми. Например, изменение положения груза, подвешенного на пружине, и изменение заряда конденсатора в колебательном контуре происходит по одному и тому же закону. Поэтому изучение колебаний одной физической природы значительно облегчает изучение колебаний другой природы.

Свободные электромагнитные колебания в контуре. Превращение энергии в колебательном контуре

Механические колебания представляют собой вид движения тел. На все вопросы, касающиеся таких колебаний, можно получить ответ в кинематике и динамике. Наряду с механическими колебаниями и колебательными системами существуют электрические колебания и колебательные системы. Для техники такие системы имеют еще большее значение, чем механические.

Возникает вполне закономерный вопрос: что именно и каким образом колеблется в этом случае?

Может колебаться электрический заряд на обкладках конденсатора, электрический ток в проводниках, электродвижущая сила на клеммах генератора, напряжение на каком-либо сопротивлении и т. д. Таким образом, в данном случае колеблются электрические величины. В данном случае, говоря о колебаниях электрических величин, подразумевается, что они не остаются постоянными, а меняются с течением времени. Также, подобно тому, как не всякое механическое движение является колебанием, так и не всякое изменение электрических величин со временем есть электрическое колебание.

Для механических колебаний существенной чертой является повторяемость движения, то есть его периодичность. Эта же черта является существенной и для электрических колебаний. Если изменение какой-либо электрической величины, например тока, происходит периодически, повторяясь, то можно назвать такое изменение электрическим колебанием. Примером такого процесса является всем нам известный переменный ток в осветительной электросети, который меняется по закону гармонического колебания.

Электрические колебания человек не может воспринимать непосредственно, подобно тому как он воспринимает колебания механические, например, видит колебания маятника или слышит колебания камертона. Однако, мы знаем, что и электрически заряженные тела, и проводники, по которым течет электрический ток, взаимодействуют между собой с некоторыми силами. На измерении этих сил основано измерение самих электрических величин: зарядов, токов, напряжений и т. д. Благодаря этим силам получается механическое движение в электродвигателях. С помощью этих же (электростатических и электродинамических) сил можно самыми различными способами превратить электрические колебания в механические. Например, одним из способов превращения колебаний тока в механические колебания состоит в использовании поворота катушки с током в магнитном поле. На этом основано устройство осциллографа.

 

Колебательный контур.

Переменный ток в осветительной сети получается потому, что генераторы на электростанции дают переменную электродвижущую силу. Такая электродвижущая сила возникает, например, в проволочной рамке, равномерно вращающейся в магнитном поле, причем ее период определяется угловой скорость вращения рамки. Таким образом, колебания тока в цепи вызываются колебаниями электродвижущей силы, действующей в этой цепи, подобно тому как вынужденные колебания тела вызываются колебаниями приложенной к нему механической силы. Колебания тока являются в данном случае вынужденными колебаниями.

Но существуют такие электрические цепи, в которых могут происходить свободные электрические колебания, то есть колебания без действия какой-либо внешней периодической электродвижущей силы, другими словами, существуют электрические колебательные системы. Простейшей системой такого рода является колебательный контур. Так называется цепь, которая получается при подсоединении конденсатора к катушке индуктивности (рис 49а.). Электрические свойства такой цепи определяются емкостью С конденсатора, индуктивностью L катушки и сопротивлением цепи (то есть в основном катушки) R. Для того чтобы возникли свободные колебания, надо каким-либо способом нарушить состояние равновесия – зарядить конденсатор или возбудить (индуцировать) ток, а затем предоставить контур самому себе. На рис 49,а. контур выводится из состояния равновесия тем, что конденсатору сообщается начальный заряд. Для этого служат батарея и переключатель. При одном положении переключателя (положение 1 на рис.49а) контур разомкнут и конденсатор подключен к батарее, которая и заряжает его до напряжения на клеммах батареи. Переводя переключатель в положение 2, мы отключаем батарею и замыкаем контур. С этого момента в контуре и начинаются свободные электрические колебания: заряд и напряжение на конденсаторе попеременно меняет знак, проходя через нулевое значение (на рис. 49,б показано сплошной линией). Аналогичным образом меняется ток в контуре (штриховая линия на том же рисунке), но со сдвигом по времени: ток проходит через нуль приблизительно в те моменты, когда напряжение на конденсаторе имеет наибольшие положительные и отрицательные значения.

Чем меньше сопротивление контура R, тем меньше затухание колебаний и тем точнее совпадают по времени моменты прохождения тока через нуль с моментами наибольших значений напряжения на конденсаторе. В идеальном случае полного отсутствия сопротивления колебания тока и напряжения изображались бы двумя синусоидами, сдвинутыми на четверть периода. Рассмотрим электрические колебания в идеальном, т. е. не имеющем сопротивления, колебательном контуре. В данном случае свободные незатухающие колебания называются собственными. Магнитное поле не может мгновенно появиться или исчезнуть. Всякое изменение магнитного поля сопровождается возникновением электродвижущей силы индукции, которая вызывает в проводах индукционный ток. Направление этого тока по закону Ленца таково, что создаваемое им магнитное поле стремится компенсировать изменение магнитного поля, вызывающего индукцию. Это индукционное магнитное поле замедляет изменение начального поля, препятствуя его мгновенному исчезновению или появлению. Таки образом, получается, что магнитное поле обладает инерцией подобно инерции тела. Тело не может мгновенно остановиться или сдвинуться с места, так как это означало бы, что оно приобретает бесконечно большое ускорение и, следовательно, по закону Ньютона, потребовало бы бесконечно большой силы.

Когда мы замыкаем заряженный конденсатор на катушку, то в первый момент напряжение на конденсаторе максимально, а ток в цепи равен нулю. Однако с этого момента начинается движение зарядов, перетекающих с одной обкладки на другую и, поэтому появляется ток, вызывающий магнитное поле. Магнитное поле, а значит, и обусловливающий его ток не могут мгновенно принять свое максимальное значение, а будут нарастать постепенно. Поскольку ток переносит заряды с одной обкладки на другую, напряжение на конденсаторе постепенно падает (конденсатор разряжается). Таким образом, увеличение индукции магнитного поля идет параллельно с убыванием напряженности электрического поля. Это соответствует закону сохранения энергии, так как согласно ему увеличение энергии магнитного поля должно сопровождаться уменьшением энергии электрического поля. Поэтому, когда напряжение на конденсаторе станет равным нулю и электрическая энергия исчезнет, магнитная энергия достигнет максимума. В этот момент будут максимальными и ток и индукция магнитного поля в катушке.

Так как магнитное поле (а значит, и ток) не может сразу исчезнуть, то перетекание заряда будет продолжаться в том же направлении и конденсатор начнет заряжаться, но обкладка, бывшая ранее отрицательной, будет теперь заряжаться положительно, и обратно. Ток будет ослабевать и в определенный момент обратится в нуль, конденсатор же в этот момент будет вновь заряжен до наибольшего напряжения, но с обратным знаком. Далее, ток будет течь в обратную сторону, так что в итоге конденсатор вновь перезарядится, т. е. мы вернемся к исходному состоянию, которое было в момент замыкания переключателя. На рис. 50 показаны пять состояний контура – через каждые четверть периода, последний рисунок (по истечении полного периода) совпадает с первым. Штриховыми линиями показаны линии электрического поля в конденсаторе и линии магнитного поля в катушке.

 

Простейшей электрической колебательной системой является колебательный контур. Это цепь, составленная из последовательно соединенных катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R. Если сопротивление контура R=0 то колебательный контур называют идеальным.

Свободные электромагнитные колебания в контуре – это периодические изменения заряда q и напряжения u на обкладках конденсатора и силы тока i, текущего через катушку индуктивности и резистор.

Колебания в контуре можно вызвать, сообщив обкладкам конденсатора некоторый начальный заряд или возбудив в катушке индуктивности электрический ток (например, путем включения внешнего магнитного поля, пронизывающего витки катушки). Процесс колебаний в такой цепи заключается в периодической перезарядке конденсатора под действием ЭДС самоиндукции и в протекании переменного тока.

В идеальном колебательном контуре устанавливаются незатухающие гармонические колебания, при которых величина заряда q, напряжения u и силы тока i, изменяются по следующим законам:

q = q₀∙cos(ω₀t),

u = ,

i = q` = q_m∙ω₀∙cos(ω₀t - ) = I_m∙cos(ω₀t - )

q, u, i – мгновенные значения заряда, напряжения и силы тока.

q_m, u_m = q_m/ C_, I_m = q_m∙ ω – амплитудные значения заряда, напряжения и силы тока.

ω₀ – циклическая частота свободных колебаний в контуре.

Колебания заряда и напряжения совершаются в одной и той же фазе, а колебания силы тока отстают по фазе от напряжения на конденсаторе на .

Период свободных электромагнитных колебаний определяется формулой Томсона: T₀ = 2 π

Частота свободных электромагнитных колебаний: ν₀ = =

Циклическая частота свободных электромагнитных колебаний:: ω₀ = = 2πν₀ =

При колебаниях в контуре происходит непрерывный переход энергии электрического поля конденсатора в энергию магнитного поля катушки индуктивности, и наоборот. При незатухающих колебаниях энергия, запасенная в колебательном контуре в начальный момент времени, не изменяется с течением времени и равна: W =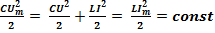

 

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: