Задания по теме «Треугольник» (повторение)

1. 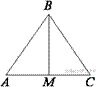В тре­уголь­ни­ке ABC AB = BC = 53, AC = 56. Най­ди­те длину ме­ди­а­ны BM.

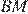2. В треугольнике известно, что , - медиана, . Найдите .

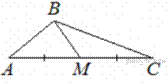
3. В треугольнике угол равен 90°, 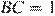, 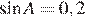. Найдите .

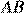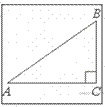
4. 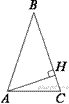В тре­уголь­ни­ке ABC AB = BC, а вы­со­та AH делит сто­ро­ну BC на от­рез­ки BH = 64 и CH = 16. Най­ди­те cos B.

5. 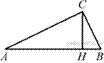В пря­мо­уголь­ном тре­уголь­ни­ке ABC катет AC = 25, а вы­со­та CH, опу­щен­ная на гипотенузу, равна 7. Най­ди­те .

6. 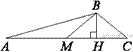В тре­уголь­ни­ке ABC BM — ме­ди­а­на и BH – высота. Известно, что AC = 216, HC = 54 и ∠ ACB = 40°. Най­ди­те угол AMB. Ответ дайте в градусах.

7. У тре­уголь­ни­ка со сто­ро­на­ми 16 и 2 про­ве­де­ны вы­со­ты к этим сто­ро­нам. Вы­со­та, про­ведённая к пер­вой сто­ро­не, равна 1. Чему равна вы­со­та, про­ведённая ко вто­рой сто­ро­не?

8. 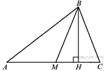В треугольнике ABC про­ве­де­ны медиана BM и высота BH. Известно, что AC = 15 и BC = BM. Най­ди­те AH.

9. У тре­уголь­ни­ка со сто­ро­на­ми 12 и 3 про­ве­де­ны вы­со­ты к этим сто­ро­нам. Вы­со­та, про­ведённая к пер­вой сто­ро­не, равна 1. Чему равна вы­со­та, про­ведённая ко вто­рой сто­ро­не?

10. Углы B и C тре­уголь­ни­ка ABC равны со­от­вет­ствен­но 62° и 88°. Най­ди­те BC, если ра­ди­ус окружности, опи­сан­ной около тре­уголь­ни­ка ABC, равен 12.

11. 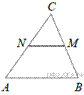В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь тре­уголь­ни­ка CNM равна 94. Най­ди­те пло­щадь четырёхугольника ABMN.

12. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна 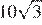, а угол между ними равен 60°. Най­ди­те площадь треугольника.

13. 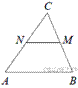В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь тре­уголь­ни­ка CNM равна 38. Най­ди­те пло­щадь четырёхугольника ABMN.

14. В треугольнике 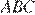отмечены середины 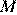и 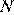сторон и 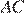соответственно. Площадь треугольника равна 24. Найдите площадь четырёхугольника .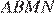

15. Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.

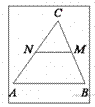
16. 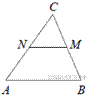В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь тре­уголь­ни­ка CNM равна 12. Най­ди­те пло­щадь четырёхугольника ABMN.

17. 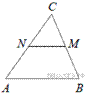В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь тре­уголь­ни­ка CNM равна 21. Най­ди­те пло­щадь четырёхугольника ABMN.

18. 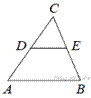В тре­уголь­ни­ке ABC известно, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 45. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

19. В тре­уголь­ни­ке одна из сто­рон равна 12, дру­гая равна 10, а ко­си­нус угла между ними равен 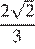. Най­ди­те площадь треугольника.

20. В тре­уголь­ни­ке ABC известно, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 7. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

21. Мальчик прошёл от дома по на­прав­ле­нию на во­сток 550 м. Затем по­вер­нул на север и прошёл 480 м. На каком рас­сто­я­нии (в метрах) от дома ока­зал­ся мальчик?

22. 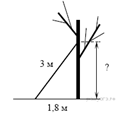Лестницу дли­ной 3 м при­сло­ни­ли к дереву. На какой вы­со­те (в метрах) на­хо­дит­ся верхний её конец, если ниж­ний конец от­сто­ит от ство­ла дерева на 1,8 м?

23. 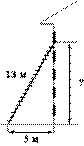По­жар­ную лест­ни­цу дли­ной 13 м при­ста­ви­ли к окну пя­то­го этажа дома. Ниж­ний конец лест­ни­цы от­сто­ит от стены на 5 м. На какой вы­со­те рас­по­ло­же­но окно? Ответ дайте в мет­рах

24. Лестница со­еди­ня­ет точки A и B и со­сто­ит из 30 ступеней. Вы­со­та каж­дой сту­пе­ни равна 16 см, а длина равна 63 см. Най­ди­те рас­сто­я­ние между точ­ка­ми A и B (в метрах).

25. 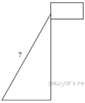Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном положении, на­хо­дит­ся на вы­со­те 4,4 м от земли. Рас­сто­я­ние от ос­но­ва­ния флагштока до места креп­ле­ния троса на земле равно 3,3 м. Най­ди­те длину троса в метрах.

26. 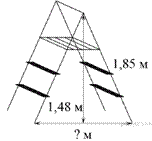Длина стре­мян­ки в сло­жен­ном виде равна 1,85 м, а её вы­со­та в раз­ло­жен­ном виде со­став­ля­ет 1,48 м. Най­ди­те рас­сто­я­ние (в метрах) между ос­но­ва­ни­я­ми стре­мян­ки в раз­ло­жен­ном виде.

27. 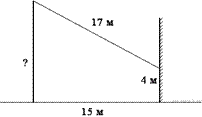От стол­ба к дому на­тя­нут про­вод дли­ной 17 м, ко­то­рый за­креплён на стене дома на вы­со­те 4 м от земли (см. ри­су­нок). Вы­чис­ли­те вы­со­ту стол­ба, если рас­сто­я­ние от дома до стол­ба равно 15 м.

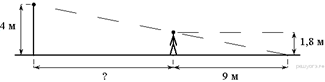
28. На каком рас­сто­я­нии (в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 1,8 м, если длина его тени равна 9 м, вы­со­та фо­на­ря 4 м?

29. Девочка про­шла от дома по на­прав­ле­нию на запад 880 м. Затем по­вер­ну­ла на север и про­шла 900 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 400 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

30. Девочка про­шла от дома по на­прав­ле­нию на запад 20 м. Затем по­вер­ну­ла на север и про­шла 800 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 200 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Прототипы задания № 24

31. Сто­ро­ны AC, AB, BC тре­уголь­ни­ка ABC равны 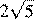, 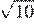и 2 со­от­вет­ствен­но. Точка K рас­по­ло­же­на вне тре­уголь­ни­ка ABC, причём от­ре­зок KC пе­ре­се­ка­ет сто­ро­ну AB в точке, от­лич­ной от B. Из­вест­но, что тре­уголь­ник с вер­ши­на­ми K, A и C по­до­бен ис­ход­но­му. Най­ди­те ко­си­нус угла AKC, если ∠ KAC >90°.

32. 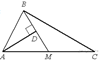Пря­мая AD, пер­пен­ди­ку­ляр­ная ме­ди­а­не ВМ тре­уголь­ни­ка АВС, делит угол ВАС по­по­лам. Най­ди­те сто­ро­ну АВ, если сто­ро­на АС равна 4.

33. Медианы тре­уголь­ни­ка 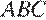пе­ре­се­ка­ют­ся в точке 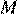. Най­ди­те длину медианы, проведённой к сто­ро­не 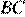, если угол 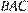равен 26°, угол 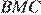равен 154°, .

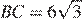34. Сто­ро­ны AC, AB, BC тре­уголь­ни­ка ABC равны 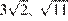и 1 со­от­вет­ствен­но. Точка K рас­по­ло­же­на вне тре­уголь­ни­ка ABC, причём от­ре­зок KC пе­ре­се­ка­ет сто­ро­ну AB в точке, от­лич­ной от B. Из­вест­но, что тре­уголь­ник с вер­ши­на­ми K, A и C по­до­бен ис­ход­но­му. Най­ди­те ко­си­нус угла AKC, если ∠ KAC >90°.

35. Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 18, DC = 54, AC = 48.

Прототипы задания № 25

36. 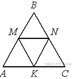В рав­но­сто­рон­нем тре­уголь­ни­ке ABC точки M, N, K — се­ре­ди­ны сто­рон АВ, ВС, СА со­от­вет­ствен­но. До­ка­жи­те, что АMNK — ромб.

37. Докажите, что бис­сек­три­сы углов при ос­но­ва­нии рав­но­бед­рен­но­го тре­уголь­ни­ка равны.

38. Два рав­но­сто­рон­них тре­уголь­ни­ка имеют общую вершину. Докажите, что от­ме­чен­ные на ри­сун­ке от­рез­к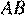и и 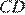равны.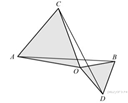

39. 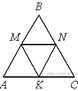В рав­но­сто­рон­нем тре­уголь­ни­ке ABC точки M, N, K — се­ре­ди­ны сто­рон АВ, ВС, СА со­от­вет­ствен­но. До­ка­жи­те, что ВMKN — ромб.

40. 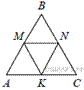В рав­но­сто­рон­нем тре­уголь­ни­ке ABC точки M, N, K — се­ре­ди­ны сто­рон АВ, ВС, СА соответственно. Докажите, что тре­уголь­ник MNK — равносторонний.

Прототипы задания № 26

41. В тре­уголь­ни­ке ABC бис­сек­три­са BE и ме­ди­а­на AD пер­пен­ди­ку­ляр­ны и имеют оди­на­ко­вую длину, рав­ную 208. Най­ди­те сто­ро­ны тре­уголь­ни­ка ABC.

42. В тра­пе­ции ABCD боковая сто­ро­на AB перпендикулярна ос­но­ва­нию BC. Окруж­ность про­хо­дит через точки C и D и ка­са­ет­ся пря­мой AB в точке E. Най­ди­те рас­сто­я­ние от точки E до пря­мой CD, если AD = 6, BC = 5.

43. 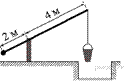На ри­сун­ке изоб­ражён ко­ло­дец с «жу­равлём». Ко­рот­кое плечо имеет длину 2 м, а длин­ное плечо — 4 м. На сколь­ко мет­ров опу­стит­ся конец длин­но­го плеча, когда конец ко­рот­ко­го под­ни­мет­ся на 0,5 м?

44. Ме­ди­а­на BM и бис­сек­три­са AP тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке K, длина сто­ро­ны AC втрое боль­ше длины сто­ро­ны AB. Най­ди­те от­но­ше­ние пло­ща­ди тре­уголь­ни­ка ABK к пло­ща­ди четырёхуголь­ни­ка KPCM.

45. В тре­уголь­ни­ке ABC на его ме­ди­а­не BM от­ме­че­на точка K так, что BK: KM = 10: 9. Прямая AK пе­ре­се­ка­ет сто­ро­ну BC в точке P. Найдите от­но­ше­ние пло­ща­ди четырёхугольника KPCM к пло­ща­ди тре­уголь­ни­ка ABС

 

Поделиться:

Воспользуйтесь поиском по сайту: