Главная | Обратная связь | Поможем написать вашу работу!

По теме «Уравнения и неравенства с двумя переменными»

Контрольная работа №1 по алгебре в 9 классе

По теме «Функции и их свойства, квадратный трехчлен»

Вариант 1

• 1. Дана функция f (х) = 17 х - 51. При каких значениях аргумента f (х) =0, f (х) < 0, f (х) > 0? Является ли эта функция возрастающей или убывающей?

• 2. Разложите на множители квадратный трехчлен: а) х ² -14 х +45; б) 3 у² +7 у- 6.

• 3. Сократите дробь .

Рис. 1

4. Область определения функции g (рис. 1) отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

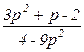5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?

Вариант 2

• 1. Дана функция g (х) = -13 х + 65. При каких значениях аргумента g (х) = 0, g (х) < 0, g (х) > 0? Является ли эта функция возрастающей или убывающей?

• 2. Разложите на множители квадратный трехчлен: а) х ²-10 х +21; б) 5 у²+ 9 у- 2.

• 3. Сократите дробь .

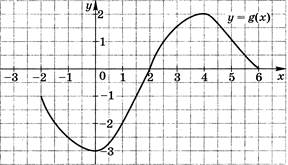
4. Область определения функции f (рис. 2) отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, класть значений функции.

Рис. 2

5. Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?

По учебнику «Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год

Контрольная работа №2 по алгебре в 9 классе

По теме «квадратичная функция и ее график»

Вариант 1

• 1. Постройте график функции у = х ² - 6 х + 5. Найдите с помощью графика:

а) значение у при х = 0,5; б) значения х, при которых у = -1;

в)нули функции; промежутки, в которых у > 0и в которых у < 0;

г) промежуток, на котором функция возрастает.

• 2. Найдите наименьшее значение функции у = х ² - 8 х + 7.

• 3. Найдите область значений функции у = х ²- 6 х - 13, где x [-2; 7].

4. Не выполняя построения, определите, пересекаются ли парабола у = 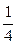х ² и прямая у = 5 х -16. Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения .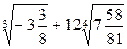

Вариант 2

• 1. Постройте график функции у = х ² - 8 х + 13. Найдите с помощью графика:

а) значение у при х = 1,5; б) значения х, при которых у = 2;

в) нули функции; промежутки, в которых у > 0 и в которых y < 0;

г) промежуток, в котором функция убывает.

• 2. Найдите наибольшее значение функции у = - х ² + 6 х – 4.

3. Найдите область значений функции у = x ² - 4 х - 7, где х [-1; 5].

4. Не выполняя построения, определите, пересекаются ли парабола у = х ²и прямая у =20-3 х. Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения .

Контрольная работа №3 по алгебре в 9 классе

По теме «Уравнения и неравенства с одной переменной»

Вариант 1

• 1. Решите уравнение: а) х ³ - 81х = 0; б) .

•2. Решите неравенство: а) 2 х ² - 13 х + 6 < 0; б) х ² > 9.

• 3. Решите неравенство методом интервалов:

а) (х + 8) (х - 4) (х - 7) > 0; б) < 0.

• 4. Решите биквадратное уравнение х ⁴ - 19 х ² + 48 = 0.

5. При каких значениях т уравнение 3 х ² + тх + 3 = 0 имеет два корня?

6. Найдите область определения функции .

7. Найдите координаты точек пересечения графиков функций у = и y = x ² - 3 x +1.

Вариант 2

• 1. Решите уравнение: а) x ³- 25 x = 0; б) .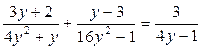

• 2. Решите неравенство: а) 2 х ² - х - 15 > 0; б) х ² < 16.

•3. Решите неравенство методом интервалов:

а) (х + 11) (х + 2) (х - 9) < 0; б) > 0.

• 4. Решите биквадратное уравнение х ⁴ - 4 х ² - 45 = 0.

5. При каких значениях п уравнение 2 х ² + пх + 8 = 0 не имеет корней?

6. Найдите область определения функции

7. Найдите координаты точек пересечения графиков функций y = и y = .
По учебнику «Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год

Контрольная работа №4 по алгебре в 9 классе

по теме «Уравнения и неравенства с двумя переменными»

Вариант 1

• 1. Решите систему уравнений: 2 x + y = 7, х ² - у = 1.	• 2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м². Найдите стороны прямоугольника.
•3. Изобразите на координатной плоскости множество решений системы неравенств: х ² + у ² 9, y x + 1.	4. Не выполняя построения, найдите координаты точек пересечения параболы у = х ²+ 4 и прямой х + у = 6.

5. Решите систему уравнений:

2 y - х = 7,

х ² – ху - у ² = 20.

Вариант 2

• 1. Решите систему уравнений x - 3 y = 2, xy + y = 6.	• 2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см².
•3. Изобразите на координатной плоскости множество решений системы неравенств: x ² +у ² 16, х + у -2.	4. Не выполняя построения, найдите координаты точек пересечения окружности х ² + у ² = 10 и прямой х + 2 у = 5.

5. Решите систему уравнений:

y - 3 x = l,

х ² - 2 ху + у ² = 9.
По учебнику «Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год

Воспользуйтесь поиском по сайту: