Оценка риска инвестиционного проекта методом сценариев

МЕТОДЫ ОЦЕНКИ РИСКА ИНВЕСТИЦИОННЫХ

ПРОЕКТОВ

Методические указания

к практическим занятиям

 

 

ПЕНЗА 2004

УДК 658.5

М

 

Рассмотрены основные методы оценки риска и учета инфляции, используемые при анализе экономической эффективности долгосрочных инвестиционных проектов. Приведены математические модели оценки риска и встроенные функции табличного процессора MS Excel, позволяющие автоматизировать инвестиционные расчеты.

 

Методические указания подготовлены на кафедре «Экономика, финансы и менеджмент» ПГУ и предназначены для студентов экономических специальностей, изучающих дисциплины «Финансовая математика» и «Экономическая оценка инвестиций».

 

Составители: И.Н. Джазовская, А.С. Похвалов

 

Под редакцией А.С. Похвалова

 

Рецензент: А.В. Понукалин, к.э.н., начальник отдела оценки бизнеса

МУП «Земинвестцентр»

 

 

ВВЕДЕНИЕ

 

Принятие инвестиционных решений всегда сопряжено с наличием некоторого риска (неопределенности) в отношении будущих результатов и условий реализации проектов. Такой риск (неопределенность) связан с большим числом случайных факторов, влияющих на ход реализации проектов, а так же возможностью лишь приближенно определить некоторые входные данные. В частности, прогноз объема сбыта, как правило, осуществляется в виде интервала, в котором с заданной вероятностью будут находится продажи продукции. Поэтому, исследование экономической эффективности инвестиционного проекта оказывается неполным без анализа степени его риска. В противном случае, оценка экономической эффективности может оказаться недостоверной.

Под риском, в общем случае, понимается вероятность отклонения фактических результатов реализации проекта от ожидаемых (прогнозируемых). При этом, чем шире диапазон возможных отклонений, тем большим считается риск. Собственно результаты оценки риска могут стать основанием для принятия решения об отклонении проекта, отсрочке момента начала его реализации или внесении изменений в условия реализации проекта. Анализ риска проекта так же может быть использован для обоснования применения конкретных методов снижения или компенсации риска.

Важным элементом оценки эффективности проекта является учет инфляционной составляющей. В условиях изменения цен возможны ситуации, при которых эффективность проекта оказывается неоднозначной при отсутствии корректировки на инфляцию. Не случайно ряд авторов относят учет инфляции к анализу риска инвестиционного проекта. Это связано не только с тем, что инфляция искажает результаты оценки, но и с тем, что методы учета инфляции могут быть легко адаптированы для анализа риска проекта.

Цель методических указаний – методическое обеспечение выполнения студентами расчетов по оценке риска инвестиционных проектов, а так же обоснование на их основе оптимальных управленческих решений. В представленных указаниях рассмотрены, получившие наибольшее распространение в практике инвестиционных расчетов, методы оценки риска и способы учета инфляции при анализе долгосрочных инвестиционных проектов. Показаны возможности автоматизации расчетов в среде табличного процессора MS Excel.

Оформление выполненной работы производится студентами в виде отчета, где отражаются цель и порядок выполнения работы, основные формулы, необходимые таблицы и графики по результатам расчетов.

 

Задача 1.

Оценка риска инвестиционного проекта методом анализа

Чувствительности

 

Цель работы – ознакомление с порядком проведения анализа чувствительности инвестиционных проектов, интерпретацией результатов такого анализа, а так же приобретение практических навыков автоматизации расчетов в среде табличного процессора MS Excel.

 

Общие сведения

Метод анализа чувствительности состоит в исследовании изменения величины некоторого показателя, характеризующего эффективность проекта, при изменении значений входящих в него параметров в заданном диапазоне. Анализ чувствительности проводится в следующей последовательности:

Шаг 1. Определение результирующего показателя и параметров инвестиционного проекта, относительно которых оценивается степень риска. В качестве результирующего, как правило, выбирается показатель финансовой эффективности проекта, например:

- величина чистой приведенной стоимости (NPV);

- индекс прибыльности (PI);

- величина изъятий (потребления) из денежного потока по периодам (Y).

В качестве параметров могут быть выбраны величины, в отношении которых имеется наибольшая неопределенность значений, или от значений которых в наибольшей степени количественно зависит результирующий показатель.

Шаг 2. Построение математической модели, отражающей количественную зависимость результирующего показателя от выбранных параметров. Например, упрощенная модель расчета величины чистой приведенной стоимости (NPV) проекта в условиях однономенклатурного производства имеет вид:

, (1)

, (2)

, (3)

где I_t – величина инвестиционных расходов по проекту в период t, руб.;

q_t – объем выпуска (реализации) продукции по проекту в период t, шт.;

p_t и c_t – цена и переменные издержки на единицу продукции в периоде t, руб.;

C_Ft и A_t – постоянные расходы (включая амортизацию) и сумма амортизации, подлежащие покрытию в периоде t, руб.;

S_n – ликвидационная стоимость имущества в момент завершения проекта t=n, руб.;

w_t – безразмерный коэффициент в периоде t;

T – ставка налога на прибыль в виде доли;

v_t – коэффициент дисконтирования в периоде t;

i_t – ставка процента в периоде t, в виде доли;

n – общее число периодов реализации проекта.

Шаг 3. Установление предельных значений результирующего показателя, при достижении которых проект считается неэффективным или высоко рискованным. В частности, при использовании в анализе чувствительности показателя чистой приведенной стоимости (NPV), в качестве предельного значения обычно выбирают NPV = 0. В целом, выбор предельных значений может быть проведен на основе VAR – анализа проекта (от англ. «value at risk» - стоимость в условиях риска).

Шаг 4. Определение интервала значений параметров проекта, входящих в оценочную модель, при которых результирующий показатель достигает установленной предельной величины. Решение представленной задачи может быть проведено двумя способами:

- используется любой прием численного решения задачи нахождения корня уравнения, отражающего равенство результирующего показателя предельной величине (метод линейной интерполяции, метод Ньютона - Рафсона). Если в качестве результирующего показателя выбран NPV, то исследуется уравнение NPV=0.

- анализ проводится путем выделения диапазона изменения выбранного параметра и шага изменения. Для каждого из возможных значений параметра рассчитывается значение результирующего показателя. Расчеты прекращаются на шаге, при котором величина результирующего показателя оказывается меньше предельной величины.

При этом, возможны две ситуации:

- исследуется влияние какого-либо одного параметра. В этом случае, значения всех параметров, кроме выбранного для анализа, фиксированы и не меняются в процессе расчета;

- исследуется одновременное влияние нескольких параметров. В этом случае, определяются диапазоны значений выбранных параметров, множество сочетаний которых обеспечивает результирующему показателю достижение предельной величины.

Шаг 5. Интерпретация полученных результатов. Метод анализа чувствительности позволяет определить устойчивость результата проекта от его входных параметров. Проект является достаточно устойчивым, если относительное отклонение параметров, при котором достигается предельная величина, составляет не менее 15 – 20% для одного параметра, и неустойчивым – если отклонение составляет менее 10%. Совместное изменение двух или более параметров, способно ослаблять или усиливать устойчивость результатов проекта.

В целом, анализ чувствительности может быть использован для установления значений отдельных плановых параметров при ненадежности исходных данных, а так же для оценки альтернативных вариантов реализации проекта, обладающих различной чувствительностью к колебаниям факторов. Недостатком метода является то, что он не содержит конкретных правил принятия решений в условиях риска.

 

Порядок выполнения работы

Провести оценку риска группы инвестиционных проектов по показателю чистой приведенной стоимости (NPV), используя метод анализа чувствительности:

1. Построить в среде табличного процессора MS Excel шаблон расчета величины чистой приведенной стоимости (NPV), соответствующий соотношениям (1) – (3).

2. По каждому из проектов определить, при каких значениях какого – либо одного параметра, величина NPV проектов равна нулю, и какова при этом величина относительного отклонения параметров от ожидаемого (базового) значения. Исходные данные по проектам и параметры, подлежащие исследованию, выдаются преподавателем.

3. Провести анализ чувствительности каждого проекта при изменении одновременно двух параметров. Построить поверхности чувствительности проектов. Параметры, подлежащие исследованию, указываются преподавателем.

4. Сделать выводы относительно степени риска каждого проекта в отдельности. Провести сравнительный анализ риска проектов в группе.

 

Пример выполнения работы

Пусть инвестиционный проект характеризуется следующими параметрами:

Периоды
It	-28000
Sn
qt
pt
ct
CFt
At
T	0,24	0,24	0,24	0,24	0,24	0,24	0,24	0,24
it		0,15	0,15	0,18	0,18	0,2	0,2	0,2

1. Создадим в среде MS Excel шаблон расчета величины NPV, где в табличной форме представлены соотношения (1) - (3) (см. рис. 1).

 

Рисунок 1 Шаблон расчета величины NPV для анализа чувствительности

 

2. При определении границ изменения параметра проекта применим встроенную функцию «Подбор параметра» из меню «Сервис», реализующую один из численных методов решения уравнений. В графе «Установить в ячейке» укажем ячейку, где ведется расчет величины NPV, а в графу «Значение» вводим ноль. Для заполнения графы «Изменяя значение ячейки» в табличную форму расчетов вводим некоторый коэффициент пропорциональности k, на который следует умножить исследуемый параметр проекта.

Например, если анализ чувствительности проводится относительно цены на изделие, то мы должны ввести в формулу расчета указанный коэффициент в виде k*p_t. Таким образом, мы предполагаем, что исследуется чувствительность всего вектора цен (параллельный сдвиг вектора цен во времени). Первоначальное значение коэффициента следует принять равным k=1.

В исходной ситуации, величина NPV = 1489,28 руб. При использовании функции «Подбор параметра» значение NPV = 3,64*10^-12» 0 руб., а значение коэффициента k = 0,98238 (см. рис. 2). Таким образом, при снижении цен на изделие более чем на 1,762 % ((1- 0,98238)*100%) в течение всего срока реализации проекта может привести к признанию проекта неэффективным.

 

Рисунок 2 Результаты анализа чувствительности проекта к изменению цены на продукцию

 

Аналогичные расчеты для других параметров проекта дали следующие результаты:

 

Параметр	Величина относительного отклонения параметра от исходного значения, при котором величина NPV=0, в %
Цена изделия	- 1,762
Переменные издержки	+3,232
Объем реализации	-3,872
Постоянные расходы	+6,055
Инвестиционные расходы	+5,319
Ставка процента	+10,447

 

3. Рассмотрим ситуацию одновременного изменения двух параметров. В этом случае, можно воспользоваться приемом, предполагающим фиксацию изменения некоторых из них и анализ чувствительности проекта к вариации какого-либо одного из них. Многократные вычисления при разных фиксированных уровнях параметров позволяют получить многомерную «поверхность» чувствительности проекта.

Проведем анализ чувствительности проекта к одновременному изменению цены p_t и объема реализации q_t. Модифицируем наш шаблон расчетов за счет введения множества коэффициентов пропорциональности k1, k2, …, k8 для всех параметров и присвоим им первоначальные значения ki=1. Пусть в качестве фиксированных изменений приняты изменения объема выпуска q_t с диапазоном 2% (k1 = 0,98; 0,96;…). Тогда, расчет чувствительности примет вид, показанный на рисунке 3.

Рисунок 3 Шаблон анализа чувствительности при изменении нескольких параметров

 

Результаты итерационных расчетов представим в следующей таблице:

 

Номер расчета (итерации)	Величина относительного отклонения объема реализации от исходного значения (фиксированный параметр), в %	Величина относительного отклонения (снижения) цены от исходного значения, при котором величина NPV=0, в %
	+4	-3,443
	+2	-2,620
		- 1,762
	-2	-0,870
	-4	Снижение цены недопустимо

 

Поверхность чувствительности проекта в этом случае примет вид:

 

4. На основе сравнения с нормативными величинами отклонений, можно заключить, что проект обладает высокой чувствительностью к своих изменению характеристик (все отклонения не превышают 10%) и окажется эффективным фактически, лишь при неизменных значениях параметров. Его риск следует признать высоким, поскольку параметры проекта в процессе плановых расчетов определяются с погрешностью, как правило, не менее 3 – 5%.

Совместное изменение факторов, как показали расчеты, приводит к росту чувствительности проекта. В случае сокращения объема продаж, допустимое снижение цены изменяется пропорционально уменьшению объема продаж и оказывается гораздо меньше, чем при исследовании снижения только цены (см. рис. 4). При этом, построение и анализ поверхности чувствительности проекта позволяет устанавливать предельные значения отдельных параметров проекта. Например, цены изделий или объема продаж по периодам.

Задача 2.

Оценка риска инвестиционного проекта методом сценариев

 

Цель работы – исследование особенностей анализа риска инвестиционных проектов на основе вероятностной информации, а так же приобретение практических навыков использования встроенных статистических функций табличного процессора MS Excel.

 

Общие сведения

Метод сценариев состоит в анализе показателей эффективности проекта на основе информации о вероятности реализации того или иного сочетания значений его параметров. Метод сценариев реализуется в следующей последовательности:

Шаг 1. Определение возможных вариантов (сценариев) изменения параметров проекта, характеризующихся наибольшей неопределенностью значений, и вероятностей их реализации. Минимальное число вариантов (сценариев), как правило, равно трем: пессимистический, оптимистический и наиболее вероятный. В отличие от метода анализа чувствительности, каждый вариант (сценарий) характеризует возможные значения одновременно всех параметров проекта, ассоциированных с данной вероятностью реализации сценария. Вероятности реализации того или иного варианта обычно определяются:

- методом субъективных вероятностей,

- методом частотного анализа,

- методом статистических испытаний,

и характеризуются дискретным или непрерывным распределением произвольного или известного вида.

Шаг 2. Оценка показателя эффективности проекта при заданных вероятностях реализации каждого варианта. Пусть в качестве показателя эффективности проекта (результата проекта) выбран критерий чистой приведенной стоимости (NPV). Тогда необходимо определить величину математического ожидания потока поступлений и платежей в каждом периоде t:

, (4)

где F_tj – величина потока поступлений и платежей по j -му сценарию в период t, руб.;

p_tj – вероятность реализации j -го сценария в период t, причем ;

m – число сценариев реализации проекта.

В этом случае, результат проекта рассчитывается в виде математического ожидания величины NPV:

, (5)

где v_t – коэффициент дисконтирования в периоде t;

n – общее число периодов реализации проекта.

Шаг 3. Оценка вероятностных характеристик показателя эффективности проекта (результата проекта). Предполагает расчет:

А. среднеквадратического отклонения (СКО) результата проекта. При определении СКО результата проекта возникает проблема корреляции между последовательными потоками поступлений и платежей. Причем, возможны три ситуации:

- потоки поступлений и платежей взаимно независимы во времени (коэффициент корреляции r = 0);

- потоки поступлений и платежей полностью взаимозависимы во времени (коэффициент корреляции r» 1);

- потоки поступлений и платежей обладают слабой зависимостью во времени (коэффициент корреляции 0 < r < 1).

Формулы расчета величины СКО результата проекта для крайних случаев r = 0 и r» 1 при нормальном характере распределения потоков поступлений и платежей имеют вид:

, (6)

, (7)

где s₀ и s₁ - СКО результата проекта соответственно для значения коэффициента корреляции потоков поступлений и платежей r = 0 и r» 1, руб.;

s_t – СКО потока поступлений и платежей от ожидаемой величины в периоде t, руб.,

. (8)

Б. коэффициента вариации результата проекта:

, (9)

где s - СКО результата проекта.

Чем ниже значение коэффициента вариации, тем меньше колеблемость результатов проекта относительно наиболее вероятного значения и, следовательно, ниже риск проекта. Риск проекта многократно возрастает при значении V > 1.

В. вероятности p(NPV < x) нахождения показателя эффективности проекта ниже заданной минимально допустимой величины x:

, (10)

где F(x) - функция распределения для величины результата проекта.

В предположении о нормальном распределении потоков поступлений и платежей, вероятность того, что величина результата проекта окажется ниже нуля находится из соотношения:

, (11)

где 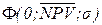– функция распределения нормальной случайной величины при данных средней величине результата проекта и его СКО - s.

Шаг 4. Интерпретация полученных результатов. Метод сценариев позволяет оценить вариацию доходов и обосновать принятие решений непосредственно на основе сравнения вероятностей неблагоприятного исхода по альтернативным проектам. Проект с меньшей вероятностью p(NPV < 0) получения убытков, является менее рискованным и, при прочих равных условиях, более предпочтительным для включения в инвестиционный портфель. Формально, предельно допустимая вероятность p(NPV < 0) не превышает 8 – 10%. Нормальной считается p(NPV < 0) £ 0,05. При этом, метод сценариев учитывает влияние на оценку риска проекта статистической зависимости между потоками поступлений и платежей. Это расширяет его предикативные возможности, по сравнению с другими методами оценки риска.

В целом, метод сценариев позволяет учесть большое число факторов, влияющих на реализацию проекта. Однако, метод сценариев не позволяет анализировать влияние отдельных параметров на результат проекта. Он так же как и метод анализа чувствительности, оказывается более информативным при сравнительном анализе различных проектов, включаемых в инвестиционный портфель предприятия.

Порядок выполнения работы

Провести оценку риска группы инвестиционных проектов по показателю чистой приведенной стоимости (NPV), используя метод сценариев:

1. Построить в среде табличного процессора MS Excel шаблон расчета величины чистой приведенной стоимости (NPV) и вероятностных характеристик проекта, соответствующий соотношениям (4) – (11) метода сценариев.

2. Используя исходные данные, выданные преподавателем, провести расчет вероятностных характеристик показателя эффективности проектов.

3. Сделать выводы относительно степени риска каждого проекта и провести сравнительный анализ риска проектов в группе.

 

Пример выполнения работы

Пусть имеется 3 сценария реализации инвестиционного проекта, характеризующихся различными вероятностями наступления:

 

Периоды
Потоки поступлений и платежей Ftj
Сценарий 1	-14000
Сценарий 2	-15000
Сценарий 3	-18000
Вероятность реализации сценария ptj
Сценарий 1	0,25	0,2	0,3	0,3	0,3
Сценарий 2	0,5	0,45	0,6	0,4	0,5
Сценарий 3	0,25	0,35	0,1	0,3	0,2
Ставка процента it	0,2	0,2	0,2	0,2	0,2

 

1. Для решения поставленной задачи воспользуемся средой ППП MS Excel и, как и ранее, создадим шаблон расчета (см. рис. 5), где в табличной форме представлены соотношения (4) - (11).

Рисунок 5 Шаблон расчетов по методу сценариев

 

При проведении расчетов использовались встроенные функции MS Excel. В частности, математическое ожидание потока поступлений и платежей в ячейке Е28 рассчитано как «СУММПРОИЗВ(E20:E22;E24:E26)», а СКО потока поступлений и платежей в ячейках Е34 – I34, как «КОРЕНЬ(Выражение)», где «Выражение» – это численное соотношение, соответствующее (8) (см. рис. 5). Для определения вероятности p(NPV < 0), в предположении о нормальном характере распределения потоков поступлений и платежей, использовалась встроенная функция

«НОРМРАСП(x, среднее значение, СКО, 1)»,

где x – исследуемое значение случайной величины (x = 0); найденное среднее значение случайной величины (), СКО – найденное среднеквадратическое отклонение (s), 1 – интегральный параметр, означающий, что функция возвращает значение кумулятивной функции распределения нормальной величины. Например, в ячейке Е42, показывающей вероятность убыточности проекта для случая независимых потоков поступлений и платежей, стоит следующее выражение – «НОРМРАСП(0;I32;E36;1)».

 

2. Результаты расчетов по исследуемому проекту методом сценариев представлены в таблице:

 

Показатель	Для случая независимых потоков поступлений и платежей (r = 0)	Для случая сильной положительной корреляции потоков поступлений и платежей (r» 1)
Математическое ожидание величины NPV	2654,82
СКО величины NPV	1749,4	3115,05
Коэффициент вариации	0,65895	1,17336
Вероятность падения величины NPV ниже нуля	0,06456	0,19704

 

3. Изучение результатов вычислений показывает, что предположение о характере взаимной зависимости (корреляции) потоков поступлений и платежей, может существенно повлиять на оценку степени риска реализации проекта. В случае сильной линейной корреляции потоков во времени, риск проекта оказывается гораздо выше, чем в случае их полной независимости. В терминах показателя вероятности убыточности проекта, риск различается в 3 раза: вероятность падения величины NPV ниже нуля составляет 6,5% против 19,7%.

Для реальных проектов, корреляция потоков поступлений и платежей во времени, как правило, соответствует неравенству 0 < r < 1. Поэтому, истинная оценка степени риска (вероятности падения величины NPV ниже нуля) находится между полученными крайними оценками.

 

Задача 3.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: