 |
Основные понятия и законы электротехники
|
|
|
|
Основные законы электрического поля
Закон Кулона
Изучение электрических явлений принято начинать с законов электрического поля. Электрическим полем называют одну из двух сторон электромагнитного поля, определяемого по механическому воздействию на неподвижные заряженные тела и частицы.
В основе теории электростатического поля лежит закон Кулона, являющийся обобщением опытных данных. Электростатическое поле любого заряда обнаруживается по силе, с которой поле этого заряда действует на другой заряд. Кулон опытным путем установил зависимость силы взаимодействия зарядов от их величины и расстояния между ними.
Закон Кулона. Два заряда q 1 и q 2, находящихся в однородной среде и отстоящих друг от друга на расстоянии r, действуют друг на друга с силой, пропорциональной произведению этих зарядов и обратно пропорциональной квадрату расстояния между ними
. (5.1)
В однородной среде сила взаимодействия будет отличаться от аналогичной силы в вакууме, что учитывается коэффициентом 
,
где e - абсолютная диэлектрическая проницаемость вещества,
e 0 - диэлектрическая проницаемость в вакууме, равная 8,85×10 -12 ф/м;
e r - относительная диэлектрическая проницаемость вещества.
Таким образом, закон Кулона запишется в виде
. (5.2)
Если число взаимодействующих зарядов более двух, то на каждый заряд со стороны других зарядов будут действовать кулоновские силы [согласно (5.2)].
Напряженность электрического поля
Если в точку М, находящуюся на расстоянии r от заряда q, внести «проб-ный» заряд q 0, то обнаружим силу F, определяющую взаимодействие этих двух зарядов. Будем считать, что во всех точках пространства, окружающего заряд q, всегда существует сила, обусловленная зарядом q, вне зависимости от наличия в рассматриваемой точке «пробного» заряда. Если величину «пробного» заряда
|
|
|
взять равной единице q 0 = 1, то возникающая при этом сила определяет величину напряженности электрического поля.
Напряженность электрического поля - основная физическая величина, характеризующая электрическое поле и пропорциональная величине механической силы, действующей на неподвижный положительный заряд, помещенный в данную точку поля, к величине этого заряда
. (5.3)
Напряженность 
электрического поля - векторная величина, равная пределу отношения силы, с которой электрическое поле действует на неподвижный точечный заряд, внесенный в рассматриваемую точку поля, к величине этого заряда при стремлении этого заряда к нулю
. (5.4)
Действие заряда осуществляется через охватывающие его сферические поверхности 
. Будем считать, что напряженность электрического поля изменяется обратно пропорционально площади этой поверхности
. (5.5)
В векторной форме напряженность электрического поля запишется в виде
. (5.6)
Электростатическое поле является потенциальным, поэтому можно записать [ см. формулы (1.59) и (1.50)]
(5.7)
. (5.8)
Условие (5.8) свидетельствует, что электростатическое поле имеет безвихревой характер.
Электрический потенциал
Как говорилось выше, электростатическое поле является потенциальным полем. При перемещении заряда q в электростатическом поле напряженностью Е на расстояние l совершается работа
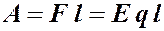. (5.9)
Потенциал поля в точке представляет собой отношение работы, совершаемой силами поля при перенесении заряда за пределы поля, к величине
заряда, когда заряд стремится к нулю
(5.10)
или
(5.11)
Так как электростатическое поле - потенциальное поле, поэтому интеграл от напряженности по любому замкнутому контуру равен нулю
|
|
|
. (5.12)
Работа, затраченная силами поля на перемещение заряда по замкнутому пути также равна нулю 
. (5.13)
Если взять две точки А и В в электростатическом поле, то линейный интеграл 
не зависит от пути интегрирования и является только функцией координат точек А и В. Величину, равную этому интегралу, называют разностью электрических потенциалов или напряжением между точками А и В и обозначают 
.
Согласно теореме Стокса [см. формулу (1.48)], для любого замкнутого контура
. (5.14)
В электростатическом поле линейный интеграл вектора 
от точки А до В не зависит от выбора пути и определяется точками А и В. Потенциал электростатического поля в точке А мы определим как линейный интеграл вектора , взятый от А до некоторой заданной точки Р, т.е. 
. Если потенциал точки Р равен 0, то
. (5.15)
Установим связь между и изменением потенциала в пространстве. Пусть О - начальная точка, а положение точки А, в которой рассматриваем потенциал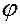 
определяется расстоянием 
вдоль пути, идущего в точку Р, где потенциал принимаем равным 0.
|
При этом можно записать, что 
, где 
- угол между 
и . Взяв производную, получим 
, откуда видно, что приращение потенциала на единицу перемещения численно равно взятой с обратным знаком составляющей в этом направлении. В частности, в декартовых координатах имеем
; 
; 
. (5.16)
Если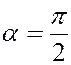 
, то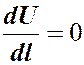 
. Следовательно, при перемещении перпендикулярно к , потенциал 
, т.е. перемещение будет происходить по поверхности равного потенциала. Линии напряженности поля нормальны к поверхностям равного потенциала. 
-уравнение этой поверхности. Следы этой поверхности в плоскости чертежа - это линии равного потенциала.
Производная от потенциала по координате имеет max в направлении нормальном к поверхности равного потенциала в сторону, противоположную . Это наибольшее значение может быть изображено в направлении против и называется градиентом электрического потенциала (grad 
). Градиент потенциала равен приращению потенциала, отнесенному к единице длины и взятому в направлении, в котором это приращение имеет максимум.
Все вышесказанное свидетельствует о том, что всякое безвихревое поле потенциальное, т.е. такое, которое может быть охарактеризовано потенциальной функцией 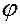=(x, y, z ).
|
|
|
И наоборот, всякое потенциальное поле является безвихревым, что вытекает из
тождества: rot grad 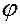= 0.
Уравнение (5.7) можно записать в форме
. (5.17)
Теорема Гаусса
Рассмотрим электрическое поле, созданное несколькими зарядами. Напря-женность такого поля определяется суммой напряженностей, создаваемых каждым зарядом в отдельности. Рассмотрим поток вектора напряженности 
через ориентированную поверхность S, который определяется согласно формуле (1.32)
. (5.18)
Теорема Гаусса. Поток вектора напряженности электрического поля сквозь замкнутую поверхность в однородном диэлектрике равен отношению электрического заряда, заключенного внутри этой поверхности, к абсолютной диэлектрической проницаемости диэлектрика
. (5.19)
Если в рассматриваемом объеме заряд отсутствует, то
. (5.20)
Вектор 
называют вектором электрического смещения. Он так же, как и вектор напряженности электрического поля, характеризует поле в каждой его точке. Соотношение
(5.21)
называют обобщенной теоремой Гаусса.
Если в рассматриваемом объеме заряд отсутствует, то
. (5.22)
Для исследования электрического поля часто пользуются теоремой Гаусса в дифференциальной форме [см. формулу (1.36) ]
или 
. (5.23)
Если вектор напряженности электрического поля представить проекциями на оси координат, то формулу (5.23) можно записать в виде
(5.24)
Учитывая (5.20), получим выражения для через потенциал
. (5.25)
Подставив в (5.22) значения 
из (5.23), получим уравнение Пуассона
. (5.26)
Интеграл 
является решением уравнения Пуассона в случае, когда заряды распределены в конечной области пространства.
Если в рассматриваемой области отсутствуют объемные электрические заряды, то уравнение Пуассона (5.26) запишется в следующем виде
. (5.27)
Таким образом, электростатическое поле удовлетворяет уравнению Лапласа.
Левые части уравнений Пуассона и Лапласа представляют собой расхождение градиентов потенциала и могут быть записаны в форме, не зависящей от системы координат
|
|
|
. (5.28)
Часто можно встретить запись уравнений (5.28) в операторной форме:
- уравнения Пуассона
или 
; (5.29)
- уравнения Лапласа
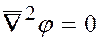или 
. (5.30)
Электрическая цепь, ее элементы и параметры
Электрический ток
Электрический ток - это явление направленного движения свободных носителей электрического заряда в веществе или вакууме.
Электрический ток проводимости в металлах и ток переноса в электровакуумных приборах представляют собой перемещение электронов, а ток проводимости в электролитах и газах - перемещение как положительных, так и отрицательно заряженных частиц (ионов). За положительное направление тока принимают перемещение положительных зарядов (это направление противоположно движению электронов). Численно ток определяется, как предел отношения количества электричества, переносимого заряженными частицами сквозь рассматриваемое поперечное сечение проводника за некоторый промежуток времени, когда последний стремится к нулю
, (5.31)
где q = q ++ q - - сумма положительных и отрицательных зарядов, переносимых в
противоположные стороны через рассматриваемое поперечное сечение провод-ника. Ток измеряется в амперах (А).
Электрический ток может быть постоянным или переменным, т.е. меняющимся в зависимости от времени.
Плотность тока
, (5.32)
где 
- плотность тока;
S - площадь сечения.
Рассматривая движущиеся заряды и их поля, различают три вида электрического тока: ток проводимости, ток переноса и ток электрического смещения.
Если заряженные частицы при движении часто встречаются с молекулами, отдавая им кинетическую энергию, то под действием постоянного усредненного поля устанавливается постоянная средняя скорость заряженных частиц. При этом в изотропной среде осредненная плотность тока может быть выражена произведением осредненной напряженности электрического поля и величины g, характеризующей электропроводность вещества и называемой удельной проводимостью вещества. Такой ток называется током проводимости (металл, полупроводники, электролиты и т.п.). Плотность тока в проводящей среде
, (5.33)
где g - удельная проводимость вещества.
Ток проводимости i ПР, представляющий собой упорядоченное движение зарядов: электронов в металле или ионов в электролите, определяется потоком вектора
плотности тока 
через поперечное сечение S проводника (5.33).
Если свободно заряженные частицы движутся в очень разряженной среде, то под действием электрического поля возникает упорядоченный ток переноса, т.к. почти нет столкновений с молекулами (например, ток переноса между электродами). Ток переноса i пер возникает в свободном пространстве, заполненном зарядами со среднеобъемной плотностью 
, движущимися со скоростью 
под действием электрического поля . Плотность тока переноса
|
|
|
, (5.34)
где - плотность заряда движущихся частиц,
- скорость их движения.
Ток электрического смещения i см возникает в диэлектриках (или вакууме) и связан с переменным электрическим полем. В частности, в электромагнитной волне электрические заряды отсутствуют и электрические токи являются замкнутыми на себя токами электрического смещения.
Плотность тока смещения в вакууме
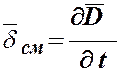. (5.35)
Токи проводимости и переноса могут возникать как в постоянных, так и переменных электрических полях, а ток смещения присутствует только в переменных полях. Таким образом, плотность полного электрического тока 
определяют суммой его составляющих
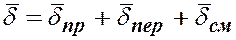(5.36)
или, учитывая значения плотностей токов,
. (5.37)
Первая и третья составляющие не могут быть вместе в одной точке пространства. Первая и вторая составляющие могут быть вместе в полупроводниках. В хорошем проводнике можно пренебречь вторым слагаемым по сравнению с первым. В диэлектрике можно пренебречь первым слагаемым по сравнению со вторым.
Результирующий ток через поверхность S
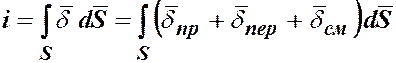. (5.38)
Очевидно, что полный электрический ток представляет собой два разнородных явления: движение электрических зарядов и изменение электрического поля во
времени. Причем токи смещения преобладают в диэлектриках, токи проводимости - в проводниках, а в полупроводниках необходимо учитывать все составляющие полного тока.
Принцип непрерывности электрического тока: Сумма токов всех родов - проводимости, переноса и смещения - сквозь любую замкнутую поверхность равна нулю
, (5.39)
где 
- плотность полного тока.
Электрическая цепь
Электрической цепью называют совокупность устройств и объектов, образующих пути для протекания электрического тока.
Элемент электрической цепи - отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию.
Различают активные и пассивные элементы электрических цепей.
Активные элементы - источники электрической энергии, преобразующие в
электрическую другие виды энергии (механическую, химическую и др.).
Пассивные элементы - элементы электрической цепи, преобразующие электрическую энергию в другие виды энергии.
Все элементы электрических цепей разделяют на две группы: линейные и нелинейные.
Линейными называются те элементы, параметры которых не зависят от про-
текающего через них тока. Если такая зависимость имеется, то элемент будет нелинейным.
Электрической схемой называется графическое изображение электрической цепи.
Ветвь - один или несколько последовательно соединенных элементов электрической цепи, через которые протекает один и тот же ток.
Узел - место соединения трех и более ветвей.
Любой замкнутый путь по нескольким ветвям называется контуром.
Напряжение
На рис. 5.2 изображен участок электрической цепи. Разность электрических потенциалов точек 1 и 2 (
и 
- потенциалы этих точек) представляет на-
пряжение на данном участке цепи
. (5.40)
|
Разность электрических потенциалов (напряжение) - величина скалярная, которая определяется работой, затраченной на перенос единичного положительного заряда из точки 1 в точку 2. Напряжение измеряется в вольтах (В). Электрическое напряжение может быть как постоянным, так и переменным, т.е. его величина может меняться во времени.
Мощность и энергия
Через участок цепи (рис.5.2) под воздействием напряжения u проходит
электрический заряд dq. Совершаемая при этом работа
, (5.41)
а мощность этой электрической цепи
. (5.42)
Мощность Р величина скалярная и может быть положительной (при совпадающих по направлению u и i) или отрицательной (если направления u и i
противоположны). В первом случае (P >0) энергия поступает в приемник, во втором (P <0) энергия возвращается из рассматриваемого участка к источнику. Мощность измеряется в ваттах (Bт).
Энергия, поступившая в приемник за время от t 1 до t 2, определяется как
. (5.43)
Она может быть только положительной и измеряется в джоулях (Дж).
Резистор. Сопротивление электрическое
Резистором называется элемент электрической цепи, в котором происходит необратимое преобразование электрической энергии в тепловую.
Условное изображение резистора приведено на рис. 5.3. Обозначение r применяют в электротехнике как для обозначения элемента цепи, так и для количественной оценки сопротивления, равного отношению напряжения на данном элементе, к току, проходящему через него
. (5.44)
Эта формула определяет закон Ома, установленный в 1826г. Величина сопротивления измеряется в омах (Ом).
Величину обратную сопротивлению
(5.45)
называют проводимостью.
Мощность резистора
. (5.46)
Величину сопротивления можно определить как отношения мощности к квадрату тока, проходящего через это сопротивление
. (5.47)
Электрическая энергия, поступающая в резистор r за время t и превращающаяся в тепло, равна
. (5.48)
Емкость. Конденсатор
Конденсатор - элемент электрической цепи, в котором накапливается энергия электрического поля. Конденсатор характеризуется емкостью
. (5.49)
Емкость измеряется в фарадах (Ф), причем емкость всегда больше нуля.
Так как ток - производная заряда во времени, то
. (5.50)
Отсюда
. (5.51)
Проинтегрировав выражение (5.51), получаем
. (5.52)
Определив константу интегрирования 
, получим
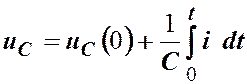, (5.53)
где 
- начальное напряжение на конденсаторе.
Мощность, потребляемая емкостью, равна
. (5.54)
Когда заряд положителен и возрастает, то ток положителен, и в емкость поступает электрическая энергия извне. Когда заряд положителен, но убывает, т.е. ток отрицателен, то энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь.
Энергия электрического поля в произвольный момент времени t (при условии, что при t=0 емкость не была заряжена) определится выражением
. (5.55)
Магнитное поле
Основные понятия и определения
Магнитным полем называют одну из двух составляющих электромагнитного поля, характеризующуюся воздействием на движущуюся электрически заряженную частицу с силой, пропорциональной заряду частицы и её скорости. Магнитное поле в любой точке характеризуется вектором магнитной индукции - 
.
Магнитная индукция определяется или по величине механической силы, с которой магнитное поле действует на движущиеся в нем заряды (электрический ток), или по ЭДС, наводимой в проводнике, движущемся в магнитном поле.
Вектор магнитной индукции определяет силу, действующую на движущийся в магнитном поле электрический заряд, и направлен по касательной к магнитной линии, проходящей через точку, в которой определяется вектор магнитной индукции
|
Поток вектора магнитной индукции сквозь некоторую поверхность S называют магнитным потоком. Магнитный поток Ф - скалярная вели-
чина, характеризующая какую-либо область магнитного поля (рис. 5.4)
, (5.56)
где d S - вектор элементарной площадки поверхности S, направленный перпендику-лярно площадке, которая пронизывается вектором 
; 
- скалярное произведение векторов и 
.
Напряженность магнитного поля 
- вектор, который характеризует магнитное поле в каждой его точке.
В вакууме напряженность поля в какой-либо точке связана с магнитной индукцией в той же точке соотношением
, (5.57)
где 
- магнитная проницаемость вакуума.
Как и любое векторное поле, поле может быть представлено наглядно с
помощью линий вектора . Их проводят обычным способом так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора , а густота линий была бы пропорциональна модулю вектора в данном месте.
Полученная таким образом геометрическая картина позволяет легко судить о конфигурации данного магнитного поля и облегчает анализ.
Теорема Гаусса для магнитного поля
Теорема Гаусса. Поток вектора сквозь любую замкнутую поверхность равен нулю
. (5.58)
Эта теорема является обобщением опыта. Она выражает собой в постулативной форме тот экспериментальный факт, что линии вектора не имеют ни начала, ни конца. Поэтому число линий вектора , выходящих из любого объема, ограниченного замкнутой поверхностью S, всегда равно числу линий, входящих в этот объем.
Отсюда вытекает важное следствие - поток вектора сквозь поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы
поверхности S. Закон выражает тот факт, что магнитное поле не имеет источников в противоположность полю электрическому.
Принцип суперпозиции
Опыт показывает, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности
. (5.59)
Закон Био - Савара
Рассмотрим вопрос о нахождении вектора магнитной индукции, создаваемой постоянными электрическими токами. Этот вопрос будем решать, исходя из равномерно движущегося точечного заряда.
Поставим в уравнение магнитного поля равномерно движущегося заряда 
, где 
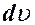- элементарный объем, - объемная плотность заряда. Кроме того,
. Тогда формула приобретет следующий вид:
. (5.60)
Если же ток I течет по тонкому проводу с площадью поперечного сечения 
, то
, (5.61)
где 
- элемент длины провода.
Введя вектор в направлении тока i, перепишем предыдущее равенство
так:
. (5.62)
Векторы 
и 
называют соответственно объемным и линейным элементами тока.
Произведя в формуле (5.60) замену объемного элемента тока на линейный, получим закон Био - Савара:
. (5.63)
Полное поле 
в соответствии с принципом суперпозиции определяется
. (5.64)
Расчет по этим формулам индукции магнитного поля тока произвольной конфигурации, вообще говоря, сложен. Однако расчет упрощается, если распре-
деление тока имеет определенную асимметрию.
Магнитное поле равномерно движущегося заряда
Опыт показывает, что само магнитное поле порождается движущимися зарядами (токами). В результате обобщения экспериментальных данных был получен элементарный закон, определяющий поле точечного заряда q, движущегося со скоростью
, (5.65)
где - магнитная постоянная; коэффициент 
;
- радиус-вектор, проведенный от заряда q к точке наблюдения.
Конец радиус-вектора 
неподвижен в данной системе отсчета, а его начало движется со скоростью 
, поэтому вектор в данной системе отсчета зависит не только от положения точки наблюдения, но и от времени.
 постоянной скоростью .
|
В соответствии с формулой (5.65), вектор (рис 5.5) направлен перпендикулярно плоскости, в которой расположены векторы и , причем вращение вокруг вектора в направлении вектора образует с направлением правовинтовую систему. Отметим, что вектор является аксиальным (псевдовектором). Магнитная индукция измеряется в теслах (Тл).
Теорема о циркуляции вектора магнитной индукции - (для магнитного поля постоянных токов в вакууме)
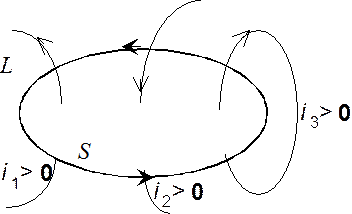
Теорема. Циркуляция вектора по произвольному контуру 
равна произведению на алгебраическую сумму токов, охватываемых контуром 
(5.66)
где 
.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Теорема о циркуляции может быть доказана, исходя из закона Био-Савара. Поскольку
доказательство громоздкое, то будем считать, что это постулат, подтвержденный экспериментально.
|
Если ток i распределен по объему, где расположен контур, то его можно представить как
. (5.67)
Интеграл берется по поверхности S, охватываемой контуром 
.
Рис. 5.6 На рис.5.6 изображена правовинтовая система. Тогда уравнение примет вид
. (5.68)
Тот факт, что циркуляция вектора , вообще говоря не равна нулю, означает, что поле не потенциально (в отличие от электростатического поля). Такое поле
 
Рис.5.7
|
называют вихревым или соленоидальным. Так как циркуляция вектора пропорциональна току i, охватываемому контуром, то магнитному полю, в общем случае, нельзя приписать скалярный потенциал, который был бы связан с вектором
|
соотношением, аналогичным .
Этот же потенциал был бы неоднозначен: при каждом обходе по контуру и
возвращении в исходную точку он получал бы приращение, равное 
.В той области пространства, где токов нет, вводят магнитный потенциал 
и достаточно эффективно используют.
Эта теорема играет примерно ту же роль, что и теорема Гаусса для векторов и 
. Поле определяется всеми токами, а циркуляция же вектора только теми токами, которые охватывают данный контур. Несмотря на это, в некоторых случаях - при наличии специальной симметрии - теорема о циркуляции оказывается весьма эффективной и позволяет очень просто находить .
Это бывает в тех случаях, когда вычисление циркуляции вектора можно свести, выбрав контур к произведению B (или 
) на длину контура или его часть.
Если этого нет, то расчет поля приходится проводить с помощью закона Био-Савара или путем решения соответствующих дифференциальных уравнений.
Электромагнитная индукция
Согласно явлению электромагнитной индукции, открытого Фарадеем в 1831г., всякое изменение магнитного поля сопровождается возникновением электрического поля. Возникающее элект
|
|
|
