Задачи для самостоятельного решения

Практическая работа № 2 (4 часа)

 

Тема: Выделение компонент сильной связности

Цель работы: Формирование умения находить матрицы сильной связности, выделять компоненты сильной связности заданного орграфа.

Материально-техническое оснащение:

Руководство к практической работе.

 

Теория

Подграфом графа G (ориентированного графа D) называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G (D).

Подграф называется собственным, если он отличен от самого графа.

Говорят, что вершина w ориентированного графа D (графа G) достижима из вершины v, если либо w=v, либо существует путь (маршрут) из v в w.

Граф (ориентированный граф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v и w.

Компонентой связности графа G (сильной связности ориентированного графа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (ориентированного графа D).

Матрицы достижимости и связности

Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где V={v₁,…, v_n}. Обозначим через A^k=[a^(k)_ij] k-ю степень матрицы смежности A(D).

Элемент a^(k)_ij матрицы A^k ориентированного псевдографа D=(V,X) (псевдографа G=(V,X)) равен числу всех путей (маршрутов) длины k из v_i в v_j.

Матрица достижимости ориентированного графа D − квадратная матрица T(D)=[t_ij] порядка n, элементы которой равны

Матрица сильной связности ориентированного графа D − квадратная матрица S(D)=[s_ij] порядка n, элементы которой равны

Матрица связности графа G − квадратная матрица S(G)=[s_ij] порядка n, элементы которой равны

Утверждение 1. Пусть G=(V,X) – граф, V={v₁,…, v_n}, A(G) – его матрица смежности. Тогда

S(G)=sign[E+A+A²+A³+… A^n-1] (E- единичная матрица порядка n).

Утверждение 2. Пусть D=(V,X) – ориентированный граф, V={v₁,…, v_n}, A(D) – его матрица смежности. Тогда

1) T(D)=sign[E+A+A²+A³+… A^n-1],

2) S(D)=T(D)&T^T(D) (T^T-транспонированная матрица, &- поэлементное умножение).

 

Алгоритм выделения компонент сильной связности

1. Присваиваем p=1 (p − количество компонент связности),

2. Включаем в множество вершин V_p компоненты сильной связности D_p вершины, соответствующие единицам первой строки матрицы S_p. В качестве матрицы A(D_p) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V_p.

3. Вычеркиваем из S_p строки и столбцы, соответствующие вершинам из V_p. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как S_p+1, присваиваем p=p+1 и переходим к п. 2.

Пример

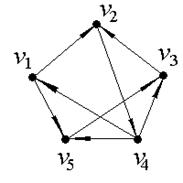
Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин n=5.

Рис. 6.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

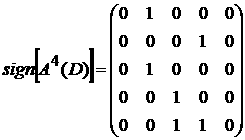
Следовательно,

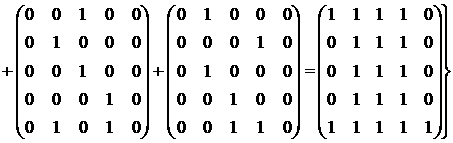
Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

Присваиваем p=1 и составляем множество вершин первой компоненты сильной связности D₁: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины

Вычеркиваем из матрицы S₁(D) строку и столбец, соответствующие вершине v₁, чтобы получить матрицу S₂(D):

Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S₂(D), то есть исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V₂:

Вычеркиваем из матрицы S₂(D) строки и столбцы, соответствующие вершинам из V₂,чтобы получить матрицу S₃(D), которая состоит из одного элемента:

и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

D1:

D2:

D3:

Задачи для самостоятельного решения

 

1. Орграф задан матрицей смежности. Определить матрицу сильной связности S(D). Используя алгоритм найти количество компонент сильной связности орграфа D и определить матрицы смежности этих компонент. Построить изображение орграфа и его компонент сильной связности.

 

а) 0 1 0 0 1 0 б) 0 1 0 0 0

0 0 0 0 0 1 1 0 0 0 0

0 1 0 1 0 0 A(D)= 0 1 0 1 0

A(D)= 0 0 1 0 0 1 0 0 0 0 1

1 0 0 1 0 1 0 0 1 0 0

0 1 0 0 0 0

 

 

2.Форма отчета

1.Разобрать решенные задачи и записать в тетрадь

2. Выполнить задачи для самостоятельного решения и оценить свою работу по следующей схеме:

1 задача – 3 балла

2 задачи - 5 баллов

 

Задание на внеаудиторную самостоятельную работу

1. С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

а) б) в)

 

 

2. Ответить на контрольные вопросы

 

Контрольные вопросы.

1. Подграф

2. Собственный подграф

3. Компонента связности, сильной связности

4. Матрица достижимости орграфа

5. Матрица сильной связности орграфа

6. Матрица связности графа

7. Нахождение матрицы связности, сильной связности

 

 

Литература

1. В.Н. Нефедов «Курс дискретной математики»

г. Москва, изд. МАИ, 2010 год

2. В. Новиков «Курс дискретной математики для программистов»

г. Москва, 2012 год

3.М.С. Спирина, П.А. Спирин «Дискретная математика»- М.: Издательский центр «Академия», 2008 год

 

Поделиться:

Воспользуйтесь поиском по сайту: