Указания к выполнению работы

Общие указания

 

Целью кинематического расчёта является определение перемещений,

скоростей и ускорений звеньев при их заданных размерах и движении ведущего

звена. Расчёт может быть осуществлён аналитически, графо-аналитическим

или графическим методом. Последние методы менее точны, чем аналитические, но проще и менее трудоёмки, благодаря чему часто применяются на практике,

когда обеспечивают требуемую точность.

В данных указаниях рассматривается графоаналитический метод определения скоростей и ускорений, а именно метод планов.

Он используется для кинематического анализа двух наиболее

распространенных схем рычажных кулисных механизмов, которые образованы

путём последовательного присоединения к начальному механизму (кривошип и

стойка) двух двухзвенных структурных групп [I].

План скоростей и его свойства

 

Планом скоростей называется графическое построение, при помощи которого определяются линейные скорости точек какого-либо звена механизма.

Рассмотрим построение плана скоростей и его свойства для звена механизма, которое совершает сложное плоское движение (рис. 1).

Пусть известна скорость точки А звена и его угловая скорость .

Определим скорости точек В и С. Согласно теореме сложения скоростей [1]

имеем:

(1)

 

Здесь и - скорости относительного вращательного движения точек В и С вокруг точки А. Они определяются из зависимостей

Отложим в произвольном масштабе на чертеже из какой-либо точки р,

называемой полюсом, отрезок, изображающий вектор скорости (рис.2).

Путем графического сложения векторов согласно (1) определяем скорости

точек В и С. Фигура, образованная при этом на рисунке, представляет собой

план скоростей для данного звена. Нетрудно доказать, что треугольник abc на

плане скоростей подобен треугольнику АВС на схеме механизма (рис.1). Эти

треугольники являются также и сходственно расположенными. В данном

случае под этим понимается расположение подобных фигур, при котором

обход их контуров в одном и том же направлении дает одинаковую

последовательность букв, расставленных в вершинах.

 

 

Рис. 4

Обход контура треугольника АВС на схеме механизма в направлении часовой стрелки дает последовательность АВСА; ту же последовательность букв дает обход по часовой стрелке треугольника abc на плане скоростей.

Способность плана скоростей образовывать фигуры, подобные и сходственно расположенные фигурам на звене механизма - это первое, наиболее важное изображающее свойство плана скоростей. Следует заметить, что фигура на плане скоростей повернута на 90° в направлении угловой скорости звена 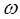по отношению к подобной фигуре на звене механизма .

Второе изображающее свойство плана скоростей состоит в том, что отрезки, выходящие из полюса, изображают абсолютные скорости точек звена механизма. Отрезки, соединяющие концы векторов абсолютных скоростей, изображают относительные скорости, направленные всегда к той букве плана скоростей, которая стоит первой в обозначении скорости. Например, скорость направлена от точки а к точке b; скорости и - от точки а и b к точке с. Изображающие свойства плана скоростей дают возможность определить скорость любой точки звена, если известны скорости двух любых его точек. Пусть, например, известны скорости точек А и В звена. Чтобы найти скорость третьей точки С, достаточно на концах векторов и плана скоростей построить треугольник аbс, подобный и сходственно расположенный с треугольником АВС на звене механизма. Проведя прямую из полюса р в точку с, получим искомый вектор .

План ускорений и его свойства

Планом ускорений называется графическое построение, с помощью которого можно определить ускорение любой точки какого-либо звена механизма.

Рассмотрим построение плана ускорений и его свойства на примере звена механизма, которое совершает сложное плоское движение (Рис. 5).

Пусть известно ускорение точки А звена, его угловая скорость и угловое ускорение .

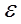Используя теорему сложения ускорений при плоском движении [I], можно получить следующие выражения для определения ускорений точек В и С;

Здесь и - центростремительные составляющие ускорения относительного вращательного движения точек В и С вокруг точки А. Они направлены всегда к центру вращения и определяются из зависимостей:

(3)

Вращательные составляющие относительных ускорений и перпендикулярны центростремительным. Их направление определяется в соответствии с угловым ускорением звена, а величина подсчитывается по формулам:

(4)

Построение плана ускорений (Рис. 6) производится аналогично построению плана скоростей путем графического сложения векторов согласно уравнениям (2).

Построив план ускорений, можно убедиться, что концы векторов ; ; образуют на плане ускорений треугольник аbс, подобный и сходственно расположенный с треугольником АВС звена механизма (Рис. 5).

Действительно,

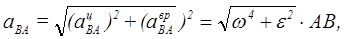(5)

(6)

Поделив выражение (5) на (6), устанавливаем, что отрезки и на плане ускорений пропорциональны отрезкам АВ и АС звена механизма.

Далее известно, что

т.е. величина угла одинакова для всех точек звена. Угол между векторами и равен углу между АВ и А С (Рис. 5).

Следовательно, угол между векторами и тоже равен , так как эти вектора наклонены по отношению к своим центростремительным составляющим в одну сторону на один и тот же угол . Таким образом, треугольник abc на плане ускорений подобен треугольнику АВС звена механизма.

Отсюда может быть отмечено главное свойство плана ускорений (аналогично плану скоростей) - способность образовывать фигуры, подобные и сходственно расположенные с фигурами на звене механизма. При этом фигура на плане ускорений повернута на угол по отношению к подобной фигуре звена механизма в направлении углового ускорения звена. Все остальные свойства плана ускорений также аналогичны соответствующим свойствам плана скоростей. Они дают возможность определить ускорения любой точки звена, если известны ускорения двух любых его точек. Построение выполняется аналогично соответствующим построениям на плане скоростей.

План скоростей и ускорений для шестизвенного

Рычажного механизма

 

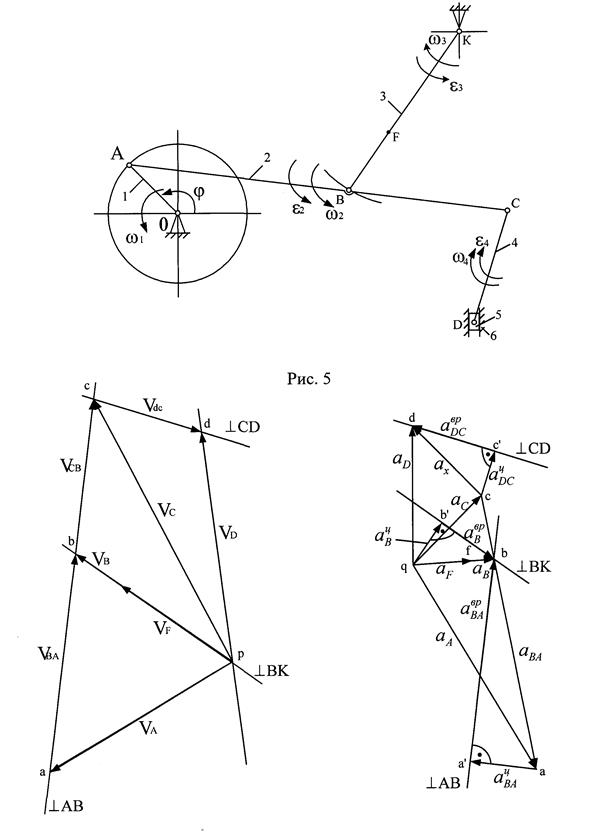
Схема механизма показана на Рис. 7. Он образован присоединением к

начальному механизму (кривошип 1 и стойка 6) двух двухзвенных структурных

групп: шатун 2 - коромысло 3 и шатун 4 - ползун 5.

Ведущее звено - кривошип 1, ведомое - ползун 5, движущийся поступательно. Размеры звеньев считаем известными. Положение механизма определяется углом поворота кривошипа. Задана величина и направление угловой скорости кривошипа. Для упрощения задачи считаем её постоянной.

Скорость точки А, принадлежащей звеньям 1 и 2, определим как окружную во вращательном движении

Вектор направлен перпендикулярно OA в сторону, соответствующую

Для определения скорости точки В, принадлежащей 2 и 3 звеньям, разложим движение звена 2 на поступательное вместе с точкой А и относительное вращательное вокруг точки А. В соответствии с этим запишем для точки В векторное уравнение

(7)

В данном уравнении вектор является известным по величине и

направлению.

Линия действия скорости относительного вращательного движения точки В вокруг точки А перпендикулярна линии АВ шатуна. Линия действия скорости перпендикулярна линии ВК коромысла, совершающему вращательное движение вокруг точки К.

Решение векторного уравнения (7) производим графически путём построения плана скоростей (Рис. 6).

Из полюса р проводим отрезок ра произвольной длины, изображающий вектор . Масштаб плана скоростей

Далее из полюса р проводим линию действия перпендикулярно линии

коромысла ВК. Из точки а конца вектора проводим линию действия перпендикулярно АВ. Точка b пересечения этих линий определяет величины скоростей

Направление векторов 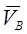и должно соответствовать уравнению (7).

Угловая скорость шатуна АВ

Схема механизма

 

 

Её направление соответствует направлению вектора

Угловая скорость коромысла ВК

Её направление соответствует направлению вектора

Для нахождения вектора скорости точки С шатуна воспользуемся

изображающими свойствами плана скоростей. В соответствии с ними три точки

одного звена на схеме механизма образуют треугольник, подобный и

сходственно расположенный с треугольником на плане скоростей, вершинами

которого являются концы векторов скоростей этих точек. В данном случае все

три точки А, В, С лежат на одной линии. Следовательно, изображающая точка

с на плане скоростей должна находиться на продолжении линии аb (за точкой

b). Её положение найдём из пропорции

Величина скорости

Аналогично можно определить скорости точки Р коромысла ВК. При этом

следует учесть, что скорость коромысла 3 известна также в двух точках: в точке

В и в точке К Изображающая точка k на плане скоростей совпадает с

полюсом р. Изображающая точка f находится на отрезке bр. Отрезок fp

найдётся из пропорции

Величина скорости . Для определения скорости точки D,

принадлежащей 4 и 5 звеньям, раскладываем движение звена 4 на переносное с

точкой С и относительное вращательное вокруг точки С. В соответствии с этим

запишем для точки D векторное уравнение

(8)

Линия действия скорости относительного вращательного движения

точки D вокруг точки С перпендикулярна линии DС шатуна. Линия действия

скоростей направлена вдоль хода ползуна. Для графического решения

уравнения (8) из полюса р проводим линию действия скорости параллельно

линии хода ползуна, а через точку с - линию действия скорости

перпендикулярно DС. Точка d пересечения этих линий определяет величины

скоростей.

Направление векторов и должно соответствовать уравнению (8).

Угловая скорость шатуна СD

Её направление соответствует направлению V ос.

Построение плана ускорений выполним для того же положения механизма

(Рис. 7). Ускорение точки А складывается из двух составляющих:

центростремительного и вращательного

Так как угловое ускорение кривошипа Следовательно,

. Вектор направлен параллельно ОА к центру вращения (точке О).

Определение ускорения точки В шатуна производится на основании

разложения движения звена 2, принятого ранее при построении плана

скоростей.

В соответствии с этим запишем для точки В векторные уравнения

(9)

При этом необходимо учесть, что ускорение точки В относительно

точки а складывается из центростремительной и вращательной

составляющих. Рассматривая точку В, как принадлежащую коромыслу ВК,

раскладываем её ускорение на центростремительное и вращательное .

Тогда уравнение (9) приобретает вид

(10)

Решение данного уравнения производим графическим путём построения

плана ускорений (рис.7).

Из полюса q проводим отрезок qa произвольной длины, изображающий

вектор . Масштаб плана ускорений

Из точки а проводим вектор параллельно АВ в направлении от точки

В к точке А.

Величина этого ускорения

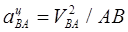
Длина соответствующего отрезка на плане ускорений

Из полюса q проводим вектор параллельно ВК в направлении от точки

В к точке К.

Величина этого ускорения

Длина соответствующего отрезка на плане ускорений

Из точки проводим линию действия вектора перпендикулярно АВ,

а из точки проводим линию действия вектора перпендикулярно ВК.

Точка b пересечения этих линий определяет величины ускорений.

Направление векторов должно соответствовать уравнениям (14), (15).

Угловое ускорение шатуна АВ:

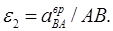
Его направление соответствует направлению вектора

Угловое ускорение коромысла ВК:

Его направление соответствует направлению вектора

Для нахождения вектора ускорения точки C воспользуемся

изображающими свойствами плана ускорений, которые аналогичны свойствам

плана скоростей. Изображающая точка c на плане будет находиться на

продолжении отрезка ab за точкой b. Величина отрезка ас определяется из

пропорции: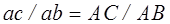

Величина ускорения Аналогично можно определить

ускорение точки F коромысла ВК. При этом следует учесть, что ускорение

коромысла 3 известно также в двух точках: в точке В и в точке К .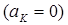

Изображающая точка k на плане ускорений совпадает с полюсом q.

Изображающая f будет находиться на отрезке bq. Отрезок fq находится из

пропорции:

Величина ускорения .

Для определения ускорения D, принадлежащей 4 и 5-му звеньям,

раскладываем движения звена 4 на переносное с точкой С, ускорение которой

уже известно, и относительное вращательное вокруг точки С. В соответствии с

этим запишем для точки D векторное уравнение

(16)

При этом учитываем, что ускорение точки D относительно точки С

складывается из центростремительного и вращательного

Тогда уравнение (11) принимает вид

(12)

Решение данного уравнения производим графически на плане ускорений.

Из конца вектора (точка с) проводим вектор параллельно DC в

направлении от точки D к С. Величина этого ускорения

Длина соответствующего отрезка на плане ускорений

Из полюса q проводим линию действия ускорения точки D, параллельно

линии хода ползуна, а из точки линию действия вектора

перпендикулярно DC. Тогда точка d пересечения этих линий определяет

величину ускорений

Направления векторов должно соответствовать уравнениям (11), (12).

Угловое ускорение шатуна CD

Его направление соответствует направлению вектора

 

Указания к выполнению работы

В бланке задания приводится кинематическая схема механизма, указаны

его размеры. Положение звеньев определяется величиной угла поворота

кривошипа. Выполнение работы производится на листах формата А4, в

соответствии с требованиями ECKD, изложенными в работе [З].

Оформленная работа должна содержать:

а) титульный лист;

b) таблица исходных данных;

с) кинематическая схема механизма, вычерченная в стандартном масштабе

с помощью чертёжных принадлежностей;

d) все необходимые векторные уравнения, пояснения к ним, расчётные

формулы, цифровые подстановки и результаты (с указаниями размерностей

физических величин).

При оформлении работы допускается применение компьютерной графики.

 

Рекомендуемая литература

1. Фролов К.В. Теория механизмов и машин. - М.: Высш. шк., 1987.

2. Иосилевич Г.Б. Прикладная механика. -М.: Высшая шк., 1989.

3. Метод, указания к оформлению курсовых проектов. Изд. кафедры ТМ и

ДМ.-СПб.: ПИМаш, 1999.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: