Решение транспортной задачи методом потенциалов

Транспортная задача

Транспортная задача является одной из типичных задач линейного программирования. Она возникает при планировании наиболее рациональных перевозок груза. В одних случаях перевозки необходимо осуществлять так, чтобы были минимальны затраты времени, в других – чтобы были минимальны затраты по стоимости.

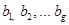Сформулируем транспортную задачу. Пусть в р пунктах отправления находится соответственно единиц однородного груза, который необходимо перевезти в g пунктов потребления в количестве . Известны стоимости (или время) перевозки единицы груза из пункта i в пункт j С_ij. Обозначим через 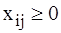количество единиц груза, перевозимого из i-го пункта отправления в j-ый пункт потребления. Суммарные затраты на перевозки выражаются соотношением:

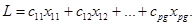
Переменные х_ij удовлетворяют ограничениям

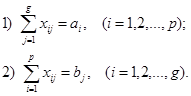(3)

Следовательно, требуется найти значения переменных х_ij, удовлетворяющие ограничениям 1), 2) и минимизирующие целевую функцию L.

 

Решение транспортной задачи состоит из двух этапов:

1. Определение исходного опорного решения.

2. Построение последовательных итераций, т. е. приближение к оптимальному решению и, в конечном итоге, получение оптимального решения.

На первом этапе для получения исходного опорного решения применяют либо метод “северо-западного угла”, либо метод минимальных стоимостей.

 

В методе “ северо-западного угла ” таблицу исходных данных заполняют, начиная с левого верхнего угла, двигаясь далее или по первой строке вправо или по первому столбцу вниз. В клетку (1,1) записывают меньшее из чисел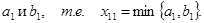

Если 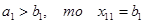и первый столбец “закрыт”, так как потребности потребителя В₁ полностью удовлетворены. Двигаясь далее по первой строке, в клетку (1,2) записывают меньшее из чисел .

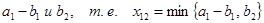Если 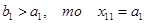и первая строка “закрывается”, так как исчерпаны запасы пункта А₁. В клетку (2,1) после этого записывают меньшее из чисел .

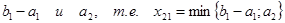Этот процесс продолжается до тех пор, пока на каком-то шаге не исчерпаются ресурсы а_p и потребности b_g.

На каждом шаге заполнения справа и снизу от таблицы отмечают остатки груза в пунктах отправки А_i и в пунктах потребления В_j.

Рассмотрим метод на конкретном примере.

Пример 4.

Пусть в пунктах отправления А₁, А₂, А₃ имеется соответственно 290, 310, 140 единиц груза. В пункты В₁, В₂, В₃ В₄ требуется соответственно 150, 100, 220, 270 единиц этого груза. Стоимости перевозок из пунктов А_i в пункты В_j задаются матрицей С:

.

Составить план перевозок по методу “северо-западного” угла, вычислить затраты.

Решение. Подготовим по исходным данным таблицу и заполним ее поэтапно, начиная с клетки (1,1). В столбце и строке, обозначенных через (0), помещены исходные количества груза для пунктов А₁, А₂, А₃, В₁, В₂, В₃, В_4.

 

Т а б л и ц а 3

	В1	В2	В3	В4	(0)	(1)	(2)	(3)	(4)	(5)
А1
А2
А3

 

(0) 150 100 220 270

(1) 0 100 220 270

(2) 0 0 220 270

(3) 0 0 180 270

(4) 0 0 0 270

(5) 0 0 0 140

 

 

В клетку (1,1) поместили

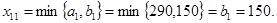
Тем самым на первом шаге полностью удовлетворены запросы пункта В₁, поэтому первый столбец таблицы после этого “закрыт”, т. е. все его остальные клетки (2,1), (3,1) заполняем нулями. Справа и снизу от таблицы просчитываем остатки после заполнения клетки (1,1). Эти остатки расположены в пунктах (1).

Так как на складе А₁ еще остался товар, 140 ед. груза, то переходим к заполнению клетки (1,2). Туда записываем, 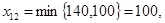чем полностью удовлетворяем запросы пункта В₂. Закрываем второй столбец и вычисляем остатки (2).

На складе А₁ все еще есть груз, 40 ед., поэтому заполняем клетку (1,3): 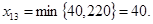Теперь запасы склада А₁ исчерпаны, поэтому “закроем” первую строку, записав в клетку (1,4) ноль. Вычислим остатки (3).

Так как запросы пункта В₃ удовлетворены частично, переходим к заполнению клетки (2,3): 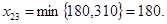Теперь на В₃ завезено столько груза, сколько требовалось, поэтому “закроем” третий столбец, полагая х₃₃=0. Вычислим остатки (4).

Переходим к заполнению клетки (2,4): Вычисляем остатки (5). Заполняем последнюю клетку таблицы (3,4)

Итак, со всех складов вывезен весь груз и полностью удовлетворены запросы пунктов В₁, В₂, В₃, В₄. По методу “северо-западного” угла получен следующий вариант перевозок: из пункта А₁ в В₁ завезти 150 ед. груза, из А₁ в В₂-100 ед., из А₁ в В₃ –40 ед.. Из пункта А₂ завезти в В₃ 180 ед. груза, из А₂ в В₄ –130 ед. Из пункта А₃ в В₄ –140 ед. груза.

При таком варианте перевозок будут следующие затраты:

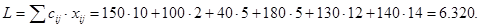Отыскание опорного плана перевозок по методу “северо-западного угла” никак не учитывает стоимостей перевозок.

 

Метод минимальных стоимостей состоит в том, что на каждом шаге построения опорного плана заполняют клетку с наименьшей стоимостью. Рассмотрим этот метод на конкретном примере.

Пример 5.

Найти опорный план перевозок методом минимальных стоимостей для исходных данных примера 4. Вычислить стоимость перевозки.

Решение.

Подготовим исходную таблицу, столбец и строчку, обозначенные через (0).

 

 

Т а б л и ц а 4

	В1	В2	В3	В4	(0)	(1)	(2)	(3)
А1
А2
А3

 

(0) 150 100 220 270

(1) 150 100 220 0

(2) 150 80 220 0

(3) 150 80 80 0

 

Так как наименьшая стоимость с₁₄=1, то заполнение таблицы начинаем с клетки (1,4): 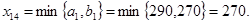Запросы пункта В₄ полностью удовлетворены, “закрываем” четвертый столбец, т. е. полагаем х₂₄=0, х₃₄=0. Вычисляем остатки (1).

Среди незаполненных клеток находим клетку с наименьшей стоимостью. Это клетка (1,2) так как с₁₂=2. Заполняем её Запасы пункта А₁ исчерпаны, поэтому “закроем” первую строку, положив х₁₁=0, х₁₃=0. Вычислим остатки (2).

Среди незаполненных клеток опять находим клетку с наименьшей стоимостью, это клетка (3,3). Полагаем 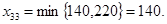Запасы пункта А₃ исчерпаны, “закрываем” третью строку нулями и находим остатки (3).

После этого шага у нас не остается выбора, так как груз остался только в пункте А₂. Заполним просто клетки (2,1), (2,2), (2,3) в соответствии с запросами В₁, В₂, В₃ (см. строчку (3)). В результате вся таблица заполнена, получили следующий вариант перевозки: из пункта А₁ в пункт В₂ необходимо перевезти 20 ед. груза, из А₁ в В₄-270 ед., из А₂ в В₁, В₂, В₃ соответственно 150, 80, 80 ед. Из А₃ в В₃ 140 ед. Вычислим затраты на такой вариант перевозки:

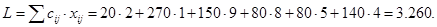Как видим, затраты в этом случае намного меньше, чем по варианту метода “северо-западного угла”.

 

Решение транспортной задачи методом потенциалов

Методом “северо-западного угла” или методом минимальных стоимостей получают первоначальное опорное решение поставленной задачи. В этом решении часть переменных является базисными (это те, в клетках которых в результате построения опорного плана получили ненулевые значения), а остальные - свободными (в клетках с их номерами нули). Так, например, в решении, полученном в примере 5 (таблица 4) переменные 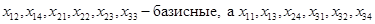-свободные.

Переход от исходного опорного решения к другим базисным решениям задачи методом потенциалов осуществляется следующим образом. Для базисных клеток таблицы составляются равенства

,

неизвестные пока величины u_i, v_j называют потенциалами, с_ij-заданные стоимости.

Совокупность таких соотношений для всех базисных клеток составляет совместную систему линейных уравнений, причем значение одной из неизвестных задают произвольно, тогда значения остальных потенциалов находятся однозначно.

После определения значений потенциалов u_i и v_j для небазисных клеток вычисляют числа ,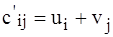

которые называют фиктивными стоимостями (в отличие от настоящих). Затем находят разности .

Если все разности неотрицательны, то исходное решение оптимальное. Если среди них есть отрицательные, то переходят к новому базисному решению.

Базисной назначают ту переменную, для которой (если таких несколько, то выбирают наименьшую). При этом должны сохраняться ограничения (3) и количество нулевых переменных в базисном решении.

По выбранной новой базисной переменной х_ij организуют цикл балансового пересчета. Для этого в клетку, соответствующую переменной х_ij, записывают некоторое число λ>0, после чего из каких-то выбранных базисных клеток i-ой строки и j-го столбца вычитают λ (для того чтобы сохранялись суммы по i-ой строке и j-му столбцу). Затем пунктирной линией строят прямоугольник, в одной из вершиной которого клетка х_ij (число λ) и в противоположной к ней по диагонали вершине прибавляют число λ.

 

 

 

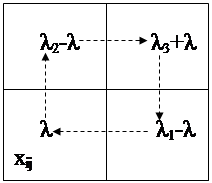Заметим, что λ>0 подбирают так, чтобы

,

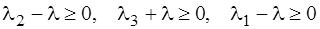причем одно из них должно быть обязательно равно нулю.

Отметим, что балансовый пересчет не всегда осуществляют по прямоугольнику, иногда обходят клетки по более сложной замкнутой ломаной линии, в одной из вершин которой находится х_ij, а в остальных вершинах–базисные переменные.

Пример 6

Найти оптимальное решение задачи, сформулированной в примере 4. В качестве опорного решения взять решение, полученное методом минимальных стоимостей в примере 5.

Решение. Исходное опорное решение, полученное методом минимальных стоимостей, имеет следующий вид:

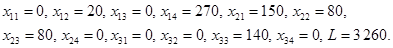
Ненулевые переменные (х₁₂, х₁₄, х₂₁, х₂₂, х₂₃, х₃₃) являются базисными. Для нахождения потенциалов составим и решим систему

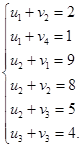
Значение одного из неизвестных зададим произвольно, пусть, например, u₁=0. Тогда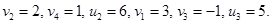

Вычислим фиктивные стоимости для небазисных переменных:

Найдем разности

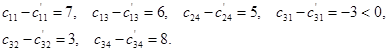
Так как 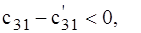то новой базисной переменной становится х₃₁. Для балансового пересчета составим по таблице 4 (примера 5) прямоугольник, одна из вершин которого будет клетка, соответствующая х₃₁. Три другие вершины должны находиться в клетках с базисными переменными (т. е. с ненулевыми значениями). Ими, очевидно, будут клетки, соответствующие х₂₁, х₂₃, и х₃₃.

Полагаем х₃₁=λ. Суммы значений переменных по строкам и столбцам должны оставаться неизменными, поэтому проводим следующий балансовый пересчет.

 

 

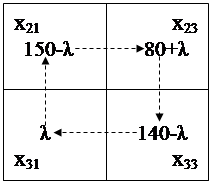Новые значения должны удовлетворять следующим условиям:

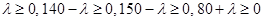, причем одно из последних трех должно быть равно нулю (для сохранения количества базисных и свободных переменных). Поэтому полагаем 140-λ=0 и находим

.

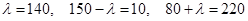Получили новое базисное решение.

Т а б л и ц а 5

	В1	В2	В3	В4
А1
А2
А3

 

Значение целевой функции при таком решении следующее

.

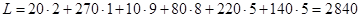Составим систему и найдем потенциалы для этого решения

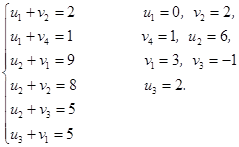
Вычислим фиктивные стоимости и разности .

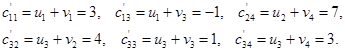
Найдем разности

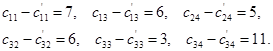
Поскольку все разности неотрицательны, то найденное решение оптимальное. Итак, целевая функция рассматриваемой транспортной задачи принимает наименьшее значение L=2840 при следующих значениях переменных.

Иначе говоря, со склада А₁ следует 20 ед. груза перевезти в пункт В₂ и 270 ед. – в пункт В₄. Со склада А₂ 10 ед. груза в пунктВ₁, 80 ед. в пункт В₂ и 220 ед. в пункт В₃. Все запасы склада А₃, 140 ед. груза, следует перевезти в пункт В₁. Расходы на такой вариант перевозки будут минимальными и составят 2840 единиц.

 

Контрольные вопросы

1. В чем состоит основная задача линейного программирования?

2. В чем заключается геометрический метод решения задач линейного программирования?

3. При каком количестве переменных применяют геометрический метод?

4. Какую прямую называют опорной прямой?

5. Какое решение задачи линейного программирования называется допустимым? Оптимальным?

6. Можно ли применять симплекс-метод сразу же, без предварительной подготовки, для решения задачи на нахождение наименьшего значения целевой функции?

7. Какая форма называется канонической формой задачи линейного программирования?

8. Каким образом можно преобразовать неравенства системы ограничений к равенствам?

9. Какое решение называется опорным решением при применении симплекс-метода?

10. Какую строку назначают опорной строкой в симплекс-таблице?

11. Какой столбец назначают опорным столбцом в симплекс-таблице?

12. Какая строка симплекс-таблицы называется оценочной?

13. Каково условие оптимальности решения (по симплекс-таблице)?

14. Каково условие неразрешимости задачи (по симплекс-таблице)?

15. В чем заключается транспортная задача?

16. Какое решение транспортной задачи называют опорным?

17. Какими методами получают опорное решение транспортной задачи?

18. Можно ли получить оптимальное решение методом северо-западного угла?

19. Всегда ли получается оптимальное решение методом минимальных стоимостей?

20. По какой методике заполняют таблицу в методе северо-западного угла?

21. По какой методике заполняют таблицу в методе минимальных стоимостей?

22. В чем заключается метод потенциалов?

23. Каков критерий оптимальности решения по методу потенциалов?

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Задание 1

Завод организует производство двух новых видов облицовочного кирпича. Стоимость одного кирпича первого и второго вида соответственно равна с₁ и с₂.

Если обозначить через х_i, (i=1,2) число выпускаемых за сутки кирпичей, то суточная прибыль предприятия будет определяться функцией:

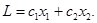
Известно, что для производства одного кирпича первого вида требуется три вида сырья в количестве соответственно а₁, а₂, а₃ единиц. Для производства одного кирпича второго вида также необходимо использовать то же самое сырье в количестве - в₁, в₂, в₃ единиц.

Суммарные запасы сырья, которое может быть использовано за сутки предприятием, составляют S₁, S₂, S₃ единиц.

Организовать производство таким образом, чтобы прибыль была максимальной.

Таким образом, требуется найти наибольшее значение функции при следующих ограничениях на переменные:

.

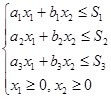Решить задачу геометрическим и симплекс-методом, учитывая следующие данные:

n– индивидуальный номер варианта студента, равный последней цифре номера зачетной книжки.

 

 

Вариант 1 (группа ЗМПГС-101)

 

 

Вариант 2 (группа ЗМПГС-102)

 

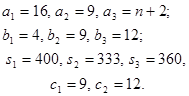
Вариант 3 (ЗМПГС-103)

 

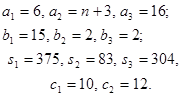
Задание 2

На трех складах А₁, А₂, А₃ имеется соответственно а₁, а₂, а₃ тонн стройматериалов. Требуется их доставить на четыре стройки В₁, В₂, В₃, В₄ в количестве в₁, в₂, в₃, в₄ тонн. Время на перевозку одной тонны стройматериалов из пункта А_i на стройку В_j задается матрицей

.

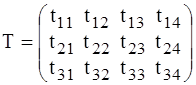1) Методом минимальных стоимостей найти время, необходимое на перевозку всех материалов.

2) Методом потенциалов получить оптимальное решение задачи, при котором затраты времени на все перевозки минимальны.

Примечание: Выполнение задания 1) в этой задаче обязательно для всех. Выполнение задания 2)– по желанию студента.

n– индивидуальный номер варианта студента, равный последней цифре номера зачетной книжки.

Вариант 1 (101)

Вариант 2 (102)

Вариант 3 (103)

Поделиться:

Воспользуйтесь поиском по сайту: