Проверка гипотез о взаимосвязи переменных

Рассмотрим некоторые статистики, обычно используемые для оценки статистической значимости и тесноты связи переменных, содержащихся в таблице сопряженности.

Статистическая значимость наблюдаемой связи обычно измеряется критерием . Подробный пример применения этого критерия для проверки взаимосвязи переменных рассмотрен в главе «Одномерные статистики и проверка гипотез».

Критерий помогает определить наличие или отсутствие систематической связи между двумя переменными. В данном случае нулевая гипотеза Но утверждает, что между двумя переменными не существует никакой связи. Проверка нулевой гипотезы выполняется вычислением частот распределения признаков анализируемых переменных в ячейках таблицы, которые можно было бы ожидать, если бы не существовало зависимости между переменными, и при данных итоговых числах в каждом ряду и колонке. Затем для вычисления значения эти ожидаемые частоты, обозначаемые , сравнивают с фактически наблюдаемыми частотами распределения признаков , соответствующими ячейкам таблицы. Чем больше разница между ожидаемыми и фактическими частотами, тем выше значение статистики.

Статистику также можно использовать в проверках степени согласия, чтобы определить, согласуется ли определенная модель с наблюдаемыми данными. Эти проверки выполняют вычислением уровня статистической значимости выборочных отклонений от предполагаемых теоретических (ожидаемых) распределений, а также можно выполнить как на основе таблиц сопряженности, так и на основе таблиц распределения частот.

В качестве общего правила стоит запомнить, что проверку по критерию нельзя выполнять, если ожидаемые или теоретические частоты в любой из ячеек меньше пяти. Если число наблюдений в любой ячейке меньше десяти, или если таблица имеет два ряда и две колонки (таблица 2х2), то необходимо использовать поправочный коэффициент.

На практике проведение перекрестной табуляции полезно вести по следующим этапам.

1. Проверьте нулевую гипотезу о том, что отсутствует связь между переменными, используя критерий . Если вам не удалось отклонить нулевую гипотезу, то связь между переменными отсутствует.

2. Если нулевая гипотеза Но отклонена, то определите тесноту связи, используя подходящие статистики (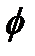 -коэффициент, коэффициент сопряженности, коэффициент λ или другие статистики).

-коэффициент (phi coefficient) используют для измерения тесноты связи при анализе таблицы с двумя рядами и двумя колонками (таблица 2х2). Он пропорционален корню квадратному из . -коэффициент принимает значение, равное 0, если связь отсутствует, на что также указывает и значение , равное 0. При сильной связи между переменными -коэффициент имеет значение 1 и все наблюдения находятся на главной или второстепенной диагонали.

Коэффициент сопряженности признаков (contingency coefficient) используют для оценки тесноты связи в таблицах любого размера. Значения коэффициента сопряженности находятся в диапазоне от 0 до 1. При отсутствии связи он равен нулю (т.е. переменные статистически независимы), но своего максимального значения (1) он никогда не достигает.

Коэффициент λ используется в том случае, когда переменные измерены с помощью номинальной шкалы. Асимметрический коэффициент «лямбда» (asymmetric lambda) выражает меру выраженного в процентах улучшения прогнозирования значения зависимой переменной при данном значении независимой переменной. Значения коэффициента λ лежат в пределах от 0 до 1. Значение λ, равное 0, означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая категория независимой переменной связана с одной категорией зависимой переменной.

Симметричный коэффициент λ не дает предположения о том, какая из переменных зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в обоих направлениях.

3. Если нулевая гипотеза Но отклонена, то поясните характер связи, вычислив проценты в направлении независимой переменной через зависимую переменную.