В чем основной смысл леммы Брента?

Распараллеливание вычислений функции

Вариант 4

Исходное выражение:

(s – d)/(f + g)*(h – j)*(k + 1)+(c + v + b+ n*m)

 

Эквивалентное выражение:

(((s – d)/(f + g))*((h – j)*(k + l)))+((c+(v + b))+(n*m))

 

 

Дерево вычислений для эквивалентного выражения:

 

 

Характеристики дерева:

· Общее число операций w=12

· Число ярусов h=5

· Время на вычисление арифметического выражения t=h=5

· Число вычислителей, необходимых для реализации данного вычисления p=6

· Средняя степень параллелизма D=6/5=1,2

· Ускорение S=12/5=2,4

· Эффективность E=12/30=0,4

 

Оптимизированное вручную дерево вычислений для эквивалентного выражения:

 

 

Характеристики дерева:

· Общее число операций w=12

· Число ярусов h=5

· Время на вычисление арифметического выражения t=h=5

· Число вычислителей, необходимых для реализации данного вычисления p=4

· Средняя степень параллелизма D=4/5=0,8

· Ускорение S=12/5=2,4

· Эффективность E=12/20=0,6

 

Эффективность оптимизированного вручную дерева выше эффективности дерева вычислений для эквивалентного выражения

Работа с приложением по распараллеливанию арифметических выражений

S		1,714		2,4	2,4	2,4	2,4	2,4	2,4	2,4
E		0,857	0,666	0,6	0,48	0,4	0,342	0,3	0,266	0,24

График зависимости Эффективности E и ускорения S от количества процессоров:

 

Проверка Леммы Брента:

W=12;

P = 1; T_p = H_p = 12; D_p = 1; S_p = 1; E_p = 1;

P = 2; T_p = H_p = 7; t_min =5; Лемма Брента: t`= 5 + (12-5)/2 = 8,5 (Лемма выполняется)

P = 3; T_p = H_p = 6; t_min =5; Лемма Брента: t`= 5 + (12-5)/3 = 7,3 (Лемма выполняется)

P = 4; T_p = H_p = 5; t_min =5; Лемма Брента: t`= 5 + (12-5)/4 = 6,8 (Лемма выполняется)

P = 5; T_p = H_p = 5; t_min =5; Лемма Брента: t`= 5 + (12-5)/5 = 6,4 (Лемма выполняется)

P = 6; T_p = H_p = 5; t_min =5; Лемма Брента: t`= 5 + (12-5)/6 = 6,2 (Лемма выполняется)

 

Вычисление значения полинома по схеме Горнера при помощи разложения схемы по методу циклической редукции

S₆=(((((d₀a₁ + d₁)*(a₂ + d₂)*a₃ + d₃)*a₄ + d₄)*a₅ + d₅)*a₆ + d₆

S₆ = S₄ * a₆⁽¹⁾ + d₆⁽¹⁾ = S₄ * a₅ * a₆ + d₅ * a₆ + d₆

S₄ = S₂ * a₄⁽¹⁾ + d₄⁽¹⁾ = S₂ * a₃ * a₄ + d₃ * a₄ + d₄

S₂ = S₀ * a₂⁽¹⁾ + d₂⁽¹⁾ = S₀ * a₁ * a₂ + d₁ * a₂ + d₂

S₀ = d₀

S₆ = ((d₀ * a₁ * a₂ + d₁ * a₂ + d₂)*a₃ * a₄ + d₃ * a₄ + d₄)* a₅ * a₆ + d₅ * a₆ + d₆

 

_{Неоптимизированное дерево}

 

 

W = 15

T₁ = 11

T_p = h = 6

P = 6

 

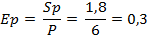
Оптимизированное дерево

 

W = 15

T₁ = 7

T_p = h = 6

P = 2

 

 

Ответы на контрольные вопросы

Какой принцип распараллеливания используется при распараллеливании арифметических выражений?

Наиболее известные алгоритмы распараллеливания арифметических выражений основаны на общем принципе: ориентированный ациклический граф, описывающий последовательное вычисление выражения E, представляет собой, в силу свойства, бинарное дерево. К этому дереву применяются преобразования в соответствии с законами коммутативности, ассоциативности и дистрибутивности. В резуль­тате бинарное дерево трансформируется в ориентированный ациклический граф , соответствующий выражению Ẽ, эквивалентному E.

 

Порядок вычисления может быть перераспределен или доопределен таким образом, что бы некоторые операции можно было выполнять параллельно. Поэтому говорят, что выражения обладают неявным параллелизмом.

 

Какие основные свойства арифметических операций используются при преобразовании арифметических выражений в эквивалентные?

Два выражения E и Ẽ называются эквивалентными (E ~ Ẽ) в том и только в том случае, если выражение E преобразуется в Ẽ и наоборот, путем использования конечного числа раз законов ассоциативности, коммутативности и дистрибутивности.

 

Какие характеристики параллельности Вы знаете?

степень параллелизма, ускорение и эффективность параллельных алгоритмов.

 

Чем характеризуется эффективность схемы при оптимальной загрузке процессоров?

Количеством задействованных процессоров, загруженностью процессоров на каждом этапе вычислений, временем выполнения вычислений и отношениям ускорения вычислений к количеству процессоров.

 

В чем основной смысл леммы Брента?

Данное утверждение позволяет, зная характеристики арифметического выражения при распараллеливании на неограниченном числе процессоров, оценить время реализации выражения на ограниченном числе вычислителей.

 

Поделиться:

Воспользуйтесь поиском по сайту: