 |
Работа № 1. Виртуальный логический конвертор (Logic converter)
|
|
|
|
Цель: Изучение назначения и принцип работы виртуального устройства логического конвертора (преобразователя). Знакомство с базовыми функциями логического конвертора.
Оборудование: Электронная лаборатория Electronics Workbench.
Краткая теория
 |
Теперь для решения предложенных выше задач воспользуемся программой электронной лаборатории Electronics Workbench. Для построения логических схем в библиотеке Logic Gates (логические элементы) предусмотрено возможность выбора логических элементов. На рис. 9 перечень выбора возможных логических элементов.
Рис. 9
 |
На рис. 10 показаны обозначения, используемые в Electronics Workbench логических элементов: конъюнкции - И, дизъюнкции – или, отрицания –НЕ, 2 – И – НЕ, 2 –ИЛИ – НЕ.
Рис. 10.
В электронной лаборатории Electronics Workbench имеется виртуальное устройство. Логический конвертор (Logic Converter) позволяет осуществлять 6 логических преобразований для логической функции с числом переменных от 1 до 8: представление таблицы истинности собранной из логических элементов схемы; обращение таблицы истинности в логическую формулу (СДНФ); минимизацию СДНФ; обращение формулы в таблицу истинности; представление формулы в виде схемы в логическом базисе 2-И-НЕ. Логический конвертор выбирается из меню Instruments (рис. 11).
 |
Рис. 11
Приведем описание технологии исследования логических схем с помощью логического конвертора (преобразователя).
1. Собираем логическую схему.
2. Подключаем исследуемую логическую схему к логическому конвертору (входов 8, выход один – расположен справа).
3. Открываем логический конвертор щелчком левой кнопкой мыши по иконке конвертора. На экране появляется меню Logic Converter (рис. 12).
|
|
|
4.
 |
Для получения таблицы истинности нажимаем
5.
 |
Для получения логической функции (структурной формулы) нажимаем
С помощью логического конвертора можно проводить не только анализ логических устройств, но их синтез.
Приведем описание технологии синтеза логического устройства по выходной комбинации с помощью логического конвертора (преобразователя).
1.
 |
Раскрываем лицевую панель логического конвертора (рис. 12).
Рис. 12
2. Активизируем курсором клеммы-кнопки A, B,..H (начиная с F), количество которых равно количеству входов синтезируемого устройства (количеству логических переменных).
3. Вносим необходимые изменения в столбец OUT и после нажатия на клавиши на панели преобразователя получаем результат в виде схемы на рабочем поле программы и логическую функцию в дополнительном дисплее.
Задача 3. Проведите анализ логического устройства (рис. 13) по функциональной схеме с помощью Electronics Workbench.

Рис. 13
На рис. 14 решение задачи в Electronics Workbench.
Контрольные вопросы и задания
1. Объяснить назначение и принцип работы логического конвертора. Решить следующие задания с использованием логического конвертора.
 |
|
2. Исследуйте следующие функциональные схемы.

 |
3. Исследуйте логическую схему и постройте функциональную логическую схему: а) B*C’+A*C.
б) A*B’C+A*B’*C’+A’*B’*C.
с) A*(B+C)*(D+C).
4.Провидите синтез логического устройства с выходной комбинацией:
а) 00100111.
б) 01101001.
с) 0110100110010110.
Работа № 2.Цифровой компаратор
Цель: Изучение назначения устройства и принцип работы цифрового компаратора.
Оборудование: Электронная лаборатория Electronics Workbench.
Краткая теория
Цифровые компараторы (от английского compare – сравнивать) выполняют сравнение двух чисел А, В одинаковой разрядности, заданных в двоичном или двоично-десятичном коде. В зависимости от схемного исполнения компараторы могут определять равенство А=В или неравенства А<B,A>B. Результат сравнения отображается в виде логического сигнала на одноименных выходах, в случае выполнения условия на выходе 1.
|
|
|
Цифровые компараторы применяются для выявления нужного числа (слова) в цифровых последовательностях, для выполнения условных переходах.
Схемы одноразрядных компараторов приведены на рис. 15, 16, 17..

Рис. 15
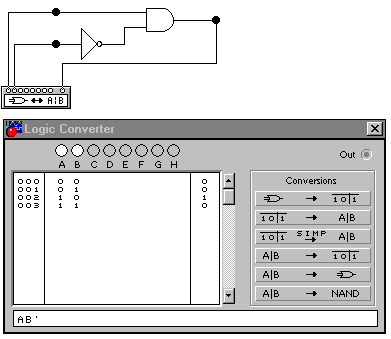
Рис. 16

Рис. 17
Операциям сравнения (A<B, A=B, A>B) соответствуют структурные формулы (A’*B, A’*B’+A*B, A*B’).
Условно обозначим логические схемы компараторов:
 |
Тогда, компараторы =>, <=, <> будут выглядеть следующим образом:
 |  | |||||
 | ||||||
 |

 где элемент отрицания.
где элемент отрицания.
Логические функции этих компараторов выглядят:
(A’*B)’, (A*B’)’, (A’*B’+A*B)’.
Можем упростить данные формулы с помощью законов алгебры логики:
(A’*B)’=A’’+B’=(закон де Моргана)=A+B’ (закон двойного отрицания),
(A*B’)’=A’+B’’=A’+B,
(A’*B’+A*B)’=(A’’+B’’)*(A’+B’)=(A+B)*(A’+B’).
Таблицы истинности для данных формул:
| A | B | B’ | A+B’ (A=>B) | A’ | A’+B (A<=B) | A+B | A’+B’ | (A+B)*(A’+B’) (A<>B) |
Контрольные вопросы и задания
1. Какие функции выполняет цифровой компаратор, в каких устройствах он может быть использован?
2. Подсоединив схемы к логическому конвектору, исследуйте приведенные схемы.
3. Составьте схему устройства, объединяющую все три компаратора.
4. Составьте схемы устройств, удовлетворяющие условиям: A<=B, A<>B, A>=B.
5. Исследуйте составленные схемы устройств.
6.Составьте структурные формулы и таблицы истинности для составленных выше логических схем цифровых компараторов.
|
|
|


