 |
обучающихся по направлению «Менеджмент»
|
|
|
|
Вопросы к экзамену по дисциплине
«Математика»
Для студентов 1 курса бакалавриата,
обучающихся по направлению «Менеджмент»
(II семестр, 2015-2016 уч. год)
1. Числовые последовательности. Способы задания последовательностей. Прогрессии.
2. Предел последовательности и его свойства. Единственность предела. Ограниченность сходящейся последовательности.
3. Переход к пределу в неравенствах, теорема о трех последовательностях. Бесконечно малые и бесконечно большие последовательности, их свойства. Свойства пределов, связанные с арифметическими действиями.
4. Монотонные последовательности. Теорема Вейерштрасса о существовании предела монотонной ограниченной последовательности. Число e.
5. Предел функции. Различные типы пределов: односторонние пределы, пределы в бесконечности, бесконечные пределы.
6. Бесконечно малые и бесконечно большие функции, их свойства.
7. Свойства пределов, связанные с арифметическими действиями и с неравенствами. Замена переменной при вычислении предела (предел сложной функции).
8. Сравнение бесконечно малых функций: эквивалентные функции.
9. Первый и второй замечательные пределы.
10. Непрерывность функции в точке. Непрерывность суммы, разности, произведения и частного непрерывных функций. Непрерывность сложной и обратной функции.
11. Непрерывность элементарных функций. Теорема о сохранении знака непрерывной функции. Точки разрыва функции, их классификация.
12. Свойства функций, непрерывных на отрезке: теоремы о существовании корня, о промежуточных значениях, об ограниченности функции, о достижении наибольшего и наименьшего значений.
|
|
|
13. Производная функции. Дифференцируемость и дифференциал функции. Непрерывность дифференцируемой функции.
14. Правила дифференцирования суммы, разности, произведения и частного двух функций, сложной и обратной функций. Производные основных элементарных функций.
15. Геометрический смысл производной и дифференциала функции. Уравнение касательной к графику функции.
16. Правило Лопиталя раскрытия неопределенностей.
17. Производные и дифференциалы высших порядков.
18. Признак монотонности функции на интервале. Достаточное условие локального экстремума.
19. Выпуклые (вогнутые) функции. Достаточные условия выпуклости функции. Необходимый и достаточный признаки точки перегиба.
20. Асимптоты графика функции. Общая схема исследования функции и построения ее графика.
21. Отыскание наибольшего и наименьшего значений функции на отрезке.
22. Первообразная и неопределенный интеграл. Таблица неопределенных интегралов.
23. Свойства неопределенного интеграла. Замена переменной в неопределенном интеграле, интегрирование по частям.
24. Определенный интеграл (по Риману) и его свойства. Интегрируемость непрерывной функции.
25. Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница.
26. Замена переменной в определенном интеграле, интегрирование по частям.
27. Геометрические приложения определенного интеграла: вычисление площади криволинейной трапеции.
28. Несобственные интегралы.
29. Функции нескольких переменных. Поверхности (линии) уровня функции.
30. Предел и непрерывность функции нескольких переменных. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.
|
|
|
31. Частные производные, дифференцируемость, дифференциал функции нескольких переменных. Достаточное условие дифференцируемости. Непрерывность дифференцируемой функции.
32. Частные производные высших порядков. Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
33. Условный экстремум функции нескольких переменных. Метод исключения переменных. Метод множителей Лагранжа.
34. Эмпирические формулы и метод наименьших квадратов.
35. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.
36. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости.
37. Числовые ряды с неотрицательными членами: критерий и признаки сходимости (первый и второй признаки сравнения, признак Даламбера в предельной форме, интегральный признак).
38. Знакочередующиеся ряды. Признак Лейбница. Оценка остатка ряда.
39. Абсолютно и условно сходящиеся числовые ряды. Свойства абсолютно и условно сходящихся рядов.
40. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда. Свойства степенного ряда на интервале сходимости.
41. Ряды Тейлора (Маклорена). Разложимость в ряд Тейлора бесконечно дифференцируемой функции с производными, ограниченными в совокупности. Разложения функций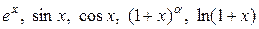 
в ряд Маклорена.
42. Обыкновенные дифференциальные уравнения первого порядка, их решения. Нормальная форма уравнения первого порядка. Задача Коши.
43. Теорема о существовании и единственности решения задачи Коши для уравнения первого порядка в нормальной форме. Общее и частное решения уравнения. Общий интеграл. Особые решения.
44. Уравнения первого порядка, интегрируемые в квадратурах: с разделяющимися переменными, однородные, линейные.
|
|
|
