 |
Изгиб упругих пластинок. Метод Ритца–Тимошенко.
|
|
|
|
Сущность вариационных методов решения задач теории изгиба пластинок заключается в приведении основного дифференциального уравнения в частных производных С.Жермен-Лагранжа к системе линейных алгебраических уравнений или к обыкновенному дифференциальному уравнению.
Для приведения основного дифференциального уравнения изгиба пластинки к системе линейных алгебраических уравнений, приближенное значение функции прогибов 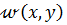 можно выбирать в виде ряда с конечным числом членов:
можно выбирать в виде ряда с конечным числом членов:
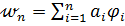 , (7.2.1)
, (7.2.1)
где  - линейные независимые фукции, удовлетворяющие граничным условиям задачи;
- линейные независимые фукции, удовлетворяющие граничным условиям задачи;  постоянные параметры, подлежащие определению.
постоянные параметры, подлежащие определению.
В зависимости от числа членов ряда (7.2.1) решение может быть получено с любой степенью точности.
Постоянные параметры  выбирают из условий, чтобы функция (7.2.1) по возможности точнее представляла искомую функцию
выбирают из условий, чтобы функция (7.2.1) по возможности точнее представляла искомую функцию 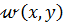 . Из различных методов отыскания постоянных параметров
. Из различных методов отыскания постоянных параметров  рассмотрим два: метод Ритца–Тимошенко и метод Бубнова–Галеркина, которые относятся к прямым вариационным методам.
рассмотрим два: метод Ритца–Тимошенко и метод Бубнова–Галеркина, которые относятся к прямым вариационным методам.
Метод Ритца первоначально был изложен Рэлеем (Дж. Уильям Стрэтт) для теории звука в 1877 г. и математически обоснован и развит Вальтером Ритцем в 1908 г.; С.П. Тимошенко называет его «метод Рэлея-Ритца», сейчас он больше известен как метод Ритца – Тимошенко.
Метод Ритца–Тимошенко основан на использовании известного из курса теоретической механики принципа возможных перемещений: для того, чтобы система, подчиненная идеальным удерживающим связям, находилось в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к ней сил на всяком возможном перемещении равнялась нулю.
Рассматривая отдельно действие внешних и внутренних сил, принцип возможных перемещений можно представить следующим образом:
|
|
|
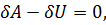 (а)
(а)
где: 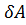 - возможная работа внешних сил (объемных и поверхностных) на каком-либо возможном перемещении;
- возможная работа внешних сил (объемных и поверхностных) на каком-либо возможном перемещении;
 - возможная работа внутренних сил, представляющая собой приращение потенциальной энергии на том же возможном перемещении с обратным знаком.
- возможная работа внутренних сил, представляющая собой приращение потенциальной энергии на том же возможном перемещении с обратным знаком.
Пусть тело находится в равновесии под действием объемных сил, составляющие которых X, Y, Z, и поверхностных сил 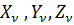 . Дадим частицам тела возможные перемещения, составляющие которых
. Дадим частицам тела возможные перемещения, составляющие которых  , и подсчитаем работу внешних сил на этих возможных перемещениях. Элементарная работа составляющей объемных сил Х, приходящейся на единицу объема, равна произведению этой силы на объем бесконечного малого элемента
, и подсчитаем работу внешних сил на этих возможных перемещениях. Элементарная работа составляющей объемных сил Х, приходящейся на единицу объема, равна произведению этой силы на объем бесконечного малого элемента 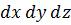 и на возможное перемещение
и на возможное перемещение 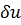 в направлении этой силы:
в направлении этой силы:
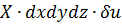 .
.
Точно так же элементарные работы составляющих объемных сил Y и Z равны соответственно:

Работа, производимая объемными силами во всем объеме тела V, равна интегралу по этому объему от суммы элементарных работ, совершаемых каждой из составляющих объемной силы:
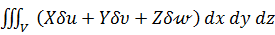 (б)
(б)
Элементарная работа составляющей поверхностных сил  , которая действует на бесконечно малом элементе поверхности ds, равна произведению равнодействующей этой составляющей на площадке ds на возможное перемещение
, которая действует на бесконечно малом элементе поверхности ds, равна произведению равнодействующей этой составляющей на площадке ds на возможное перемещение 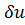 в направлении этой составляющей:
в направлении этой составляющей:

Аналогично определяются и элементарные работы двух других составляющих поверхностных сил:

Работа, производимая поверхностными силами, действующими на всей поверхности тела s, равна интегралу по всей поверхности тела от суммы элементарных работ, совершаемых каждой из составляющих поверхностных сил:
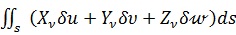 . (в)
. (в)
Таким образом, возможная работа всех внешних сил на возможных перемещениях равна суме работ объемных (б) и поверхностных (в) сил:
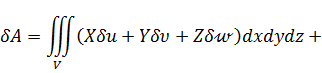
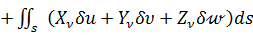 (г)
(г)
При вычислении возможной работы внешних сил варьировались только перемещения  , а поверхностные силы оставалась постоянными, поэтому оператор
, а поверхностные силы оставалась постоянными, поэтому оператор  в формуле (г) можно вынести из-под знаков интегралов, сделав общим для обоих интегралов:
в формуле (г) можно вынести из-под знаков интегралов, сделав общим для обоих интегралов:
|
|
|
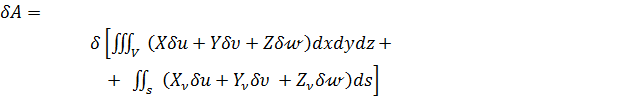 (д)
(д)
Приращение потенциальной энергии 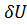 в формуле (а) подсчитывается согласно интегралу:
в формуле (а) подсчитывается согласно интегралу:
 , (е)
, (е)
где 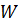 - удельная потенциальная энергия, определяемая по формуле Клапейрона
- удельная потенциальная энергия, определяемая по формуле Клапейрона
W = 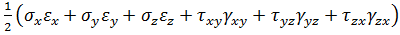 .
.
Представляя в соотношении (а) оператор  общим для обоих слагаемых, получаем:
общим для обоих слагаемых, получаем:
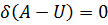 . (ж)
. (ж)
Выражение, стоящее в скобках, представляет собой работу всех внешних и внутренних сил, приложенных к телу. Эта величина с обратным знаком является потенциальной энергией системы внешних и внутренних сил, действующих на упругое тело:
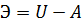 .(7.2.2)
.(7.2.2)
Вводя это обозначение, вместо условия (ж) получаем следующее соотношение:
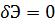 . (з)
. (з)
Так как первая вариация δ с точностью до бесконечно малых величин высшего порядка равна первому дифференциалу, то вместо условия (з) можно написать
 ,
,
а это условие означает, что потенциальная энергия системы Э имеет экстремальное значение.
В курсе теоретической механики доказывается теорема Лагранжа – Дирихле, на основании которой можно сформулировать следующий принцип минимума потенциальной энергии: из всех возможных перемещений упругого тела перемещения, удовлетворяющие условиям устойчивого равновесия, сообщают потенциальной энергии системы минимального значения.
Таким образом, потенциальная энергия системы (7.2.2):
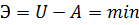 , (7.2.3)
, (7.2.3)
где потенциальная энергия  , накапливаемая в упругом теле, определяется по формуле, полученной интегрированием по всему объему тела V формулы Клапейрона:
, накапливаемая в упругом теле, определяется по формуле, полученной интегрированием по всему объему тела V формулы Клапейрона:
U = 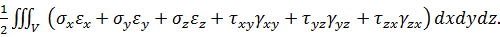 (7.2.3а)
(7.2.3а)
Для изгибаемых пластинок, защемленных по произвольному контуру, или прямоугольных шарнирно опертых по всем сторонам,формула (7.2.3а) упрощается:
U= 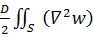 2dxdy, (7.2.3б)
2dxdy, (7.2.3б)
где D – цилиндрическая жесткость пластинки: D=Eh3/12(1-μ2), а двойной интеграл берется по всей площади срединной поверхности пластинки.
Работа объемных и поверхностных сил 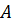 согласно формуле (д):
согласно формуле (д):
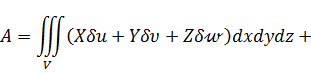
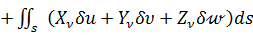 (и)
(и)
При изгибе пластинки объемными силами пренебрегают, а из составляющих поверхностных сил отлична от нуля только одна:
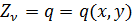 .
.
Подставляя это выражение в формулу (и) и выбирая элемент поверхности ds в виде прямоугольника со сторонами dx и dy, получаем работу внешних сил при изгибе пластинки:
|
|
|
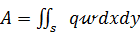 (7.2.4)
(7.2.4)
Если приближенное значение функции прогибов выбирать в виде ряда (7.2.1), то после подстановки этого значения в формулу (7.2.3) потенциальная энергия системы окажется функцией параметров  :
:
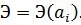
Чтобы найти значения параметров  , соответствующие минимуму потенциальной энергии системы, нужно приравнять нулю частные производные:
, соответствующие минимуму потенциальной энергии системы, нужно приравнять нулю частные производные:
 (7.2.5)
(7.2.5)
Производная квадратичной функции параметров  оказывается линейной функцией этих параметров, поэтому соотношения (7.2.5) представляют собой систему
оказывается линейной функцией этих параметров, поэтому соотношения (7.2.5) представляют собой систему 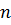 линейных уравнений с
линейных уравнений с 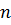 неизвестными параметрами
неизвестными параметрами  .
.
Таким образом, метод Ритца–Тимошенко позволяет заменить задачу о нахождении решения дифференциального уравнения С.Жермен-Лагранжа задачей о нахождении минимума потенциальной энергии. Такая замена возможна в связи с тем, что как дифференциальное уравнение изгиба пластинки, так и вариационное уравнение (з) являются уравнениями равновесия упругого тела.
Рассматривая вариационное уравнение (з) в форме
 , (к)
, (к)
внесем в него выражения потенциальной энергии (7.2.3а), формулу приращения удельной потенциальной энергии Клапейрона, а также возможную работу всех внешних сил (г), и учтем, что вариация геометрических уравнений Коши дает
 ,
,
……… …… …… ……
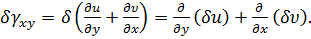
… ……… ……… …… …..
В результате преобразований, опущенных из-за громоздкости, получим вместо (з) уравнение, в котором возможные перемещения 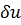 ,
, 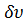 ,
,  ничем между собой не связаны; поэтому, чтобы последнее уравнение обращалось в тождество при любых значениях возможных перемещений, должны обращатся в нуль коэффициенты при этих возможных перемещениях. Таким образом, получим шесть уравнений: три уравнения представляют собой статические условия на поверхности в напряжениях(7.5), а три уравнения – дифференциальные уравнения равновесия (7.2). Следовательно, вариационное уравнение (к) заключает в себе дифференциальные уравнения равновесия (7.2) и статические граничные условия (7.5). Отсюда следует, что при использовании вариационного уравнения (к) для приближенного решения задач при выборе функции φi обязательными являются только геометрические граничные условия, а статические граничные условия и дифференциальное уравнение задачи удовлетворяются автоматически.
ничем между собой не связаны; поэтому, чтобы последнее уравнение обращалось в тождество при любых значениях возможных перемещений, должны обращатся в нуль коэффициенты при этих возможных перемещениях. Таким образом, получим шесть уравнений: три уравнения представляют собой статические условия на поверхности в напряжениях(7.5), а три уравнения – дифференциальные уравнения равновесия (7.2). Следовательно, вариационное уравнение (к) заключает в себе дифференциальные уравнения равновесия (7.2) и статические граничные условия (7.5). Отсюда следует, что при использовании вариационного уравнения (к) для приближенного решения задач при выборе функции φi обязательными являются только геометрические граничные условия, а статические граничные условия и дифференциальное уравнение задачи удовлетворяются автоматически.
|
|
|
Таким образом, решение задачи об изгибе пластинки методом Ритца–Тимошенко состоит в следующем. Приближенное значение функции прогибов  (x,y) выбираем в форме двойного ряда:
(x,y) выбираем в форме двойного ряда:
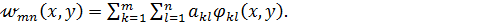 (л)
(л)
Функции 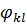 должны удовлетворять геометрическим граничным условиям. Вычисляем приближенное значение потенциальной энергии системы
должны удовлетворять геометрическим граничным условиям. Вычисляем приближенное значение потенциальной энергии системы  . Для определения постоянных
. Для определения постоянных 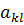 используем систему уравнений (7.2.5), которые в данном случае примут вид
используем систему уравнений (7.2.5), которые в данном случае примут вид
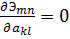
 (7.2..6)
(7.2..6)
Решив эту систему уравнений, найдем параметры 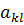 ,которые подставим в функцию прогибов (л) и получим приближенное решение задачи об изгибе пластинки.
,которые подставим в функцию прогибов (л) и получим приближенное решение задачи об изгибе пластинки.
Следует заметить, что, хотя удовлетворение статических граничных условий в методе Ритца–Тимошенко необязательно, лучше по возможности выбирать функции 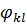 так, чтобы они удовлетворяли всем граничным условиям, как геометрическим, так и статическим. В этом случае ряд быстрее сходится к точному решению, а при вычислениях бывает достаточно ограничиться одним-двумя членами ряда.
так, чтобы они удовлетворяли всем граничным условиям, как геометрическим, так и статическим. В этом случае ряд быстрее сходится к точному решению, а при вычислениях бывает достаточно ограничиться одним-двумя членами ряда.
|
|
|


