 |
Основные принципы разработки и анализа алгоритмов
|
|
|
|
При построении алгоритма для сложной задачи используют системный подход -использованием декомпозиции (нисходящее проектирование сверху-вниз) и синтеза (программирование снизу-вверх). Как и при разработке структуры любой сложной системы, при формировании алгоритма используют дедуктивный и индуктивный методы..
При дедуктивном подходе рассматривается частный случай общеизвестныхалгоритмических моделей. Здесь при заданных предположениях известный алгоритм приспосабливается к условиям решаемой задачи. Например, многие вычислительные задачи линейной алгебры, в частности, нелинейные уравнения, системы алгебраических уравнений и т.п., могут быть решены с использованием известных методов и алгоритмов, для которых существует множество специальных библиотек подпрограмм, модулей. В настоящее время получили распространение специализированные пакеты, позволяющие решать многие задачи (Mathcad, Eureka, Reduce— Autocad и т.п.).
Индуктивный способ предполагает эвристический системный подход (декомпозиция - анализ - синтез). В этом случае общих и наиболее удачных методов не существует. Возможны некоторые подходы, позволяющие в каждом конкретном случае находить и строить алгоритмы. Методы разработки алгоритмов можно разбить на методы частных целей, подъема, отрабатывания назад, ветвей и границ и т.п.
Одним из системных методов разработки алгоритмов является структурное программирование. Принципы структурной алгоритмизации ранее излагались в гл. 1 (п. 1.8). Повторим их более формально с упором на реализацию в практически программировании.
Структурное программирование основано на использовании блок-схем, формируемых с помощью управляющих структурных элементов. Блок-схема - это ориентированная сеть, у которой могут быть вершины типа изображенных на рис. 3.5.
|
|
|
Выделяют три базовых структурных элемента (управляющие структуры): композицию, альтернативу, итерацию.
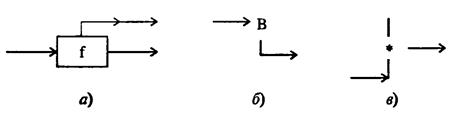
Рис. 3.5. Функциональные (а), предикатные (б) и объединяющие (в) вершины
Композиция - это линейная конструкция алгоритма, составленная из последовательно следующих друг за другом функциональных вершин, рис.3.6.
begin S1;S2; end
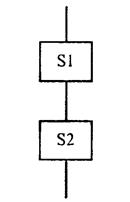
Рис. 3.6. Структура «композиция»
Альтернатива - это конструкция ветвления, имеющая предикатную вершину. Конструкция ветвления в алгоритмах может быть представлена в виде развилки (а), неполной развилки (б) и выбора (в) (рис. 3.7).

Рис. 3. 7. Структура «альтернатива». Здесь В - условие (логическое выражение)
Итерация - это циклическая конструкция алгоритма, которая, вообще говоря, является составной структурой, состоящей из композиции и альтернативы. Итерации могут быть представлены в двух формах: с предусловием (а) и с постусловием (о) (рис.3.8).
Каждая из рассмотренных структур имеет один вход и один выход. Поэтому любая компьютерная программа может быть представлена блок-схемой, сформированной из представленных трех управляющих структур.
Процесс структурного программирования обычно начинается с разработки блок-схемы. Для представления алгоритма в полном и законченном виде, а также
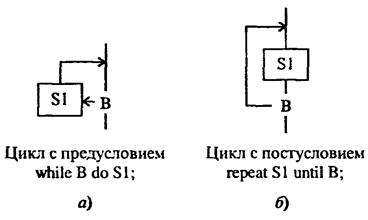
Рис. 3.8. Структура «итерация»
для обозначения связей с окружающей средой добавляют дополнительные структуры ввода-вывода и начала-конца программного блока, модуля, алгоритма:

Заметим, что для начального шага разработки программы чрезвычайно важным и необходимым является определение исходных (ввод) и выходных (вывод) данных задачи. С этого этапа начинается разработка практически любого алгоритма.
Метод разработки программы сверху-вниз предполагает процесс пошагового разбиения алгоритма (блок-схемы) на все более мелкие части до уровня элементарных конструкций, для которых можно составить конкретные команды. Идея структурного программирования сверху-вниз состоит в том, что, если для некоторой функции f существует ее композиция через две другие функции g и h, т.е. f=h(g(х)), то проблема разработки алгоритма для f сводится к проблемам разработки алгоритмов для h и g. В структурном программировании сверху-вниз на каждом шаге пытаются текущую функцию выразить как композицию двух (или более) других функций, которые представимы в виде рассмотренных выше управляющих структур.
|
|
|
Для иллюстрации технологии структурного программирования сверху-вниз рассмотрим два примера - сначала простой, затем существенно более сложный.
Пример 1. Технология разработки программы решения квадратного уравнения.
На рис. 3.9 проиллюстрирована пошаговая детализация процесса построения алгоритма. Заметим, что для начального шага разработки программы имеем в качеств исходных данных коэффициенты а, b, с квадратного уравнения ax2 + bx + с = 0, а на выходе - значения двух корней х 1, х2.
Пример 2. Рассмотрим более сложный и поучительный пример структурной программирования, известный в литературе как «тур шахматного коня». В задаче необходимо ответить на вопрос, существует ли при заданном положении шахматного коня последовательность его ходов, единожды содержащая все клетки шахматного поля.
Попытка быстро ответить на этот вопрос приводит к перебору всех возможн маршрутов коня. Число вариантов перебора чрезвычайно велико, и поиск нужного маршрута лучше поручить компьютеру.
Одной из эвристических стратегий алгоритма может быть следующая. Haчиная с произвольного поля i,j (на рис.3.10 i = 4,j = 4), пытаемся пойти на поле *1, если невозможно, то на поле *2; при неудаче - на поле *3 и т.д.по часовой стрелке
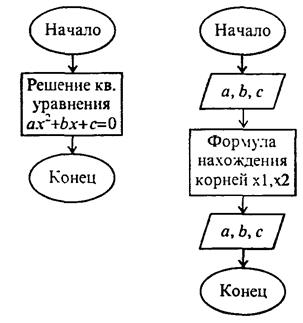
Рис. 3.9. Пошаговая детализация построения алгоритма
(варианты возможных ходов приведены на рисунке справа). Сделав очередной ход на пустую клетку, запишем в нее номер очередного хода и снова осуществляем процедуру поиска нового хода. В случае, когда из очередной клетки невозможно сделать ход, прерываем маршрут и выводим результат в виде таблицы, соответствующей шахматному полю, в которой раставлены ходы коня. Очевидно, что такая стратегия лишь при удаче может дать полный тур коня.
|
|
|
Итак, исходные данные задачи - произвольные начальные координаты коня i,j от 1 до 8. Результат - возможный маршрут коня из заданного поля. Удачным считается маршрут, содержащий все 64 хода, т.е. полный тур коня.
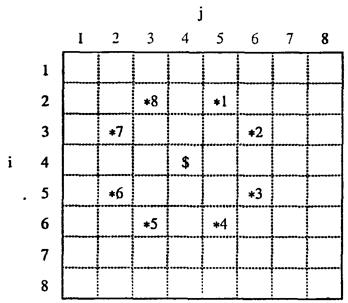
F Рис.3.10. Иллюстрация к задаче «тур шахматного коня»
Инициализация доски предполагает задание двумерного массива размером 8х8 с нулевыми элементами. В дальнейшем элемент a[iJ] принимает значения номера очередного хода. Распечатать результат - означает вывести таблицу а[1..8,1..8].Нарис.3.12 показан один из результатов возможного маршрута коня из начального поля i=l, j=l.

Рис. 3.11. Пошаговая детализация построения алгоритма к примеру 2
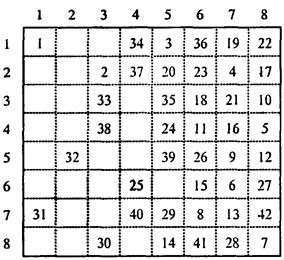
Рис. 3.12. Возможный результат маршрута коня из поля (1.1)
Программа 35
Program Tur_Konja;
var a: array[1..8,1..8] of integer;
im, jm:array(l..8] of integer;
i, j, k, n, inac, jnac: integer;
inext, jnext: integer;
begin (-----инициализация шахматной доски-—--}
for i:=l to 8 do for j:=l to 8 do a[i,j]:=0;
im[l]:=-2; jm[l]:=l.; im[2]:=-1; jm[2]:=2; im[3]:=1; jm[3]:=2;
im[4]:=2; jm[4):=l; im[5]:=2; jm[5]:=-!; im[6]:=1; jm(6]:=-2;
im[7]:=-l; jm[7]:=-2; im[8]:=-2; jm[8]:=-l;
write('введи начальные координаты коня 0<i,j<9: ');
readln(inac,jnac);
a[inac,jnac]:=1; i:=inac; j:=jnac; n:=2; k:=l;
while k<=8 do
begin inext:=i+im(k]; jnext:=j+jm (k];
if (inext<l) or (inext>8) or (jnext<l) or
(jnext>8) or (a[inext,jnext]<>0)
then k:=k+l
else begin a(inext,jnext]:=n; n^n+l; i:«-inext;
j:«jnext; k:=l;
end;
end;
{--------вывод результата прохода—————)
for i:=l to 8 do
begin writeln; writeln; for j:=l to 8 do write(a(i,j]:2,' ')
end;
writeln; write('кол-во шагов = ',n-l); readln;
end.
Зачастую используют альтернативный процедуре сверху-вниз метод структурного программирования сннзу-вверх. По сути мы приходим к конечному результату системным методом. Сначала разбиваем задачу на отдельные блоки (модули) с их связями между собой (декомпозиция), затем, после их разработки, проводим сборку блоков в единую программу (синтез). Принцип снизу-вверх широко распространен среди программистов, которые предпочитают модульный подход, предполагающий максимальное использование стандартных и специализированных библиотек процедур, функций, модулей и объектов.
|
|
|
Задания
1. Используя принцип проектирования сверху-вниз постройте блок-схему и программ) для решения системы линейных алгебраических уравнений методом Гаусса.
2. Разработайте алгоритм и программу поиска тура коня по другой стратегии, например, по случайному выбору очередного хода из числа возможных.
4.3. МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ,
ОРИЕНТИРОВАННЫЕ НА СТРУКТУРЫ ДАННЫХ
Часто на технологию разработки алгоритма влияют структуры данных, используемых в программе. Удачный выбор структур данных позволяет зачастую легко строить эффективные алгоритмы. Методы программирования, в которых такое влияние доминирует, называют методами, ориентированными на структуры данных. Рассмотрим некоторые классы задач, где полезны такие структуры как связные списки, очереди, стеки, деревья.
Сортировка массивов данных, т.е. расположение их элементов в определенном порядке, являясь одной из важнейших прикладных задач при эксплуатации информационных систем, требует больших временных затрат и ресурсов памяти ЭВМ. Легко представить возникающие трудности, когда в массиве данных происходят удаления и внесения новых записей. Обычные подходы заставят нас осуществлять заново сортировку измененного массива с физическими перестановками записей согласно известным процедурам упорядочивания.
Попробуем проблему решить с помощью линейного связанного списка. Массив преобразуют в двумерный, в котором по второму индексу (целые неотрицательные числа, называемые связями или указателями) располагают номера элементов массива.
| Info | Link | |
| 1 Петров 2 Смирнов 3 Алексеев | Линейный связанный список - это конечный набор пар, состоящих из информационной части (Info) и указующей части (Link). | |
| N Кузнецов |
Линейные связанные списки являются эффективной структурой данных для моделирования ситуаций, в которых подвергаются изменениям упорядоченные массивы элементов данных. Особенно важно их использование при процедурах внесения или удаления элементов из середины массива. Когда модификации касаются лишь начала или/и конца, то необходимость в связанных списках отпадает, и становится достаточным использование одномерного исходного массива. Здесьнапомощь приходят стеки и очереди.
Пусть, например, задано арифметическое выражение. Требуется определить, правильно ли расставлены в выражении скобки.
Для решения подобных задач используют стековую память (называемую просто «стек»). Стек представляет последовательность данных и имеет лишь одну границу для добавления и удаления элементов. В нашем случае в стек помещаются и удаляются скобки.
|
|
|
Первым необходимым условием правильности расстановок скобок является совпадение количества левых и правых скобок. Такой контроль легко осуществить введя счетчик top, который при просмотре выражения и обнаружении левой скобки (допустим, что имеем только круглые скобки '(') увеличивается на +1. Если на очередном месте встретилась правая скобка, то значение счетчика уменьшается на 1. Тогда правильность расстановки определяется по итоговому значению top.
Программа 36
program skobkal; (*проверка скобок по количеству*)
var top, i, n: integer; slovo: string[100]; skob: string[100];
begin
write('введи арифметическое выражение: ');
readln(slovo); n:length(slovo);
top:=0; skob:=''; i:=l;
while (i<=n) do begin
if slovo[i]=')' then begin top:=top+1; skob:=skob+slovo[i] end;
if slovo[i]=')' then begin
top:=top-l; skob:=skob+slovo[i] end;
i:=i+l
end;
writeln(skob);
if top=0 then write('выражение правильное') i else write('выражение неправильное');
readln.
end.
Строковая переменная skob предназначена "для визуализации всех имеющихся скобок в выражении.
В случае, когда в выражении используются фигурные, квадратные и круглые скобки, задача усложняется тем, что необходим еще контроль соответствия левых и правых скобок. В этой связи удобно использовать стек, в котором помещаются очередные левые скобки. При обнаружении правой скобки из вершины стека извлекается левая скобка, помещенная последней, и проводитсяих идентификация. Полный текст программы представлен ниже.
Программа 37
program skobka2; (*проверка расстановок скобок*) var top, i, n: integer;
slovo: string[100];
store: array [1.. 100] of char; -x: char.; sicob: string[100];
p: boolean;
begin
write('введи арифметическое выражение: ');
readln(slovo); n:=length(slovo);
top:=0; p:=true; skob:=''; i:=1;
while (i<=n)and(p) do
begin if (slovo[i]='(') or (slovo[i]='[') or (slovo[i]='(') then begin top:=top+l; store[top]:=slovo[i];
skob:=skob+slovo[i] end;
if slovo(i]='}' then begin x:=store(top];
if x<>'(' then p:=false
else begin top:=top-l; skob:=skob+slovo{i] end;
end;
if slovo[i]=']' then begin x:=store[top];
if x<>'[' then p:=false
else begin top:=top-l; skob:=skob+slovo[i] end;
end;
if slovo(i]=')' then begin x:=store(top];
if x<>'(' then p:=false
else begin top:=top-l; skob:=skob+slovo[i] end;
end;
i:=i+l end;
writeln(skob); if top=0 then write('выражение правильное') else write('выражение неправильное');
readln
end.
Структура данных «очередь» используется для моделирования систем массового оослужнвания: очереди людей в магазинах, транспортных потоков, производственных линий и т.п. Рассмотрим модельную ситуацию с формированием очереди в ком-нибудь учреждении сферы обслуживания, например, в банке.
Пусть задана скорость поступления клиентов в банк и известна скорость обслуживания. Вместо скорости поступления клиентов будем задавать вероятность р их появления в единицу времени. За скорость обслуживания примем число v, соответствующее времени обслуживания одного клиента. Для простоты примем в качестве массива данных о клиентах банка числовой массив со случайными числами из интервала 1..100. Для формирования очереди достаточно ввести две переменные, которые указывают на начало и конец списка данных.
Следующая программа демонстрирует динамику обслуживания очереди.
Программа 38
program bank;
uses crt;
type item = integer;
var qq:array[l..100] of item; i, t, v, L, R; integer;
р, x: real; st: string[10];
begin (*начальное состояние очереди*)
qq[l]:=random(100); qq[2]:=random(100); qq[3]:=random(100);
L:=l; R:=3; р:0,6 v:=2; randomize; t:=0;
repeat
t:=t+l; x:=random; if x<p then begin R:=R+1;
qq[R]:=random(100);
end;
if (t mod v=0) then L:=L+1;
until keypressed or (R>100);
(*вывод состояния очереди на момент прерывания*) for i:=L to R do writeln(qq(i]);
readin;
end.
Контрольные задания
1. Постройте программу упорядочивания списка фамилий студентов группы с использованием линейного списка.
2. С помощью стека организуйте алгоритм, который определяет, является ли заданное слово палиндромом («перевертышем»).
3. Придумайте задачу на использование очереди.
РЕКУРСИВНЫЕ АЛГОРИТМЫ
Изучая в предыдыщем разделе язык Паскаль, мы уже использовали понятие рекурсии. Однако, оно столь важно и принципиально, что с ним следует познакомиться детальнее.
Рекурсией называют метод определения или вычисления функции, процедуры или решения задачи посредством тон же функции, процедуры и т.д. Рекурсивные алгоритмы широко используют методы частных целей, подъема и отрабатывания назад. На эвристическом уровне рекурсия позволяет эффективно использовать метод проб и ошибок.
Продолжим рассмотрение примера задачи тура шахматного коня из предыдущего раздела. Приведенный там алгоритм строил возможный путь коня по простой стратегии очередного хода на свободное место по принципу часовой стрелки. Однако, он не позволял гарантированно найти полный тур коня. Применим простую эвристическую модель решения задачи - в случае отсутствия возможности очередного хода осуществляется возврат коня на предыдущее поле и возобновление поиска дальнейшего маршрута по другому пути. Подобный процесс называют возвратом (или откатом). Его можно осуществлять по универсальной схеме:
procedure RETR;
begin
инициализация начального хода repeat выбор очередного хода
if подходит then его запись;
if решение не полное then RETR;
if неудача then стирание хода и возвратна предыдущий until удача or нет хода
end.
Подобная рекурсивная процедура и уже известный алгоритм, рассмотренный выше, позволяют построить нужную программу. Ниже представлена программа тура коня для произвольного поля NxN, позоляющая отыскивать полный тур с любого начального положения. Для наглядной иллюстрации процесса поиска в глубину и в ширину с возвратами в программе в комментарные скобки обозначены команды вывода промежуточных результатов.
Программа 39
program tur;
var i, j, ii, jj, n, nn: integer; q: boolean;
dx, dy:array[1..8] of integer; h:array[1..8,1..8] of integer;
(*рекурсивная процедура - попытка сделать ход*)
procedure try(i,x,у:integer; var q:boolean);
var k, u, v: integer; ql: boolean;
begin
k:=0; repeat k:=k+l; ql:=false; u:=x+dx[k]; v:=y+dy(k];
if ((1<=u) and(u<=n) and (1<=v) and (v<=n)) and(h[u,v]=0)
then begin h[u,v]:=i;
(*для отладки и наблюдения процесса поиска с возвратом*')
for ii:=l to n do begin for jj:= 1 to n do
write(h[ii,jj]:5); writeln;
end;
readin;
if i<nn then begin try(i+l,u,v,ql);
if not(ql) then h[u,v]:=0
else ql:=truer;
end
else ql:=true
end;
until (ql) or (k=8);
q:=ql
end; (* конец процедуры*)
begin
dx[l] =2: dx[2]:=l; dx[3]:=-l; dx[4]:=-2; dx[5]:=-2;
dx[6] =-1: dx[7]:=l; dx[8]:=2; dy[l]:=l; dy[2]:=2;
dy[3] =2: dy[4]:=l; dy[5]:=-l; dy[6]:=-2;
dy[7] =-2: dy[8]:=-1;
write ('введи n: '); readln(n);
for i =1 to n do for j:=1 to n do h[i,j] :=0;
write; ('введи i,j: '); readln(i,j); nn:=n*n;
h[i,j]:=l; try(2,i,j,q);
if q then begin
for i:=l to n do begin
for j:= 1 to n do write(h[i,j]:5);
writeln;
end;
end ' else writeln('нет маршрута');
readln
end.
Для n = 5 и n = 6 алгоритм быстро находит искомые туры коня. Для n = 8 время решения может возрасти в несколько десятков раз.
Рассмотрим еще два замечательных рекурсивных алгоритма, позволяющих строить регулярные образы, в конечном счете образующие красивые узоры на экране дисплея. Узор образуется из серии выстраиваемого определенным образом заданного мотива. '
Ниже представлена программа, использующая при построении узора кривые Серпинского, рис. 3.13.

Рис. 3.13. Примеры кривых Серпинского
На рисунке изображены кривые Серпинского S1 и S2 первого и второго порядков. Кривую Серпинского Si можно разбить на 4 части: Ai, Bi, Ci, Di, которые соединяются четырьмя отрезками Эти четыре части кривой представляют одну и ту же ломаную, поворачивающуюся каждый раз на 90 градусов. Нетрудно увидеть рекурсивные схемы, по которым ломаные Ai, Bi. Ci, Di получаются из кривых A(i-l). B(i-l), C(i-l), D(i-l), размеры которых при этом сокращаются вдвое:
| Ai: A(i-l) Bi: B(i-l) Ci: C(i-l) Di: D(i-l) | B(i-l) – C(i-l) | D(i-l) – A(i-l) | | D(i-l) A(i-l) B(i-l) C(i-l) | A(i-l) B(i-l) C(i-l) D(i-l) |
Векторы, соединяющие отдельные элементы кривых, образуют с осью абсцисс углы, кратные pi/4; средние векторы во всех схемах имеют длину, в два раза большую, чем крайние. Для построения вектора длины U под углом T*pi/4 к оси абсцисс в программе описана процедура linep(T,U:integer):
Программа 40
program serpinsk;
uses crt,graph;
const sq=512;
var i, xO, yO, x, y, t, u, gd, gm: integer; ch:chart;
procedure linep(t,u:integer);
var xl, yl:integer;
begin x:=x+round(u*cos(t*pi/4));
y:=y-round(u*sin(t*pi/4)); lineto(x,y);
end;
procedure b(i:integer); forward;
procedure с(i:integer); forward;
procedure d(i:integer); forward;
procedure a(i:integer);
begin
if i>0 then begin a(i-l); linep(7,u); b(i-l); linep(0,2*u);
d(i-l); linep(l,u); a(i-l)
end end; •
procedure b;
begin
if i>0 then begin b(i-l); linep(5,u); c(i-l); linep(6,2*u);
a(i-l); linep(7,u); b(i-l)
end end;
procedure c;
begin
if i>0 then begin c(i-l); linep(3,u); d(i-l); linep(4,2*u);
b(i-l); linep(5,u);C(i-l)
end end;
procedure d;
begin
if i>0 then begin d(i-l); linep(l,u); a(i-l); linep(2,2*u);
c(i-l); linep(3,u); d(i-l) end. end;
begin gd:=0; initgraph(gd, gm, ' ');
u:=sq div 4; x0:=320; y0:=128; i:=0;
repeat
i:=i+l; x0:=x0-u; u:=u div 2; y0:=y0-u;
x:=x0; y:=y0; setcolor(2*i);
moveto(x,y); a(i); linep(7,u); b(i);
linep(5,u); c(i); linep(3,u);
d(i); linep(l,u); delay(2000) until i=5;
settextstyle(0,0,1);
outtextxy(200, 470, 'КРИВЫЕ СЕРПИНСКОГО S1 - S5');
readln; closegraph
end.
В 1891 г. Д. Гильберт открыл серию рекурсивных кривых, которые получили название кривых Гильберта. Кривая Гильберта Hi, подобно кривым Серпинского, может быть получена из четырех экземпляров кривой H(i-l) вдвое меньшего размера, повернутых должным образом и соединенных отрезками. Ниже приводится программа, рисующая узор из шести кривых Гильберта.
Программа 41
program hilbert;
uses crt,graph;
const sq=448;
var i,x0,y0,x,y,t,u,gd,gm:integer; ch:char;
procedure linep(t,u:integer);
var xl,yl:integer;
begin x:=x+round(u*cos(t*pi/4)); y:=y-round(u*sin(t*pi/4));
lineto (x,y);
end;
procedure b(i:integer); forward;
procedure с(i:integer); forward;
procedure d(i:integer); forward;
procedure a(i:integer);
begin
if i>0 then begin d(i-l); linep(4,u); a(i-l); linep(6,u);
a(i-l); linep(0,u); b(i-l)
end end;
procedure b;
begin
if i>0 then begin c(i-l); linep(2,u); b(i-l); linep(0,u);
b(i-l); linep(6,u); a(i-l)
end end;
procedure c;
begin
if i>0 then begin b(i-l); linep(0,u); c(i-l); linep(2,u);
c(i-l); linep(4,u); d(i-l)
end end;
procedure d;
begin
if i>0 then begin a(i-l); linep(6,u); d(i-l); linep(4,u);
d(i-l); linep(2,u); c(i-l)
end end;
begin gd:=0; initgraph(gd, gm, ' '); x0:=320; y0:=240; u:=sq; i:=0;
repeat
i:=i+l; u:=u div 2;
x0:=x0+(u div 2); y0:=y0-(u div 2);
x:=x0; y:=y0; setcolor(2*i);
moveto(x,y); a(i); delay(2000) until i=6;
settextstyle(0,0,1);
outtextxy(220,470, 'КРИВЫЕ ГИЛЬБЕРТА HI - Н6');
readin; closegraph
end.
Контрольные задания
1. Разработайте алгоритм и программу расстановки ферзей на шахматном поле таким образом, чтобы ни один из них не бил другого,
2. Разработайте программу игры «Ханойские башни».
3. Предложите другие модификации алгоритма полного тураконя.
4.5. ВАЖНЕЙШИЕ НЕВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ
(ПОИСК И СОРТИРОВКА)
Одними из важнейших процедур обработки структурированной информации являются сортировка и поиск. Сортировкой называют процесс перегруппировки заданной последовательности (кортежа) объектов в некотором определенном порядке. Определенный порядок (например, упорядочение в алфавитном порядке, по возрастанию или убыванию количественных характеристик, по классам, типам и т.п) в последовательности объектов необходим для удобства работы с этими объектами. В частности, одной из целей сортировки является облегчение последующего поиска элементов в отсортированном множестве. Под поиском подразумевается процесс нахождения в заданном множестве объекта, обладающего свойствами или качествами задаваемого априори эталона (или шаблона).
Очевидно, что с отсортированными (упорядоченными) данными работать намного легче, чем с произвольно расположенными. Упорядоченные данные позволяют эффективно их обновлять, исключать, искать нужный элемент и т.п. Достаточно представить, например, словари, справочники, списки кадров в неотсортированном виде и сразу становится ясным, что поиск нужной информации является труднейшим делом, если не невозможным.
Существуют различные алгоритмы сортировки данных. И понятно, что не существует универсального, наилучшего во всех отношениях алгоритма сортировки. Эффективность алгоритма зависит от множества факторов, среди которых можно выделить основные:
• числа сортируемых элементов;
• степени начальной отсортированности (диапазона и распределения значений сортируемых элементов);
• необходимости исключения или добавления элементов;
• доступа к сортируемым элементам (прямого или последовательного).
Принципиальным для выбора метода сортировки является последний фактор. Если данные могут быть расположены в оперативной памяти, то к любому элементу возможен прямой доступ. Удобной структурой данных в этом случае выступает массив сортируемых элементов. Если данные размещены на внешнем носителе, то к ним можно обращаться лишь последовательно. В качестве структуры подобных данных можно взять файловый тип.
В этой связи выделяют сортировку двух классов объектов: массивов (внутреняя сортировка) и файлов (внешняя сортировка).
Процедура сортировки предполагает, что при наличии некоторой упорядочивающей функции F расположение элементов исходного множества меняется таким образом, что
a1, а2… аn → ak1, ak2…akn
F(ak1) < F(ak2) < F(akn)
где знак неравенства понимается в смысле того порядка, который установлен в сортируемом множестве.
Поиск и сортировка являются классическими задачами теории обработки данных, решают эти задачи с помощью множества различных алгоритмов. Рассмотрим наиболее популярные из них.
Поиск. Для определенности примем, что множество, в котором осуществляется поиск, задано как массив
var a:array[0..N] of item;
где item - заданный структурированный тип данных обладающий хотя бы одним полем (ключом), по которому необходимо проводить поиск.
Результатом поиска, как правило, служит элемент массива, равный эталону, или отсутствие такового.
Линейный поиск. Процедура заключается в простом последовательном просмотре всех элементов массива и сравнении их с эталоном X.
i:=0;
while (i<=N)and(a[i]<>X) do i:=i+1 end.
Часто бывает целесообразнее осуществлять поиск с барьером, вводя дополнительно граничный элемент массива a[N+l]:
a[N+l]:=X;i:=0;
while a[i]<>X do i:=i+l end.
Равенство i = N + 1 означает, что совпадений не было, т.е. что эталонный элемент отсутствует.
Попытайтесь разобраться в чем различие представленных конструкций. Приведем пример программы поиска эталона х в массиве а[0..n].
Программа 42
program poiskl; (*линейный поиск*) const N=8;
type item= integer;
var a: array[0..n] of item; i:integer; x: item;
begin
(*задание искомого массива*) for i:=0 to N do
begin writet'Bвeди элемент a[ ',i, ']= '); readln(a[i]);
end;
writeln; write('введи эталон x= '); readln(x);
(* линейный поиск*)
i:=0; while (i<=N)and(a[i]<>X) do begin i:=i+l end;
(*вывод результата*)
if i<=N then write('найден элемент на ',i, ' месте ') else write('такого элемента в массиве нет ');
readin
end.
Поиск делением пополам. В большинстве случаев процедура поиска применяется к упорядоченным данным (телефонный справочник, библиотечные каталоги и пр.). В подобных ситуациях эффективным алгоритмом является поиск делением пополам. В этом методе сравнение эталона Х осуществляется с элементом, расположенным в середине массива и в зависимости от результата сравнения (больше или меньше) дальнейший поиск проводится в левой или в правой половине массива.
L:=0; R:=N; while L<R do
begin
m:=(L+R) div 2;
if a[m]<X then L:=m+l else R:=m;
end;.
Например, пусть эталонный ключ х=13, а в массиве имеются следующие элементы:
а[0]=1; а[1]=3; а[2]=4; а[3]=7; а[4]=8; а[5]=9; а[6]=13; а[7]=20; а[8]=23.
Бинарный процесс поиска показан ниже:
1 3 4 7 8 9 13 20 23 - элементы массива
0 1 2 3 4 5 6 7 8- порядковые номера элементов
L m R
L m R
a[m]=x =>поиск закончен и m = 6
Программа поиска представлена ниже.
Программа 43
program poisk2; (*поиск делением пополам*)
const N=8;
type item= integer;
var a: array[0..n] of item; i, L, R, m:integer; x: item; f:
boolean;
begin
(*задание искомого массива*)
for i:=0 to N do
begin write('введи элемент a[',i, '1= '); readln(a[i])
end;
writeln; write('введи эталон х= '); readln(x);
(*бинарный поиск*)
L:=0; R:=N; f:=false;
repeat m:=(L+R) div 2; if a[m]=X then f:=true;
if a[m]<X then L:=m+l
else R:=m;
writeln(m,L,R);
until (L>=R)or(f);
(*вывод результата*)
if f then write('найден элемент на ',m, ' месте') else write('такого элемента в массиве нет ');
readln
end.
Сортировка массивов. Как и в случае поиска определим массив данных:
var a: array [0.. N] of item
Важным условием сортировки массива большого объема является экономное использование доступной памяти. В прямых методах сортировки осуществляется принцип перестановки элементов «на том же месте». Ниже рассмотрим три группы сортировок: с помощью включения, выбора и обмена.
Сортировка с помощью включения Кто играл в карты, процедуру сортировки включениями осуществлял многократно. Как правило, после раздачи карт игрок, держа карты веером в руке, переставляет карты с места на место стремясь их расположить по мастям и рангам, например, сначала все тузы, затем короли, дамы и т.д. Элементы (карты) мысленно делятся на уже «готовую последовательность» и неправильно расположенную последовательность. Теперь на каждом шаге, начиная с i = 2, из неправильно расположенной последовательности извлекается очередной элемент и перекладывается в готовую последовательность на нужное место.
for i:=2 to N do begin
x:=a[i];
<включение х на соответствующее место готовой последовательности a[l],...,a[i]>
end
Поиск подходящего места можно осуществить одним из методов поиска в массиве, описанным выше. Затем х либо вставляется на свободное место, либо сдвигает вправо на один индекс всю левую сторону. Схематично представим алгоритм для конкретного примера:
| Исходные элементы | |||||
| i=2 | |||||
| i=3 | |||||
| i=4 | |||||
| i=5 |
В алгоритме поиск подходящего места осуществляется как бы просеиванием х при движении по последовательности и сравнении с очередным a[j]. Затем х либо вставляется на свободное место, либо a[j] сдвигается вправо и процесс как бы «уходит» влево.
Программа 44
program sortirov)ca_l;
(*сортировка включением по линейному поиску*) const N=5;
type item= integer;
var a: array[l..n] of item; i, j: integer; х: item;
begin (*задание искомого массива*)
for i:=l to N do begin write('введи элемент a[',i,']=');
readln(a[i]) end;
for i:=l to N do begin write(a[i], ' ');
end;
writeln;
(*алгоритм сортировки включением*).for i:=2 to n do begin
x:=a[i]; j:=i; a[0]:=x; (*барьер*)
while x<a[j-l] do
begin
a[j]:=a[j-l); j:=j-l;
end;
a[j]:=x;.
(for k:=l to n do write(a[k.l, ' ') end; writeln;) end;
(*вывод отсортированного массива*) for i:=l to N do begin.
write(a[i], ' ');
end;
readln;
end.
В рассмотренном примере программы для анализа процедуры пошаговой сортировки можно рекомендовать использовать трассировку каждого прохода по массиву с целью визуализации его текущего состояния. В тексте программы в блоке непосредственного алгоритма сортировки в фигурных скобках находится строка, которая при удалении скобок выполнит требуемое (параметр k необходимо описать в разделе переменных - var k:integer). Во всех последующих программах сортировки легко осуществить подобную процедуру.
Вернемся к анализу метода прямого включения. Поскольку готовая последовательность уже упорядочена, то алгоритм улучшается при использовании алгоритма поиска делением пополам. Такой способ сортировки называют методом двоичного включения.
Программа 45
program sortirovka_2;
(*сортировка двоичным включением*) const N=5;
type item= integer;
var a: array(l..n] of item; i, j, m, L, R: integer; x: item;
begin
(*задание элементов массива*) for i:=l to N do
begin write('Bведи элемент a[',i,']= '-); readln(a[i]);
end;
for i:=l to N do
begin write (a[i], ' ');
end;
writeln;
(*алгоритм сортировки двоичным включением*)
for i:=2 to n do begin
x:=a(i]; L:=l; R:=i;
while L<R do begin
m:=(L+R) div 2; if a[m]<=x then L:=m+l else R:=m;
end;
for j:=i downto R+l do a(j] :=a [j-1];
a[R]:-x;
end;
(* вывод отсортированного массива*)
for i:=l to N do
begin write(a[i], ' ');
end;, readln;
end.
Одиниз вариантов улучшенной сортировки включением был предложен Д.Шеллом. Его метод предполагает сначала отдельную группировку и сортировку элементов, отстоящих друг от друга на некотором расстоянии, например 4 (четвертная сортировка), после первого прохода перегруппировку элементов таким образом, чтобы каждый элемент группы отстоял от другого на 2 номера, после двойной сортировки на третьем проходе одинарную (обычную) сортировку.
| Исходные элементы | ||||||||
| Четвертная сортировка | ||||||||
| Двойная сортировка | ||||||||
| Одинарная сортировка |
Каждая из сортировок основывается на алгоритме прямого включения и, соответственно,должна программироваться аналогично. Если для условия окончания поиска использовать барьер, а их необходимо ставить для каждой из сортировок, то необходимо расширить границы массива на несколько компонентов (барьеров) влево, т.е. использовать массив а[-r..n], где r - количество сортировок.
Сортировка с помощью прямого выбора. Алгоритм прямого выбора является одним из распространенных в силу своей простоты. Сначала определяют минимальный элемент среди всех элементов массива, затем его меняют местами с первым. Далее процесс повторяется с той лишь разницей, что минимальный ищется со второго и меняется со вторым и т.д.
| i=2, min= 11 | |||||
| i=3.min=12 | |||||
| i=4, min=13 | |||||
| i=5,min=15. |
Программа 46
program sortirovka_3;
(*улучшенная сортировка включением - сортировка Шелла*)
const N=8; t=4;
type item= integer;
var a: array[-9..n] of item; i, j, k, s:integer; x: item;
m: l..t; h:array [l..t] of integer;
begin
(*задание искомого массива*)
for i:=l to N do
begin write('введи элемент a[',i, ']=') readln(a[i])
end;
for i:=l to N do begin write(a[i], ' ');
end;
writeln;
(*алгоритм Шелла*)
h[l]:=9; h[2]:=5; h[3]:=3; h[4]:=1;
for m:=l to t do
begin k:=h[m]; s:=-k; (*барьеры для каждого шага*)
for i:=k+l to n do
begin x:=a[i], j:=i—k; if s=0 then s:=-k;- s:=s+l;
a[s]:=x; while x<a[j] do begin a[j+k]:=a(j]; j:=j-k;
end;
a[j+k]:=x
end;
end;
(*вывод отсортированного массива*)
for i:=l to N do begin write(a[i], ' ');
end;
readln;
end.
Программа 47
program sortirovka 4;
(*сортировка прямым выбором*)
const N=5;
type item= integer;
var a: array[l..n] of item; i, j, k: integer; x: item;
begin
(*задание искомого массива*)
for i: =1 to N do
begin write('введи элемент a[', i, ']='); readln(a[i]);
end;
for i:=l to N do begin write(a[i],' ');
end;
writeln;
(*алгоритм прямого выбора*)
for i:=l to n-1 do
begin k:=i; x:=a[i]; (*поиск наименьшего элемента*)
for j:=i+l to n do (*и его индекса из a[i]...a{n]*)
if a[j]<x then begin k:=j; x:=a[k)
end;
a(k]:=a[i]; a[i]:=x;
end;
(*вывод отсортированного массива*)
for i:=l to N do begin write(a[i], ' ');
end;
readln;
end.
Улучшенный метод сортировки выбором с помощью дерева. Метод сортировки прямым выбором основан на поисках наименьшего элемента среди неготовой последовательности. Усилить метод можно запоминанием информации при сравнении пар элементов. Этого добиваются определением в каждой паре меньшего элемента за n/2 сравнений. Далее n/4 сравнений позволит выбрать меньший из пары уже выбранных меньших и т.д. Получается двоичное дерево сравнений после n-1 сравнений у которого в корневой вершине находится наименьший элемент, а любая вершина содержит меньший элемент из двух приходящих к ней вершин. Одним из алгоритмов, использующих структуру дерева, является сортировка с помощью пирамиды (Дж.Вилльямс). Пирамида определяется как последовательность ключей hL...hR, такая, что *
hi<=h2i и hi<=h2i+l, для i=L,...,R/2.
Другими словами пирамиду можно определить как двоичное дерево заданной высоты h, об
|
|
|


