Случаи приведение плоской системы сил к данной точке.

Описанный метод приведения одной силы к данной точке можно применить к какому угодно числу сил. Допустим, что в точках тела А, В, С и D (рис. 30) приложены силы F1,F2,F3,F4. Требуется привести эти силы к точке О плоскости. Приведем сначала силу F1, приложенную в точке А. Приложим в точке О две силы F1' и F1'', параллельные ей и направленные в противоположные стороны. В результате приведения силы F1 получим силу F1', приложенную в точке О, и пару сил F1' F1'' с плечом a1. Поступив таким же образом с силой F2, приложенной в точке В, получим силу F2', приложенную в точке О, и пару сил с плечом a2 т. д. Плоскую систему сил, приложенных в точках А, В, С и D, мы заменили сходящимися силами F1,F2,F3,F4, приложенными в точке О, и парами сил с моментами, равными моментам заданных сил относительно точки О:
Сходящиеся в точке силы можно заменить одной силой F'гл, равной геометрической сумме составляющих,
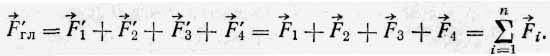Эту силу, равную геометрической сумме заданных сил, называют главным вектором системы сил и обозначают F'гл.

На основании правила сложения пар сил их можно заменить результирующей парой, момент которой равен алгебраической сумме моментов заданных сил относительно точки О и называется главным моментом относительно точки приведения
Следовательно, в общем случае плоская система сил в результате приведения к данной точке О заменяется эквивалентной ей системой, состоящей из одной силы (главного вектора) и одной пары (главного момента). Необходимо усвоить, что главный вектор F'гл является равнодействующей данной системы сил, так как эта система не эквивалентна одной силе F'гл. Только в частном случае, когда главный момент обращается в нуль, главный вектор будет равнодействующей данной системы сил. Так как главный вектор равен геометрической сумме сил заданной системы, то ни модуль, ни направление его не зависят от выбора центра приведения. Значение и знак главного момента Mгл зависят от положения центра приведения, так как плечи составляющих пар зависят от взаимного положения сил и точки (центра), относительно которой берутся моменты.

Могут встретиться следующие случаи приведения системы сил:
1. — общий случай; система приводится главному вектору и к главному моменту.
2. ; система приводится к одной равнодействующей, равной главному вектору системы.
3. ; система приводится к паре сил, момент которой равен главному моменту.
4. ; система находится в равновесии, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы ее главный вектор и главный момент одновременно были равны нулю.

Можно доказать, что в общем случае, когда, всегда есть точка, относительно которой главный момент сил равен нулю.

Рассмотрим плоскую систему сил, которая приведена к точке О, т. е. заменена главным вектором , приложенным в точке О, и главным моментом . Для определенности примем, что главный момент направлен по часовой стрелке, т. е. . Изобразим этот главный момент парой сил FF", модуль которых выберем равным модулю главного вектора, т. е. . Одну из сил, составляющих пару, приложим в центре приведения О, другую силу в точке С, положение которой определится из условия: . Следовательно .

Расположим пару сил так, чтобы сила F'' была направлена в сторону, противоположную главному вектору F'гл. В точке О имеем две равные взаимнопротивоположные силы F'гл и F'', направленные по одной прямой; их можно отбросить (согласно третьей аксиоме). Следовательно, относительно точки С главный момент рассматриваемой системы сил равен нулю, и система приводится к равнодействующей . Теорема о моменте равнодействующей(теорема Вариньона) В общем случае произвольная плоская система сил приводится к главному вектору F'гл и к главному моменту Mгл относительно выбранного центра приведения, причем главный момент равен алгебраической сумме моментов заданных сил относительно точки О: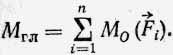

Было показано, что можно выбрать центр приведения, относительно которого главный момент системы будет равен нулю, и система сил приведется к одной равнодействующей , равной по модулю главному вектору 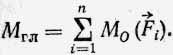. Определим момент равнодействующей относительно точки О. Учитывая, что плечо ОС силы F равно , получаем .

Две величины, порознь равные третьей, равны между собой, поэтому из предыдущих уравнений находим.

Полученное уравнение выражает теорему Вариньона: момент равнодействующей плоской системы сил относительно произвольно взятой точки равен алгебраической сумме моментов составляющих сил относительно той же точки.

Из теоремы Вариньона следует, что главный момент плоской системы сил относительно любой точки, лежащей на линии действия ее равнодействующей, равен нулю.

17. Статический момент площади сечения Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей.

Рассмотрим изменение статических моментов при параллельном переносе осей (рис. 1.1). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты S_x1, S_y1 относительно новых осей x₁, y₁.

Рис. 1.1

Учитывая соотношения x₁ = x - a и y₁ = y - b получим: или S_x1 = Sx - bF; S_y1 = Sy - aF; (1.1) Оси x₁, y₁ можно выбрать таким образом, чтобы выполнились условия: S_x1 = 0, S_y1 = 0. Оси, относительно которых статические моменты сечения равны нулю, называются центральнми. Точка пересечения центральных осей называется центром тяжести сечения. Принимая S_x1 = 0 и S_y1 = 0, из выражения (1.1) координаты центра площади сечения относительно вспомогательных осей x, y определяются по формулам (обозначим x_c = a, y_c = b):

(1.2)

Соответственно, если площадь F и положение центра площади сечения (координаты x_c, y_c) в системе координат 0xy известны, то статические моменты сечения относительно осей x, y можно определить из выражений (1.2): Sx = F y_c; Sy = F x_c. (1.3) Можно показать, что статический момент относительно любой оси, проходящей через центр площади сечения, равен нулю. При определении центра площади сложного сечения применяется следующая процедура: 1) сечение разбивается на n частей, площади (F_i) и положение центров (C_i) площади которых известны; 2) задается вспомогательная система координат, в которой определяются координаты центров площадей (x_ci, y_ci) этих частей; 3) вычисляются координаты составного сечения по формулам: