 |
Колебания математического маятника
|
|
|
|
Колебательное движение - одно из самых распространенных в природе. Разнообразные маятники в часах и других технических устройствах, колебания мембран и оболочек, колебания атомов в молекулах, ионов и молекул в кристаллах и многие другие процессы в живой и неживой природе в чем-то схожи: объект движется таким образом, что многократно проходит через одни и те же точки, периодически воспроизводя одно и то же состояние. Изучив его движение на сравнительно коротком отрезке времени, включающем один период, мы можем составить полное представление о его движении в будущем (если оно не будет изменено вмешательством извне).
Хотя колебательные движения бывают весьма многообразны, их сущность можно постичь на нескольких относительно простых примерах. Остановимся на одном из самых простых, название которого вынесено в заголовок. Этот пример рассматривается в любом школьном курсе физики, но, располагая более совершенным математическим аппаратом и прибегая к компьютерному моделированию, можно продвинуться в изучении колебаний математического маятника дальше и понять закономерности колебательного движения глубже.
Рассмотрим идеализированную систему, состоящую из тела массы т, прикрепленного к нижнему концу жесткого «невесомого» стержня длиной l, верхний конец которого вращается без трения в точке подвеса, рис. 7.17.
Если груз отклонить от положения равновесия на угол θ0 и отпустить, то «математический маятник» будет колебаться в вертикальной плоскости.
Рис.7.17. Колебания математического маятника
Поскольку движение груза происходит по дуге окружности радиуса l, то его положение характеризуется в каждое мгновение углом θ. Линейная скорость и ускорение равны
|
|
|
(7.27)
На груз действуют две силы: сила тяжести 
и упругая сила натяжения стержня 
. При выводе уравнения движения достаточно учесть лишь компоненту силы , направленную по касательной к дуге: F = mg sin θ, направлена она в сторону уменьшения θ. Сила перпендикулярна к касательной и вклада в это уравнение не дает. Уравнение движения примет вид
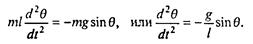(7.28)
Обычно в курсе физики ограничиваются исследованием малых колебаний. Если | θ |<< 1, то уравнение (7.28) можно считать эквивалентным (так как sin θ ≈ θ; здесь и далее используется радианная мера углов) уравнению
Решение его элементарно:
где 
- собственная частота, 
- период колебания маятника. Значения А и В зависят от начальных условий. Если при t = 0
то
или, как часто записывают,
где φ - так называемая, начальная фаза; А - амплитуда колебания; А и φ легко выразить через начальные условия θ0 и v0.
Движение, происходящее по закону (7.29), называют гармоническим колебательным движением. Слово «гармонический» связывают с простой тригонометрической функцией (синусом или косинусом); так, гармоническим является и движение A sin (ωt + φ), к которому также можно свести (7.29) (оно отличается лишь сдвигом фазы на π/ 2).
Для изучения колебаний с большой амплитудой следует обратиться к уравнению (7.28), которое заведомо не интегрируется в элементарных функциях. Обезразмерим его, взяв за характерный масштаб времени период малого колебания. Если τ = t/T, то
(7.30)
Это уравнение вообще не содержит параметров! Достаточно его решить, и мы составим полное представление о природе «больших» колебаний. В этом проявляется сила приема обезразмернвания.
Сведем (7.30) к системе двух уравнений первого порядка:
(7.31)
Существенно, что система консервативна, и полная энергия сохраняется (до тех пор, пока мы не учитываем трение и воздействие извне):
|
|
|
(7.32)
В безразмерных переменных x и θ
(7.33)
Как и при моделировании движения небесных тел, сохранение ε в ходе интегрирования - прекрасный критерий для изучения устойчивости метода, выбора шага и т.д. На рис. 7.18 представлен график зависимости θ(τ) для θ0 = π /2 и v0 = 0 (сплошная линия). На первый взгляд, это косинусоида (7.29), но, во-первых, это не так (зрительным впечатлениям в таких случаях доверять особо не следует), а, во-вторых, у этого движения период отнюдь не определяется формулой, следующей из решения задачи о малых колебаниях. Для сравнения на рисунке представлено пунктирной линией гармоническое движение с той же амплитудой π/ 2, следующее из формального решения задачи о малых колебаниях (его период равен единице вследствие обезразмернвания).
Рис. 7.18. Графики зависимости θ(τ) для θ0 = π /2 и v0 = 0 (сплошная линия) и гармонического движения с той же амплитудой π /2 (пунктирная линия)
Итак, реальный период, оказывается, зависит от амплитуды колебания вопреки тому, что предсказывает теория, основанная на приближении малых колебаний. Определить зависимость периода от амплитуды - относительно несложная задача для самостоятельного решения.
Вернемся снова к разговору о периодическом, но не гармоническом движении. Период колебаний в рассмотренном примере приблизительно равен 1,18 (определено в численном эксперименте). Уравнение гармонического движения с периодом Т и амплитудой A
(в нашем конкретном случае A = π /2, T ≈ 1,18, φ = 0). В табл. 7.5 сведены результаты численного решения уравнений (7.31) (вторая строка) и табулирования функции при A = π /2, T ≈ 1,18, φ = 0 (третья строка) на промежутке времени, чуть большем периода. Хотя различия и невелики, но видно, что движение не является гармоническим.
Таблица 7.5
|
|
|
