 |
Формулы модели экономичного размера партии
|
|
|
|
ОСНОВНЫЕ МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ
Теоретическое введение
Модель Уилсона
Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита. Модель Уилсона является простейшей моделью УЗ и описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями:
· интенсивность потребления является априорно известной и постоянной величиной;
· заказ доставляется со склада, на котором хранится ранее произведенный товар;
· время поставки заказа является известной и постоянной величиной;
· каждый заказ поставляется в виде одной партии;
· затраты на осуществление заказа не зависят от размера заказа;
· затраты на хранение запаса пропорциональны его размеру;
· отсутствие запаса (дефицит) является недопустимым.
Входные параметры модели Уилсона
1) 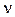 – интенсивность (скорость) потребления запаса, [ед.тов./ед.t];
– интенсивность (скорость) потребления запаса, [ед.тов./ед.t];
2) s – затраты на хранение запаса, [ 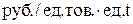 ];
];
3) K – затраты на осуществление заказа, включающие оформление и доставку заказа, [руб.];
4) 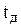 – время доставки заказа, [ед.t].
– время доставки заказа, [ед.t].
Выходные параметры модели Уилсона
1) Q – размер заказа, [ед.тов.];
2) L – общие затраты на управление запасами в единицу времени, [руб./ед.t];
3) 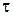 – период поставки, т.е. время между подачами заказа или между поставками, [ед.t];
– период поставки, т.е. время между подачами заказа или между поставками, [ед.t];
4) 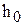 – точка заказа, т.е.размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед.тов.].
– точка заказа, т.е.размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед.тов.].
Циклы изменения уровня запаса в модели Уилсона графически представлены на рис.11.1. Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа Q.
|
|
|
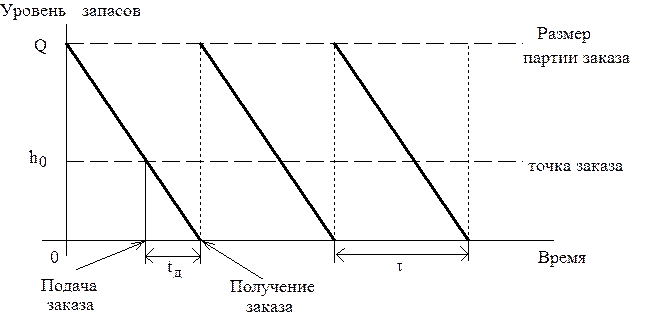
Рис.11.1. График циклов изменения запасов в модели Уилсона
Формулы модели Уилсона
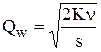 (формула Уилсона), (формула Уилсона),
| (11.1) |
где 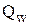 – оптимальный размер заказа в модели Уилсона;
– оптимальный размер заказа в модели Уилсона;
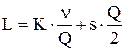 ;
;
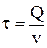 ;
;

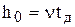 .
.
График затрат на УЗ в модели Уилсона представлен на рис.11.2
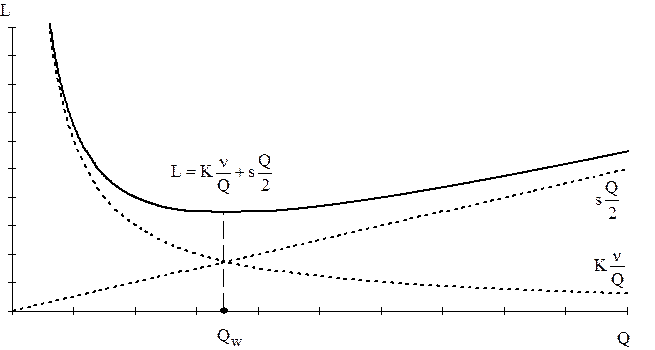
Рис.11.2. График затрат на УЗ в модели Уилсона
11.1.2. Модель планирования экономичного размера партии
Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис.11.3 схематично представлен некоторый производственный процесс. На первом станке производится партия деталей с интенсивностью 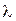 деталей в единицу времени, которые используются на втором станке с интенсивностью
деталей в единицу времени, которые используются на втором станке с интенсивностью 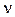 [дет./ед.t].
[дет./ед.t].
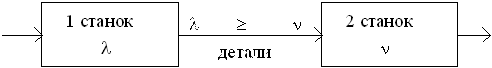
Рис.11.3. Схема производственного процесса
Входные параметры модели планирования экономичного размера партии
1)  – интенсивность производства продукции первым станком, [ед.тов./ед.t];
– интенсивность производства продукции первым станком, [ед.тов./ед.t];
2) 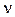 – интенсивность потребления запаса, [ед.тов./ед.t];
– интенсивность потребления запаса, [ед.тов./ед.t];
3) s – затраты на хранение запаса, [ 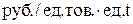 ];
];
4) K – затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.];
5) 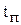 – время подготовки производства (переналадки), [ед.t].
– время подготовки производства (переналадки), [ед.t].
Выходные параметры модели планирования экономичного размера партии
1) Q – размер заказа, [ед.тов.];
2) L – общие затраты на управление запасами в единицу времени, [руб./ед.t];
3) 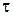 – период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед.t];
– период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед.t];
4) 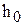 – точка заказа, т.е.размер запаса, при котором надо подавать заказ на производство очередной партии, [ед.тов.].
– точка заказа, т.е.размер запаса, при котором надо подавать заказ на производство очередной партии, [ед.тов.].
Изменение уровня запасов происходит следующим образом (рис.11.4):
· в течение времени 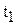 работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запаса накапливается с интенсивностью
работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запаса накапливается с интенсивностью 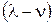 ;
;
|
|
|
· в течение времени 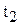 работает только второй станок, потребляя накопившийся запас с интенсивностью
работает только второй станок, потребляя накопившийся запас с интенсивностью 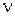 .
.
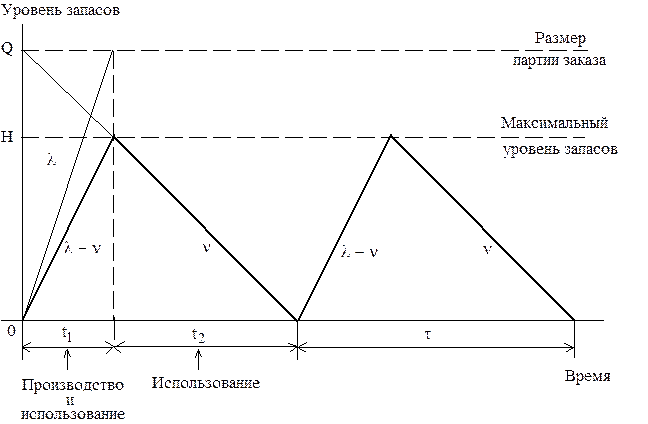
Рис.11.4. График циклов изменения запасов
в модели планирования экономичного размера партии
Формулы модели экономичного размера партии
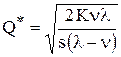 или
или 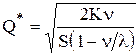 ,
,
где * – означает оптимальность размера заказа;
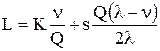 или
или 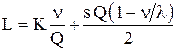 ;
;
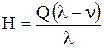 или
или  ;
;
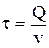 ;
;  .
.
Методические рекомендации
Основная сложность при решении задач по УЗ состоит в правильном определении входных параметров задачи, поскольку не всегда в условии их числовые величины задаются в явном виде. При использовании формул модели УЗ необходимо внимательно следить за тем, чтобы все используемые в формуле числовые величины были согласованы по единицам измерения. Так, например, оба параметра s и 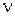 должны быть приведены к одним и тем же временных единицам (к дням, к сменам или к годам), параметры K и s должны измеряться в одних и тех же денежных единицах и т.д.
должны быть приведены к одним и тем же временных единицам (к дням, к сменам или к годам), параметры K и s должны измеряться в одних и тех же денежных единицах и т.д.
Задача №11.01
Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 40 коп. за один пакет. Необходимо определить: сколько пакетов должен заказывать владелец магазина для одной поставки; частоту заказов; точку заказа. Известно, что магазин работает 300 дней в году.
Решение
Примем за единицу времени год, тогда 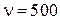 шт. пакетов в год,
шт. пакетов в год, 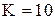 руб.,
руб., 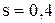
 . Поскольку пакеты супа заказываются со склада поставщика, а не производятся самостоятельно, то будем использовать модель Уилсона.
. Поскольку пакеты супа заказываются со склада поставщика, а не производятся самостоятельно, то будем использовать модель Уилсона.
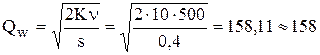 штук.
штук.
Поскольку число пакетов должно быть целым, то будем заказывать по 158 штук. При расчете других параметров задачи будем использовать не 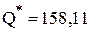 , а Q=158. Годовые затраты на УЗ равны
, а Q=158. Годовые затраты на УЗ равны
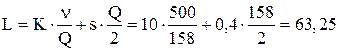 рублей в год.
рублей в год.
Подачу каждого нового заказа должна производиться через
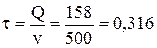 года.
года.
Поскольку известно, что в данном случае год равен 300 рабочим дням, то
|
|
|
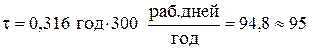 рабочих дней.
рабочих дней.
Заказ следует подавать при уровне запаса, равном
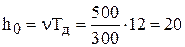 пакетам,
пакетам,
т.е. эти 20 пакетов будут проданы в течение 12 дней, пока будет доставляться заказ.
Задача №11.02
На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 50 коп. в год за одну деталь. Стоимость производства одной детали равна 2,50 руб., а стоимость на подготовку производства составляет 1000 руб. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий?
Решение
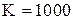 руб.,
руб., 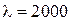 шт. в месяц или 24000 шт. в год,
шт. в месяц или 24000 шт. в год, 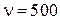 шт. в месяц или 6000 шт. в год,
шт. в месяц или 6000 шт. в год, 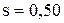 руб. в год за деталь. В данной ситуации необходимо использовать модель планирования экономичного размера партии.
руб. в год за деталь. В данной ситуации необходимо использовать модель планирования экономичного размера партии.
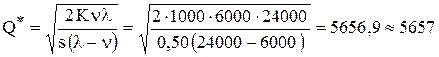 шт.
шт.
Частота запуска деталей в производство равна
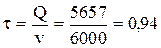 года или 11,28 месяцев.
года или 11,28 месяцев.
Общие затраты на УЗ составляют
 руб. в год.
руб. в год.
Варианты задач для самостоятельного решения
Задача №11.1
Используя график циклов изменения запасов в модели планирования экономичного размера партии (см. рис.11.4), выведите формулы для расчета длительности периодов производства/использования запаса ( 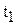 ) и использования запаса (
) и использования запаса ( 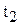 ).
).
Задача №11.2
Постройте график общих годовых затрат на УЗ для задачи №11.01 ( 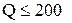 шт.) с учетом затрат владельца магазина на закупку пакетов супа у поставщика (12.1) (см. рис. 11.2). Графически определите наиболее выгодный объем заказа, если суп отпускается упаковками по 90 шт.
шт.) с учетом затрат владельца магазина на закупку пакетов супа у поставщика (12.1) (см. рис. 11.2). Графически определите наиболее выгодный объем заказа, если суп отпускается упаковками по 90 шт.
Задача №11.3
Фирма может производить изделие или покупать его. Если фирма сама выпускает изделие, то каждый запуск его в производство обходится в 20 руб. Интенсивность производства составляет 120 шт. в день. Если изделие закупается, то затраты на осуществление заказа равны 15 руб. Затраты на содержание изделия в запасе независимо от того, закупается оно или производится, равны 2 коп. в день. Потребление изделия фирмой оценивается в 26 000 шт. в год.
|
|
|
Предполагая, что фирма работает без дефицита, определите, что выгоднее: закупать или производить изделие (в месяце 22 рабочих дня).
Задача №11.4
Подтвердите свое решение задачи №11.3 графически, для этого на одном рисунке постройте графики общих затрат фирмы на УЗ (  ) для случаев покупки и производства изделий (см. рис. 11.2).
) для случаев покупки и производства изделий (см. рис. 11.2).
Задача №11.5*
При строительстве участка автодороги длиной 500 м используют гравий, расход которого составляет 120 кг/м. Сроки строительства составляют 17 дней. Работа идет в одну смену. Расход гравия равномерный. Гравий доставляется грузовыми машинами, емкостью 7 т, в течение 4 часов. Затраты на один рейс грузовика равны 15 руб. Затраты на хранение гравия на месте строительства составляют 1 руб. 10 коп. в сутки за тонну.
Определить параметры УЗ: оптимальный объем заказа, количество грузовых машин, используемых для доставки, период поставок, точку заказа, затраты на УЗ за всю стройку. Постройте график двух последних циклов изменения запаса гравия на месте строительства.
Задача №11.6
Подтвердите свое решение задачи №11.5 графически. Для этого отобразите на одном рисунке графики затрат на УЗ для различных вариантов доставки гравия, которые были проанализированы при решении задачи. Покажите на этих графиках оптимальные объемы заказа для каждого из вариантов и окончательно выбранный размер заказа.
Задача №11.7
В течение смены длительностью 24 дня в санатории отдыхают 83 человека. Ежедневно каждый из отдыхающих должен получить 200 г кефира. Кефир на молокозаводе пакуется в пакеты по 0,5 л (6 руб./шт) и 1 л (10 руб./шт) и доставляется транспортом санатория в течение 2 часов. Срок годности кефира ограничен 5 днями. Его хранение в холодильниках санатория обходится в среднем в 12 коп. за 1 л в сутки. Стоимость оформления и доставки заказа составляет 54 руб.
Организуйте поставку кефира в санаторий в течение одной санаторной смены, учитывая в затратах на УЗ (12.1) цену покупки кефира. Постройте график циклов изменения запаса кефира.
Задача №11.8*
Придумайте условие задачи УЗ, максимально приближенное к реальности, для которого могут быть использованы описанные модели УЗ (одна из моделей). Решите эту задачу.
Пример ситуации для задачи: семья из трех человек решает, что выгодней – делать запас картофеля на всю зиму или покупать картофель в течение зимы мелкими партиями. При этом надо учесть такие факторы, как потери картофеля при хранении в домашних условиях, возможное повышение цен на картофель в течение рассматриваемого периода и т.д.
|
|
|


