 |
Раздел 2. Контролные задания и методические указания по их выполнению
|
|
|
|
Раздел 1. ОБЩИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
В соответствии с Государственным образовательным стандартом высшего профессионального образования, утвержденным Министерством образования РФ 13 марта 2000 г., и согласно учебному плану, утвержденному Советом РГАЗУ 27 декабря 2000 г., студенты экономического факультета специальностей 060800 – «Экономика и управление предприятием АПК» и 060500 – «Бухгалтерский учет анализ и аудит» изучают дисциплину «Эконометрика» в объеме 110 часов, выполняют контрольную работу и сдают зачет.
Эконометрика входит в число базовых дисциплин экономического образования современного специалиста сельского хозяйства, изучение которой предполагает получение студентами опыта построения эконометрических моделей, выбора метода оценки параметров модели, получении прогнозных оценок, автокорреляции и др.
Порядок изучения дисциплины следующий. При самостоятельном изучении дисциплины в начале нужно ознакомиться с ее программой. Руководствуясь программой и настоящими методическими указаниями, необходимо приступить к последовательному и глубокому усвоению материала, изложенного в рекомендуемой литературе. При этом следует составить краткий конспект по основным положениям.
После усвоения учебного материала дисциплины выполняется контрольная работа, которую необходимо сдать не позднее чем за два месяца до сессии. Желательно представлять ее в более ранние сроки в целях возможности устранения до сессии отмеченных недостатков, особенно в тех случаях, когда контрольная работа не допущена к собеседованию.
Студент, вызванный на лабораторно-экзаменационную сессию, приносит с собой допущенную к собеседованию контрольную работу. На сессии он посещает лекции и практические занятия, которые охватывают основные разделы программы.
|
|
|
Для изучения дисциплины «Эконометрика» рекомендуется следующая литература.
Библиографический список
Основной
1. Бородич С.А. Эконометрика: Учеб.пособие. – Мн.: Новое знание, 2001.
2. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
3. Практикум по эконометрике: Учеб.пособие. / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
Дополнительный
4. Айвазян С.А., Мхитарян В.С. прикладная статистика и основы эконометрики: Учебник. – М.: Юнити 1998.
5. Джонстон Д. Эконометрические методы. – М.: Статистика, 1997.
6. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1997.
7. Кулинич Е.А. Эконометрия.. – М.: Финансы и статистика, 2000.
8. Ланге О. Введение в эконометрику. – М.: Прогресс, 1964.
9. Лизер С. Эконометрические методы. – М.: Статистика, 1971.
10. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: начальный курс. – М.: Дело, 1997.
11. Маленво Э. Статистические методы эконометрии. – М.: Статистика, 1976.
12. Тинтнер Г. Введение в эконометрию. – М.: Статистика, 1965.
13. Яковлев В.Б. Статистическая обработка данных с применением персональных ЭВМ. Часть 2: Учеб. пособие. – М.: ВСХИЗО, 1993.
Самостоятельное изучение дисциплины может быть успешным при систематических занятиях по учебному графику, при составлении которого целесообразно придерживаться следующих затрат времени на изучение дисциплины (табл. 1).
Таблица 1
Примерное распределение учебного времени по темам дисциплины
(в учебных часах)
| Наименование темы | Всего заочное (очное) | В том числе | Литература | ||
| само-стоя-тель-но | с преподава-телем | ||||
| лек-ции | прак-тики | ||||
| 1. Линейная модель множественной регрессии | 10 () | 7 () | 1 () | 2 () | 1) с. 154-158; 2) с. 90-128; 3) с. 49-105 |
| 2. Метод наименьших квадратов | 10 () | 7 () | 1 () | 2 () | 1) с. 109-120; 2) с. 21-22, 42-43, 63-64, 95, 180, 217; 3) с. 5-6, 49-50, 106-138 |
| 3. Показатели качества регрессии | 10,5 () | 7 () | 1,5 () | 2 () | 1) с. 121-153, 166-198; 2) с. 48-57, 129-141; 3) с. 6-9, 51-56 |
| 4. Свойства оценок метода наименьших квадратов | 7 () | 7 () | – () | – () | 1) с. 63-67, 124, 351-354; 2) с. 155-156 |
| 5. Линейные регрессионные модели с гетероскедастичными и автокорреляционными остатками | 7 () | 6 () | 1 () | – () | 1) с. 230-270, 324-326; 2) с. 156-169, 272-282; 3) с. 55, 139-140 |
| 6. Обобщенный метод наименьших квадратов | 6 () | 6 () | – () | – () | 1) с. 240-244; 2) с. 169-174 |
| 7. Регрессионные модели с переменной структурой | 8 () | 8 () | – () | – () | 2) с. 255-262 |
| 8. Нелинейные модели регрессии и их линеаризация | 6,5 () | 6 () | 0,5 () | – () | 1) с. 200-229; 2) с. 62-83; 3) с. 5-6, 12-14 |
| 9. Характеристики временных рядов | 11,5 () | 7 () | 2,5 () | 2 () | 1) с. 310-345; 2) с. 225-282; 3) с. 137-186 |
| 10. Модели стационарных и нестационарных временных рядов, их идентификация | 8 () | 8 () | – () | – () | 1) с. 292-295; 2) с. 282-289 |
| 11. Система линейных одновременных уравнений | 18,5 () | 14 () | 2,5 () | 2 () | 1) с. 346-377; 2) с. 177-193, 204-224; 3) с. 106-136 |
| 12. Косвенный, двухшаговый и трехшаговый метод наименьших квадратов | 7 () | 7 () | – () | – () | 1) с. 354-356, 367-369; 2) с. 193-204; 3) с. 107-108 |
| Всего: | () | () | () | () |
Раздел 2. КОНТРОЛНЫЕ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ
|
|
|
Задание для контрольной работы содержит две задачи. Номера вариантов определяются в таблицах с исходными данными по последней и предпоследней цифрам номера зачетной книжки.
Для облегчения выполнения заданий по ним даны краткие методические указания.
Контрольное задание желательно выполнить в ученической тетради. При решении задач следует привести формулы, развернутый арифметический расчет с краткими пояснениями и анализ полученных результатов. Страницы работы должны быть пронумерованы и на каждой из них оставлены поля размером 3 – 4 см для замечаний и предложений рецензента. В конце работы приводится список использованной литературы, ставится подпись и дата выполнения.
2.1. КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задача 1
По 10 сельскохозяйственным предприятиям имеются данные о себестоимости молока и средней продуктивности молока (табл. 2 и 3).
Таблица 2
Себестоимость молока, руб./л
| Сельскохозяйственное предприятие | Предпоследняя цифра номера зачетной книжки | |||||||||
| 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | |
| 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | |
| 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | |
| 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | |
| 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | |
| 6,9 | 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | |
| 7,8 | 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | |
| 7,0 | 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | |
| 5,9 | 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | |
| 8,0 | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 |
|
|
|
Таблица 3
Средняя продуктивность молока, кг
| Сельскохозяйственное предприятие | Последняя цифра номера зачетной книжки | |||||||||
Требуется:
1. Рассчитать параметры уравнения парной линейной регрессии зависимости себестоимости молока от средней продуктивности.
2. Оценить качество уравнения с помощью средней ошибки аппроксимации.
3. Найти средний (обобщающий) коэффициент эластичности.
4. Оценить тесноту связи с помощью показателей корреляции и детерминации.
5. Оценить значимость коэффициента корреляции через t-критерий Стьюдента при α = 0,05.
6. Оценить статистическую надежность результатов регрессионного анализа с помощью F-критерия Фишера при α = 0,05.
7. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10 % от его среднего уровня.
Задача 2
По 30 сельскохозяйственным предприятиям имеются данные о средних значениях и вариации урожайности зерновых, количестве внесенных удобрений и насыщенности севооборота зерновыми, а также о значениях коэффициентов парной корреляции между этими признаками (табл. 4 и 5).
|
|
|
Таблица 4
Урожайность зерновых, количество внесенных удобрений и продолжительность вегетационного периода
| Предпо-следняя цифра номера зачетной книжки | Урожайность зерновых, ц/га | Внесено органических удобрений, ц/га | Насыщенность севооборота зерновыми, % | |||
| Среднее значе-ние | Среднее квадратиче-ское откло-нение | Среднее значе-ние | Среднее квадратиче-ское откло-нение | Среднее значе-ние | Среднее квадратиче-ское откло-нение | |
| 
| 
| 
| 
| 
| |
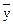
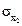
| 12,5 | 5,0 | 1,5 | 8,0 | |||
| 13,5 | 5,4 | 1,7 | 8,5 | |||
| 15,0 | 5,8 | 1,9 | 9,0 | |||
| 16,0 | 6,2 | 2,1 | 9,5 | |||
| 16,5 | 6,6 | 2,3 | 10,0 | |||
| 17,0 | 7,0 | 2,5 | 10,5 | |||
| 17,5 | 7,4 | 2,7 | 11,0 | |||
| 18,5 | 7,8 | 2,9 | 11,5 | |||
| 21,5 | 8,2 | 3,1 | 12,0 | |||
| 22,0 | 8,6 | 3,3 | 12,5 |
Таблица 5
Линейные коэффициенты парной корреляции
| Последняя цифра номера зачетной книжки | 
| 
| 
|
| 0,33 | 0,48 | 0,04 | |
| 0,34 | 0,46 | 0,05 | |
| 0,35 | 0,44 | 0,06 | |
| 0,36 | 0,42 | 0,07 | |
| 0,37 | 0,40 | 0,08 | |
| 0,38 | 0,38 | 0,09 | |
| 0,39 | 0,36 | 0,10 | |
| 0,40 | 0,34 | 0,11 | |
| 0,41 | 0,32 | 0,12 | |
| 0,42 | 0,30 | 0,13 |
Требуется:
1. Построить уравнение множественной линейной регрессии зависимости урожайности зерновых от количества внесенных удобрений и насыщенности севооборота зерновыми.
2. Определить линейный коэффициент множественной корреляции.
3. Рассчитать общий F-критерий Фишера при уровне значимости α = 0,05.
2. 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНЫХ ЗАДАНИЙ
Методические указания к задаче 1
Пример
По 10 сельскохозяйственным предприятиям имеются данные о себестоимости молока и средней продуктивности молока (табл. 6).
Таблица 2
| Себестоимость молока, руб./л | 7,5 | 6,0 | 5,2 | 8,3 | 5,8 | 6,9 | 7,8 | 7,0 | 5,9 | 8,0 |
| Средняя продук-тивность молока, кг |
Требуется:
1. Рассчитать параметры уравнения парной линейной регрессии зависимости себестоимости молока от средней продуктивности.
2. Оценить качество уравнения с помощью средней ошибки аппроксимации.
3. Найти средний (обобщающий) коэффициент эластичности.
4. Оценить тесноту связи с помощью показателей корреляции и детерминации.
5. Оценить значимость коэффициента корреляции через t-критерий Стьюдента при α = 0,05.
6. Оценить статистическую надежность результатов регрессионного анализа с помощью F-критерия Фишера при α = 0,05.
7. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10 % от его среднего уровня.
Решение
1. Уравнение парной линейной регрессии имеет вид:
ŷх = а + bх,
где ŷх – себестоимость молока, руб./л;
|
|
|
х – средняя продуктивность молока, кг;
а, b – параметры уравнения.
Для определения параметров уравнения а и b составим систему нормальных уравнений. Исходное уравнение последовательно умножим на коэффициенты при неизвестных а и b, и затем каждое уравнение просуммируем:
,
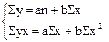где n – число единиц совокупности.
Для расчетов построим вспомогательную таблицу (табл. 7).
Таблица 7
| Сельскохозяйственное предприятие | Себестоимость молока, руб./л | Средняя продуктивность молока, кг | у2 | х2 | ху | ŷх | у- ŷх | 
|
| у | х | |||||||
| 7,5 | 56,25 | 1477,5 | 6,96 | 0,54 | 7,2 | |||
| 6,0 | 36,00 | 1008,0 | 6,25 | -0,25 | 4,1 | |||
| 5,2 | 27,04 | 702,0 | 5,44 | -0,24 | 4,6 | |||
| 8,3 | 68,89 | 2149,7 | 8,48 | -0,18 | 2,1 | |||
| 5,8 | 33,64 | 875,8 | 5,83 | -0,03 | 0,5 | |||
| 6,9 | 47,61 | 1283,4 | 6,69 | 0,21 | 3,1 | |||
| 7,8 | 60,84 | 1817,4 | 7,84 | -0,04 | 0,5 | |||
| 7,0 | 49,00 | 1491,0 | 7,35 | -0,35 | 5,0 | |||
| 5,9 | 34,81 | 867,3 | 5,73 | 0,17 | 2,9 | |||
| 8,0 | 64,00 | 1872,0 | 7,86 | 0,14 | 1,7 | |||
| Сум-ма | 68,4 | 478,09 | 13544,1 | × | × | 31,7 |
Подставим полученные данные в систему уравнений:
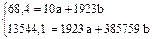
Разделим каждый член уравнений на коэффициенты при а (в первом уравнении на 10, во втором на 1925):
Вычтем из второго уравнения первое и найдем параметр b:
0,203 = 8,3b; b = 0,0245.
Подставив значение b в первое уравнение, найдем значение а:
а = 6,84 – 192,3 · 0,0245 = 2,13.
Параметры уравнения регрессии можно определить и по другим формулам, которые вытекают из системы нормальных уравнений:
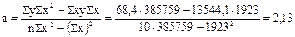
Уравнение регрессии имеет вид:
ŷх = 2,13 + 0,0245х.
Коэффициент регрессии b = 0,0245 показывает, что при росте средней продуктивности молока на 1 кг себестоимость молока в среднем по данной совокупности хозяйств увеличивается на 2,45 копейки за литр.
2. Оценим качество уравнения с помощью средней ошибки аппроксимации по формуле:
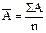
где 
– ошибка аппроксимации.
Подставляя в уравнение регрессии х, определим теоретические (расчетные) значения ŷх (табл. 7). Найдем величину средней ошибки аппроксимации 
. Для этого заполним две последние графы табл. 7. Отсюда:
.
В среднем расчетные значения себестоимости молока отклоняются от фактических на 3,17%. Качество уравнения регрессии можно оценить как высокое, так как средняя ошибка аппроксимации меньше допустимого предела (8-10%).
3. Рассчитаем средний коэффициент эластичности 
по формуле:
где 
и 
– средние значения признаков.
Отсюда:
;
;
.
Коэффициент эластичности показывает, что в среднем при росте средней продуктивности молока на 1% себестоимость молока повышается на 0,69 %.
4. Для определения тесноты связи между исследуемыми признаками рассчитаем коэффициент корреляции. Для парной линейной зависимости формула имеет вид:
,
где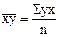 
– средняя сумма произведения признаков;
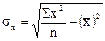и 
– средние квадратические отклонения по х и у.
Данные для расчета коэффициента корреляции представлены в табл. 7 и в пункте 3 решения. Отсюда:
;
;
;
.
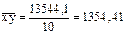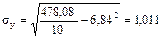Коэффициент корреляции 
свидетельствует, что связь между признаками очень тесная и прямая. Коэффициент детерминации 
показывает, что 93,5 %изменений в уровне себестоимости объясняется различной продуктивностью молока.
5. Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем t-критерий Стьюдента по формуле:
Вычисленное tфакт сравним с табличным (критическим) значением tтабл при принятом уровне значимости α = 0,05 и числе степеней свободы ν = n – 2 = 10 – 2 = 8. Табличное значение по таблице распределения Стьюдента равно 2,306.
Фактическое значение критерия больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между себестоимостью и продуктивностью молока.
6. Оценим значимости уравнения регрессии и показателя тесноты связи с помощью F-критерия Фишера. Для этого сравним его фактическое значение Fфакт с табличным Fтабл.
Фактическое значение Fфакт определяется по формуле:
,
В нашем случае:
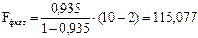
Табличное значение Fфакт по таблице значений F-критерия Фишера при α = 0,05, k1 = m = 1 и k2 = n – m – 1 = 10 – 1 – 1 = 8 равно 5,32 (m – число параметров при переменной х).
Фактическое значение критерия больше табличного, что свидетельствует о статистической значимости уравнения регрессии в целом и показателя тесноты связи 
, то есть они статистически надежны и сформировались под неслучайным воздействием фактора х.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Рассчитаем прогнозное значение себестоимости молока при среднем росте продуктивности молока на 10 %.
Прогнозное значение средней продуктивности молока:
Прогнозное значение себестоимости молока:
ŷр = 2,13 + 0,0245·211,53 = 7,31 руб./л.
Методические указания к задаче 2
Пример
По 30 сельскохозяйственным предприятиям имеются данные о средних значениях и вариации урожайности зерновых, количестве внесенных удобрений и насыщенности севооборота зерновыми, а также о значениях коэффициентов парной корреляции между этими признаками (табл. 8).
Таблица 8
| Показатель | Признак | Среднее значение | Среднее квадратическое отклонение (σ) | Линейные коэффициенты парной корреляции |
| Урожайность зерновых, ц/га | у | 19,5 | 8,4 | =0,405
=0,33,
=0,115
|
| Внесено органических удобрений, ц/га | х1 | 25,0 | 3,2 | |
| Насыщенность севооборота зерновыми, % | х2 | 13,0 |
Требуется:
1. Построить уравнение множественной линейной регрессии зависимости урожайности зерновых от количества внесенных удобрений и насыщенности севооборота зерновыми.
2. Определить линейный коэффициент множественной корреляции.
3. Рассчитать общий F-критерий Фишера при уровне значимости α = 0,05.
Решение
1. Уравнение множественной линейной регрессии имеет вид:
,
где 
– урожайность зерновых с 1 га, ц;
х1 – внесено органических удобрений на 1 га, ц;
х2 – насыщенность севооборота, %;
а, b1 и b2 – параметры уравнения.
Для расчета параметров а, b1 и b2 сначала построим уравнение множественной регрессии в стандартизированном масштабе:
где 
- стандартизированные переменные;
β1 и β2 – стандартизированные коэффициенты регрессии.
Стандартизированные коэффициенты регрессии определим по формулам:
Уравнение множественной регрессии в стандартизированной форме имеет вид:
.
Стандартизированные коэффициенты регрессии позволяют сделать заключение о сравнительной силе влияния каждого фактора на урожайность зерновых. Более значимое влияние оказывает первый фактор, а именно, количество внесенных органических удобрений. В целом же можно сказать, что влияние факторов на урожайность практически одинаково.
Для построения уравнения в естественной форме рассчитаем b1 и b2, используя формулы перехода от βi к bi:
,
где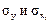 
– средние квадратические отклонения
;
.
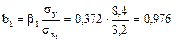Параметр определим из соотношения:
.
Получим уравнение:
.
Каждый из коэффициентов уравнения регрессии определяет среднее изменение урожайности за счет изменения соответствующих факторов и фиксированного уровня другого так, коэффициент при х1 показывает, что увеличение (или снижение) количества внесения удобрений на 1 ц ведет к повышению (или снижению) урожайности зерновых на 0,976 ц. Соответственно коэффициент при х2 определяет меру зависимости урожайности зерновых от насыщенности севооборота.
2. Для определения линейного коэффициента множественной корреляции используем формулу:
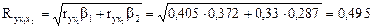
Коэффициент множественной корреляции показывает тесную зависимость между анализируемыми признаками. Коэффициент множественной детерминации 
= 0,4952 = 0,245 свидетельствует, что 24,5% изменения урожайности зерновых связано с анализируемыми признаками.
3. Статистическую значимость уравнения регрессии в целом и показателя тесноты связи оценим с помощью общего F-критерия Фишера по формуле:
где n – число единиц совокупности;
m – число факторов в уравнении линейной регрессии.
В нашем случае:
Табличное значение Fтабл по таблице значений F-критерия Фишера при α=0,05, k1 = m = 2 и k2 = n – m – 1 = 30 – 2 – 1 = 27 равно 3,35.
Фактическое значение критерия больше табличного, что свидетельствует о статистической значимости уравнения регрессии в целом и показателя тесноты связи , которые сформировались под неслучайным воздействием факторов х1 и х2.
ПРИЛОЖЕНИЕ 1
|
|
|
