 |
Как найти наибольший общий делитель
|
|
|
|
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.
Признак делимости на 3
Число делится на 3, когда сумма его цифр делится на 3. Например, число 159 делится на 3, поскольку сумма его цифр 1 + 5 + 9 = 15 делится на 3.
Признак делимости на 4
Число делится на 4, когда две последние цифры нули или составляют число, делящееся на 4. Например, 14676 — последние цифры 76, и число 76 делится на 4: 76:4=19. Двузначное число делится на 4 тогда и только тогда, когда удвоенная цифра в разряде десятков, сложенная с цифрой в разряде единиц, делится на 4. Например, число 42 не делится на 4, так как {\displaystyle 2\cdot 4+2=10} не делится на 4.
Более простая формулировка: Число делится на 4, если в последнем разряде 0, 4, 8, а предпоследний разряд чётный; или если в последнем разряде 2, 6, а предпоследний разряд нечётный.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или на 5.
Признак делимости на 6
Число делится на 6 тогда, когда оно делится и на 2, и на 3 (то есть если оно четное и сумма его цифр делится на 3).
Другой признак делимости: число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с цифрой в разряде единиц, делится на 6.
Признак делимости на 7
Признак 1: число делится на 7 тогда, когда утроенное число десятков, сложенное с цифрой в разряде единиц, делится на 7. Например, 154 делится на 7, так как на 7 делится {\displaystyle 15\cdot 3+4=49.} 1001 делится на 7, так как на 7 делятся {\displaystyle 100\cdot 3+1=301,\quad 30\cdot 3+1=91,\quad 9\cdot 3+1=28,\quad 2\cdot 3+8=14,\quad 1\cdot 3+4=7.}
Признак 2: число делится на 7 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по три цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 7. Например, 138 689 257 делится на 7, так как на 7 делится {\displaystyle \left|138-689+257\right|=294.}
|
|
|
Признак 3: зачеркнув в данном числе три последние цифры, вычитают из числа, образованного оставшимися цифрами, число, образованное зачёркнутыми цифрами (или наоборот, в зависимости от того, какое из них больше); если остаток равен нулю или делится на 7, то данное число разделится на 7
Признак 4: если удвоенное число единиц числа отнять от оставшегося числа десятков, и результат будет делиться на 7, то число кратно 7. Например: 784 делится на 7,так как 78-(2×4)=78-8=70
Признак делимости на 8
Число делится на 8, когда три последние цифры составляют число, делящееся на 8. Трёхзначное число делится на 8 тогда и только тогда, когда цифра в разряде единиц, сложенная с удвоенной цифрой в разряде десятков и учетверённой цифрой в разряде сотен, делится на 8. Например, 952 делится на 8 так как на 8 делится {\displaystyle 9\cdot 4+5\cdot 2+2=48.}
Признак делимости на 9
Число делится на 9, когда сумма его цифр делится на 9. Например, сумма цифр числа 12345678 делится на 9, следовательно и само число делится на 9. {\displaystyle 1+2+3+4+5+6+7+8=36.}
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
103, 105.
Наибольший общий делитель (НОД) двух данных чисел a и b — это наибольшее число, на которое оба числа a и b делятся без остатка.
Кратко наибольший общий делитель чисел a и b записывают так:
Числа 7 и 9 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми числами.
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
1. разложить делители чисел на простые множители;
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.
|
|
|
Поясним сразу на примере. Разложим на простые множители числа 28 и 64.
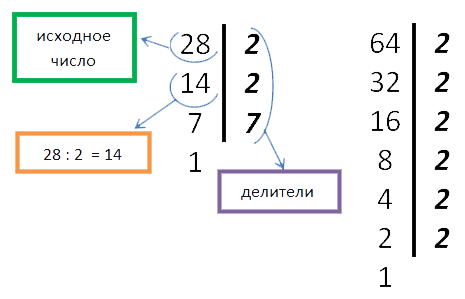
2. Подчёркиваем одинаковые простые множители в обоих числах.
28 = 2 · 2 · 7
64 = 2 · 2 · 2 · 2 · 2 · 2
3. Находим произведение одинаковых простых множителей и записать ответ;
НОД (28; 64) = 2 · 2 = 4
Ответ: НОД (28; 64) = 4
Источник: http://math-prosto.ru
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое самоделится нацело на каждое из этих чисел.
способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
1. Разложить данные числа на простые множители. Подробнее правила разложения на простые множители вы можете прочитать в темекак найти наибольший общий делитель (НОД). 
2. Выписать в строчку множители, входящие в разложениесамого большого из чисел, а под ним — разложение остальных чисел.
Запомните! 
Количество одинаковых множителей в разложениях чисел может быть разное.
60 = 2 · 2 · 3 · 5
24 = 2 · 2 · 2 · 3
3. Подчеркнуть в разложениименьшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2
4. Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).

24 = 2 · 2 · 2 · 3
16 = 2 · 2 · 2 · 2
12 = 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16.
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
104.
Простые числа — это целые числа больше единицы, имеющее ровно два натуральных делителя: 1 и само себя. Таким образом, 6 — это не простое число, так как оно может быть представлено как произведение 2×3, а 5 — это простое число, потому что единственный способ представить его как произведение двух чисел — это 1×5 или 5×1. Если у вас есть несколько монет, но вы не можете расположить их все в форме прямоугольника, а можете только выстроить их в прямую линию, ваше число монет — это простое число.
Последовательность простых чисел начинается с
|
|
|
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, бесконечно.
|
|
|


