 |
Расчет рабочих характеристик
|
|
|
|
Рабочими характеристиками асинхронных двигателей называют зависимости мощности, тока, коэффициента мощности и КПД от скольжения.
Расчет характеристик базируется на системе уравнений токов и напряжений асинхронного двигателя, которому соответствует Г-образная схема замещения.
Активное сопротивление намагничивающего контура r12, Ом, по формуле (9.184) [1]
,
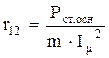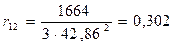(Ом).
Реактивное сопротивление намагничивающего контура х12, Ом, вычисляется по формуле (9.185) [1]
,
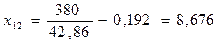(Ом).
Определим угол g, град, по формуле (9.222) [1]
,
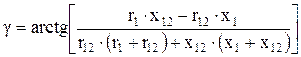(град)
Так как g=0,23 град<1, то для определения коэффициента c1 , можно использовать приближенную формулу (9.223) [1].
Определим коэффициент с1 по формуле (9.223) [1]
,
Активная составляющая тока синхронного холостого хода Iоа, А, определяется по формуле (9.226) [1]
,
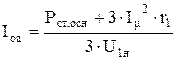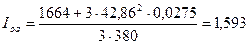(А).
Реактивная составляющая тока синхронного холостого хода Iор , А, определяется по формуле [1]
Iор = Im
I ор= 42,86 (А).
Значение коэффициентов а', b', а, b находим по формулам (9.227) [1]
,
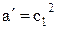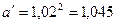(Ом),
,
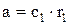(Ом),
,
(Ом),
.
Потери, не изменяющиеся при скольжении 
, Вт, определяются по формуле
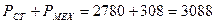(Вт).
Принимаем sн » R'2 = 0,013 и рассчитаем рабочие характеристики по [2]..
Расчет рабочих характеристик сведем в таблицу 11-1, задаваясь s=0,002; 0,004; 0,006; 0,008; 0,01; 0,012; 0,014; 0,016; 0,018; 0,02.
Рабочие характеристики представлены на рисунке 1.
Уточненное значение скольжения sн=0,013.
По данным расчета рабочих характеристик спроектированный двигатель обладает КПД и коэффициентом мощности выше представленных в техническом задании.
Таблица 11-1 - Данные расчета рабочих характеристик асинхронного двигателя с короткозамкнутым ротором
Р2н=200 кВт, U1н=380 В, 2р=4, I1н=202,87 А, Вт, Рдобн=1064 Вт, Iоа=1,593 А, Iор=42,86 А, r1=0,0275 Ом, r'2=0,0292 Ом, с1=1,02, a'=1,045 Ом, а=0,028 Ом, b'=0, b=0,341 Ом.
|
|
|
| Расчетная формула | Ед. | Скольжение | ||||||
| 0,002 | 0,004 | 0,006 | 0,008 | 0,013 | 0,02 | |||
| Ом | 12..49 | 6.26 | 4.183 | 3.144 | 1.95 | 1.275 | |
| Ом | 0.3411 | 0.3411 | 0.3411 | 0.3411 | 0.3411 | 0.3411 | |
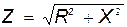
| Ом | 12..49 | 6.269 | 4.197 | 3.163 | 1.975 | 1.319 | |
| А | 30,41 | 60,61 | 90.55 | 120.16 | 192..38 | 288.02 | |
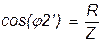
| - | 0,999 | 0,998 | 0,996 | 0,994 | 0,985 | 0,966 | |
| - | 0,027 | 0,054 | 0,081 | 0,108 | 0,173 | 0,259 | |
| А | 31,9 | 62,1 | 91,8 | 121,1 | 191,1 | 279,8 | |
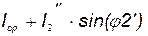
| А | 43,7 | 46,2 | 50,2 | 55,8 | 76,8 | 117,3 | |
| А | 54,2 | 77,4 | 104,7 | 133,7 | 205,7 | 303,4 | |
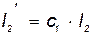
| А | 31,1 | 61,9 | 92,5 | 122,8 | 196,6 | 294,4 | |
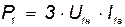
| кВт | |||||||
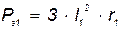
| кВт | 0,24 | 0,5 | 0,9 | 1,5 | 3,5 | 7,6 | |
| кВт | 0,07 | 0,3 | 0,6 | 1,1 | 2,8 | 6,2 | |
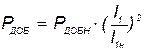
| Вт | |||||||
| кВт | 3,5 | 4,1 | 4,9 | 6,1 | 10,4 | 19,3 | |
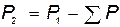
| кВт | 66,8 | 99,8 | 131,9 | 207,4 | 299,7 | ||
| - | 0,91 | 0,943 | 0,953 | 0,956 | 0,952 | 0,939 | |
| - | 0,591 | 0,803 | 0,877 | 0,908 | 0,929 | 0,922 |
12 Расчет пусковых характеристик
Рассчитаем точки характеристик, соответствующих скольжениям s от 1 до значения, соответствующего режиму, близкому к номинальному. Расчет проведем по [2].
12.1 Расчёт токов с учётом влияния изменения параметров под влиянием эффекта вытеснения тока (без участия влияния насыщения от полей рассеяния)
Приведём подробный расчёт для s = 1. Данные расчёта остальных точек сведены в таблицу 12-1.
Таблица 12-1 – Данные расчёт токов в пусковом режиме асинхронного двигателя с короткозамкнутым ротором с учётом влияния эффекта вытеснения тока
| Расчётная формула | Раз-мер-ность | Скольжение s | ||||||
| 0,8 | 0,6 | 0,4 | 0,2 | 0,1 | sкр=0,11 | |||
| - | 2,338 | 2,091 | 1,811 | 1,478 | 1,045 | 0,739 | 0,775 |
| - | 1,27 | 0,9 | 0,65 | 0,34 | 0,12 | 0,09 | 0,092 |
| мм | 16,189 | 19,342 | 22,685 | 27,425 | 32,813 | 33,716 | 33,654 |
| - | 2,393 | 1,982 | 1,675 | 1,37 | 1,132 | 1,1 | 1,102 |
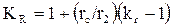
| - | 1,906 | 1,639 | 1,439 | 1,24 | 1,086 | 1,065 | 1,066 |
| Ом | 0,086 | 0,074 | 0,065 | 0,056 | 0,049 | 0,048 | 0,048 |
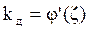
| - | 0,65 | 0,75 | 0,81 | 0,89 | 0,95 | 0,98 | 0,97 |
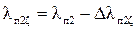
| - | 2,261 | 2,518 | 2,672 | 2,878 | 3,033 | 3,11 | 3,084 |
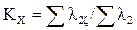
| - | 0,844 | 0,888 | 0,915 | 0,951 | 0,978 | 0,991 | 0,987 |
Продолжение таблицы 12-1 – Данные расчёт токов в пусковом режиме асинхронного двигателя с короткозамкнутым ротором с учётом влияния эффекта вытеснения тока
| Расчётная формула | Раз-мер-ность | Скольжение s | ||||||
| 0,8 | 0,6 | 0,4 | 0,2 | 0,1 | sкр=0,11 | |||
| Ом | 0,221 | 0,233 | 0,24 | 0,25 | 0,257 | 0,26 | 0,259 |
| Ом | 0,129 | 0,136 | 0,153 | 0,184 | 0,292 | 0,533 | 0,488 |
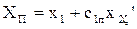
| Ом | 0,447 | 0,459 | 0,466 | 0,476 | 0,483 | 0,487 | 0,485 |
| А | 816,5 | 793,8 | 774,1 | 744,8 | 673,5 | 526,8 | 551,8 |
| А | 830,7 | 808,4 | 788,8 | 759,4 | 687,2 | 537,97 | 563,4 |
|
|
|
Активное сопротивление обмотки ротора с учётом влияния эффекта вытеснения тока [ 
, 
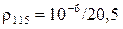Ом·м; 
; 
Гц];
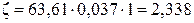
Для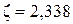 
принимаем из рисунка 9.57 [1] 
.
Глубина проектирования тока hr, мм, определяется по формуле (9.246) [1]
(м) = 16 (мм);
Площадь сечения qr, мм2, определяется по формуле (9.253) [1]
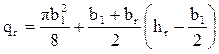(12.1)
где
;
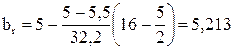(мм).
По (12.1) получим
(мм2);
Коэффициент kr определяется по формуле (9.247) [1]
;
.
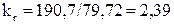Коэффициент общего увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока KR определяется по формуле (9.257) [1]
(12.2)
где 
(Ом); 
(Ом).
По (12.2) получим
.
Приведенное сопротивление ротора с учётом влияния вытеснения тока
;
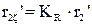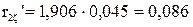(Ом).
Коэффициент изменения индуктивного сопротивления обмотки ротора К Х с учётом влияния эффекта вытеснения тока по рисунку 9.58 [1] для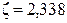 
по (9.262) [1]
(12.3)
где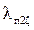 
- коэффициент магнитной проводимости пазового рассеяния с учетом эффекта вытеснения тока
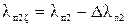(12.4)
здесь
;
.
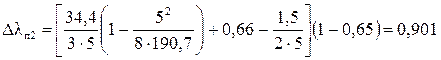По (12.4) получим
.
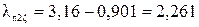По (12.3) получим
.
Приведенное индуктивное сопротивление фазы обмотки ротора от действия эффекта вытеснения тока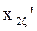 
, Ом, определяется по формуле (9.261) [1]
;
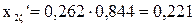(Ом).
Пусковые параметры по (9.277) [1] и (9.278)[1]
;
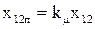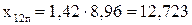(Ом);
;
.
Расчёт токов с учётом влияния эффекта вытеснения тока по (9.280) [1] для s=1
;
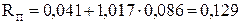(Ом);
;
(Ом).
Ток в обмотке ротора I2п′, А, определяется по формуле (9.281)[1]
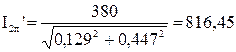А;
Ток в обмотке статора I1п, А, определяется по формуле (9.283)[1]
;
А.
12.2 Расчёт пусковых характеристик с учётом влияния вытеснения токов и насыщения от полей рассеяния
Расчёт проводим для точек характеристик, соответствующих s = 1; 0,8; 0,6; 0,4; 0,2; 0,1, при этом используем значения токов и сопротивлений для тех же скольжений с учётом влияния вытеснения тока.
Данные расчёта сведены в таблицу 12-2. Подробный расчёт приведен для s=1.
Таблица 12-2 – Данные расчёта пусковых характеристик асинхронного двигателя с короткозамкнутым ротором с учётом эффекта вытеснения тока и насыщения от полей рассеяния
| Расчётная формула | Раз-мер-ность | Скольжение s | ||||||
| 0,8 | 0,6 | 0,4 | 0,2 | 0,1 | sкр= =0,11 | |||
| - | 1,35 | 1,3 | 1,25 | 1,2 | 1,15 | 1,1 | 1,11 |
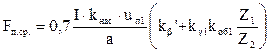
| А | |||||||
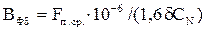
| Тл | 4,215 | 3,949 | 3,706 | 3,425 | 2,97 | 2,224 | 2,35 |
| - | 0,56 | 0,59 | 0,62 | 0,65 | 0,71 | 0,82 | 0,8 |
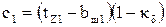
| мм | 6,15 | 5,731 | 5,311 | 4,892 | 4,053 | 2,516 | 2,796 |
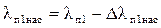
| - | 1,213 | 1,217 | 1,221 | 1,225 | 1,234 | 1,254 | 1,25 |
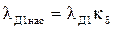
| - | 0,665 | 0,701 | 0,737 | 0,772 | 0,844 | 0,974 | 0,951 |
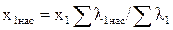
| Ом | 0,185 | 0,187 | 0,19 | 0,192 | 0,197 | 0,206 | 0,204 |
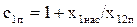
| - | 1,015 | 1,015 | 1,015 | 0,015 | 1,015 | 1,016 | 1,016 |
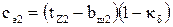
| мм | 7,317 | 6,818 | 6,319 | 5,821 | 4,823 | 2,993 | 3,326 |
|
|
|
Продолжение таблицы 12-2 – Данные расчёта пусковых характеристик асинхронного двигателя с короткозамкнутым ротором с учётом эффекта вытеснения тока и насыщения от полей рассеяния
| Расчётная формула | Раз-мер-ность | Скольжение s | ||||||
| 0,8 | 0,6 | 0,4 | 0,2 | 0,1 | sкр= =0,11 | |||
| - | 1,597 | 1,862 | 2,026 | 2,242 | 2,422 | 2,577 | 2,533 |
| - | 0,702 | 0,727 | 0,763 | 0,8 | 0,874 | 1,01 | 0,985 |
| Ом | 0,166 | 0,18 | 0,189 | 0,201 | 0,213 | 0,226 | 0,223 |
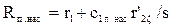
| Ом | 0,129 | 0,135 | 0,153 | 0,184 | 0,291 | 0,532 | 0,488 |
| Ом | 0,354 | 0,37 | 0,382 | 0,396 | 0,413 | 0,435 | 0,43 |
| А | 964,5 | 923,9 | 870,6 | 752,5 | 552,8 | 584,1 | |
| А | 978,2 | 937,8 | 884,4 | 765,2 | 563,1 | 594,7 | |
| - | 1,23 | 1,21 | 1,19 | 1,17 | 1,11 | 1,05 | 1,06 |
| - | 6,1 | 5,83 | 5,59 | 5,27 | 4,56 | 3,36 | 3,55 |
| - | 1,58 | 1,56 | 1,69 | 1,92 | 2,513 | 2,66 | 2,7 |
Перед началом расчёта задаются примерным значением кратности увеличения тока, обусловленной уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны.
,
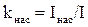где I – ток, рассчитанный для данного режима без учёта насыщения;
Iнас – ток в этом же режиме работы машины при насыщении участков зубцов полями рассеяния.
Ориентировочно принимаем kнас = 1,35.
Средняя МДС обмотки, отнесённую к одному пазу обмотки статора, Fп.ср, А, определяется по формуле (9.263) [1]
;
(А).
Индукция потока рассеяния в воздушном зазоре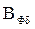 
, Тл, определяется по формуле (9.264) [1]
(12.5)
где коэффициент CN определяется по формуле (9.265) [1]
;
.
По (12.5) получим
.
По рисунку 9.61 [1] для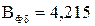 
Тл находим 
.
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учётом влияния насыщения c1 определяется по формуле (9.266) [1]
;
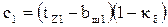(мм);
Для полуоткрытого паза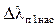 
определяется по формуле (9.269) [1]
;
;
;
.
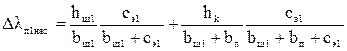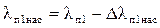Коэффициент магнитной проводимости дифференциального рассеяния обмотки статора с учётом влияния насыщения 
определяется по формуле (9.274) [1]
|
|
|
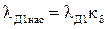
Индуктивное сопротивление фазы обмотки статора с учётом влияния насыщения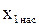 
определяется по формуле (9.275) [1]
;
(Ом).
Коэффициент магнитной проводимости пазового рассеяния обмотки ротора с учетом влияния насыщения и вытеснения тока 
определяется по формуле (9.271) [1]
(12.6)
где коэффициент c2 определяется по формуле (9.270) [1]
;
.
По (12.6) получаем
.
Для ротора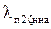 
определяется по формуле (9.273) [1]
;
.
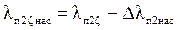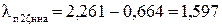Коэффициент магнитной проводимости дифференциального рассеяния ротора с учётом влияния насыщения 
определяется по формуле (9.274) [1]
;
.
Приведенное индуктивное сопротивление фазы обмотки ротора с учётом влияния эффекта вытеснения тока и насыщения 
, Ом, определяется по формуле (9.276) [1]
(Ом).
Коэффициент с1п.нас определяется по формуле (9.278) [1]
;
.
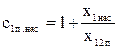Расчёт токов с учётом влияния эффекта вытеснения тока и насыщения от полей рассеяния по (9.280) [1] для s=1
;
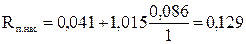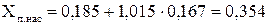(Ом);
;
(Ом);
Ток в обмотке ротора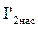 
, А, определяется по формуле (9.281)[1]
;
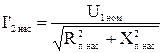(А);
Ток в обмотке статора I1нас, А, определяется по формуле (9.283) [1]
;
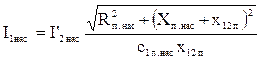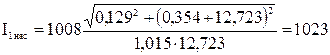(А).
Кратность пускового тока с учётом влияния эффекта вытеснения тока и насыщения
;
.
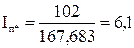Кратность пускового момента с учётом влияния вытеснения тока и насыщения определяется по формуле (9.284) [1]
;
.
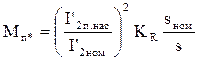Полученный в расчёте коэффициент насыщения
;
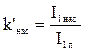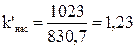
отличается от принятого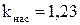 
менее чем на 15 %.
Для расчёта других точек характеристики задаёмся 
, уменьшенным в зависимости от тока 
.
13 Тепловой расчет
Расчет нагрева производят, используя значения потерь, полученных для номинального режима.
Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри двигателя 
, °С, определяется по формуле (9.315) [1]
, (13.1)
где К - коэффициент учитывающий, что часть потерь в сердечнике статора и в пазовой части обмотки передаётся через станину непосредственно в окружающую среду, принимается по таблице 9.35 [1]; К=0,76;
Р'эп1 - электрические потери в обмотке статора в пазовой части при номинальном скольжении sн=0,015351, Вт;
a1-коэффициент теплоотдачи с поверхности по рисунку 9.67, в [1]; a1 =105.
Электрические потери в обмотке статора в пазовой части при номинальном скольжении sн=0,015351 Р'эп1 , Вт, определяются по формуле (9.314) [1]
,
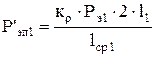где кr - коэффициент увеличения потерь для обмоток с изоляцией F; кr=1,07;
(Вт).
По (13.1) получим
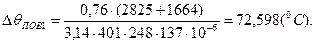
Перепад температуры в изоляции пазовой части обмотки статора 
, °С, определяется по формуле (9.316) [1]
,
где bиз1 - односторонняя толщина изоляции в пазу, мм, bиз1 = 1,9;
lэкв- средняя эквивалентная теплопроводность пазовой изоляции, Вт·/(м·°С);
Пп1 - расчетный периметр поперечного сечения паза статора, мм.
|
|
|
Средняя эквивалентная теплопроводность пазовой изоляции lэкв, Вт·/(м·°С), для класса нагревостойкости F; lэкв =0,16 Вт·/(м·°С);
Расчетный периметр поперечного сечения паза статора Пп1 мм, для полуоткрытых прямоугольных пазов определяется по формуле (9.317) [1]
,
(мм)
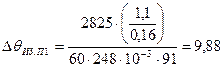(°С).
Перепад температуры по толщине изоляции лобовых частей 
, °С, вычисляется по формуле (9.319) [1]
, (13.2)
где bиз.л1-толщина односторонней изоляции лобовой части катушки; bиз.л1=0,05;
Пл1-периметр условной поверхности охлаждения лобовой части катушки; Пл1 = Пп1 = 91мм;
Р'эл1 - электрические потери в обмотке статора в лобовой части, Вт.
Электрические потери в обмотке статора в лобовой части Р'эл1, Вт, определяются по формуле (9.314) [1]
,
(Вт).
По (13.2) получим
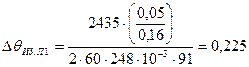(°С)
Превышение температуры наружной поверхности лобовых частей обмотки над температурой воздуха внутри машины 
, °С, определяется по формуле (9.320) [1]
,
(°С).
Среднее превышение температуры обмотки статора над температурой воздуха внутри машины, 
, °С, определяется по формуле (9.321) [1]
,
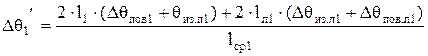(°С).
Превышение температуры воздуха внутри машины над температурой окружающей среды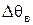 
, °С, определяется по формуле (9.322) [1]
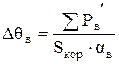, (13.3)
где 
-сумма потерь, отводимых в воздух внутри двигателя, Вт; Sкор- эквивалентная поверхность охлаждения корпуса, мм2;
aв-коэффициент подогрева воздуха по рисунку 9.67, в [1];
aв =1000 
.
Сумма потерь, отводимых в воздух внутри двигателя 
, Вт, определяется по формуле (9.326) [1]
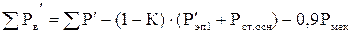, (13.4)
где 
- сумма всех потерь в двигателе при номинальном режиме и расчетной температуре с учетом их увеличения, Вт.
Сумма всех потерь в двигателе при номинальном режиме и расчетной температуре с учетом их увеличения 
, Вт, определяется по формуле (9.324) [1]
, (13.5)
где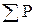 
- сумма всех потерь в двигателе при номинальном режиме и расчетной температуре.
Эквивалентная поверхность охлаждения корпуса Sкор, м2, определяется по формуле (9.327) [1]
,
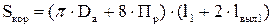Тогда получим
.
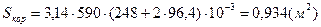По (13.5) получим
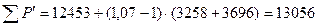(Вт).
По (13.4) получим
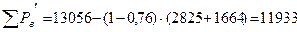(Вт).
По (13.3) получим
Среднее превышение температуры обмотки статора над температурой окружающей среды 
, °С, определяется по формуле (9.328) [1]
,
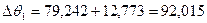(°С).
Среднее превышение температуры обмотки статора над температурой окружающей среды меньше допустимого.
14 Вентиляционный расчет
Требуемый для охлаждения расход воздуха Qв, м 3/с, определяется по формуле (9.340) [1]
,
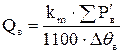где km – коэффициент, учитывающий изменение условий охлаждения по длине поверхности корпуса, обдуваемого наружным вентилятором, определяется по формуле (9.341) [1]
,
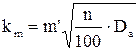где m΄=2,5 [1] для двигателей с 2p≥4 при h≥160 мм
.
Тогда
(м 3/с).
Расход воздуха, который может быть получен при данных размерах двигателя, оценивается эмпирической формулой (9.339) [1]
,
где m` - коэффициент, учитывающий суммарное воздействие всех нагнетательных элементов, m`=10.
(м 3/с).
Расход воздуха обеспечиваемый конструкцией ротора Q'в = 3,267 м 3/с больше требуемого для охлаждения расхода воздуха Qв = 0,849 м 3/с.
15 Вывод
Спроектированный мной электрический двигатель 4А315М4 отвечает поставленным в техническом задании требованиям. Энергетические показатели данного двигателя выше показателей своего аналога, а нагрев обмоток двигателя находится в допустимых пределах. Расход воздуха, обеспечиваемый конструкцией ротора, больше требуемого для охлаждения расхода воздуха.
Литература
1. Копылов И.П. Проектирование электрических машин: Учебник для вузов. – 3-е изд., испр. и доп. – М.: Высшая школа,2002.-757 с.: ил.
2. Вигриянов П.Г., Воронин С.Г. Расчет характеристик электрических машин: Учебное пособие по курсовому проектированию.-Челябинск: ЧПИ,1986-42 с.
3. Кравчик А.Э. Асинхронные двигатели серии 4А: Справочник.-М. Энергоиздат, 1982.- 504с, ил.
|
|
|
