 |
Определение свободного члена
|
|
|
|
ТЕМА КОНТРОЛЬНОЙ РАБОТЫ
«ВЫБОР И ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ЭКСПЕРИМЕНТА»
Задание:
Определить влияние режимов шлифования (глубина шлифования, скорость движения стола и твердость абразивного инструмента) на результат шлифования образцов из стали (шероховатость обработанной поверхности).
Для выполнения поставленной задачи необходимо выполнить следующее:
1. Выбрать критерий Y, определить факторы и интервалы их варьирования.
2. Построить план проведения полного факторного эксперимента.
3. Определить коэффициенты уравнения регрессии.
4. Проверить значимость коэффициентов регрессии.
5. Вычислить расчетные значений параметров оптимизации.
6. Определить критерий Фишера и проверить модель на адекватность.
7. Cделать вывод о влиянии режимов шлифования на результат.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. ВЫБОРКА Y, ОПРЕДЕЛЕНИЕ ФАКТОРОВ И ИНТЕРВАЛОВ ИХ ВАРЬИРОВАНИЯ
Выбор критерия
Критерий (Y): результат шлифования образцов из стали, значение параметра шероховатости.
Определение факторов
Факторы:
1) X 1 − глубина шлифования, мкм/ход.;
2) X 2 − скорость движения стола, м/мин.;
3) X 3 − твердость абразивного инструмента.
Определение интервалов изменения факторов
Область определения факторов устанавливается согласно условиям эксперимента. Схема полно-факторного эксперимента предусматривает одновременное варьирование всех исследуемых факторов на двух уровнях: верхнем (max), имеющем максимальное значение рассматриваемого фактора и нижнем (min), соответствующем минимальному значению фактора. Интервалы изменения факторов в эксперименте представлены в таблице 1.
|
|
|
Таблица 1 − Интервалы варьирования факторов в эксперименте
| Факторы | Уровни | |
| min (-1) | max (+1) | |
| Глубина шлифования– X 1 | 10 мкм/ход. | 20 мкм/ход. |
| Скорость стола – X 2 | 6 м/мин. | 12 м/мин. |
| Твердость круга– X 3 | K | L |
ПОСТРОЕНИЕ ПЛАНА ПРОВЕДЕНИЯ ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА
При известном значении числа факторов, можно найти число опытов, необходимых для реализации всех возможных сочетаний уровней факторов.
, (2.1)
где 
− количество экспериментов,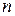 
− число факторов эксперимента.
Подставив значение числа факторов, вычислим количество экспериментов по (2.1):
План эксперимента удобно задавать таблицей, называемой матрицей планирования эксперимента, включающей в себя значения факторов и эффектов их взаимодействий, а также значения исследуемой функции, называемой параметром оптимизации. Матрица планирования полнофакторного эксперимента типа 
и результаты опытов представлены в таблице 2. В таблице и в дальнейшем применяем сокращенное обозначение уровней факторов: вместо +1 и −1 обозначаем + и −.
Из таблицы 1 приложения в соответствии со списком группы или по согласованию с преподавателем выбираются значения Y эксп и заносятся в таблицу 2.
Таблица 2 − Матрица планирования полнофакторного эксперимента типа с эффектом взаимодействия первого порядка и результаты опытов
| Номер опыта, N k | Порядок варьирования факторов | Значения параметра оптимизации | ||||||||
| x 1 | x 2 | x 3 | x 1 x 2 | x 1 x 3 | x 2 x 3 | Y эксп | Y расч | ∆ Y | (∆ Y)2 | |
| + | + | + | + | + | + | 0,81 | 0,84 | 0,028 | 0,0008 | |
| − | + | + | − | − | + | 0,66 | 0,65 | -0,007 | 0,0001 | |
| + | − | + | − | + | − | 0,98 | 0,93 | -0,053 | 0,0028 | |
| − | − | + | + | − | − | 0,85 | 0,88 | 0,033 | 0,0011 | |
| + | + | − | + | − | − | 0,95 | 0,92 | -0,028 | 0,0008 | |
| − | + | − | − | + | − | 0,73 | 0,74 | 0,007 | 0,0001 | |
| + | − | − | − | − | + | 0,96 | 1,01 | 0,053 | 0,0028 | |
| − | − | − | + | + | + | 0,97 | -0,033 | 0,0011 | ||
| b i | 0,0575 | -0,08 | -0,0425 | 0,035 | 0,0125 | -0,01 | ||||
| 0,8675 | 0,8675 |
|
|
|
Таким образом, построен полный факторный эксперимент . Он имеет восемь опытов и включает все возможные комбинации уровней трех факторов.
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ
РЕГРЕССИИ
Для полного факторного эксперимента типа уравнение регрессии с учетом эффектов взаимодействия можно представить следующим выражением:
(3.1)
или
, (3.2)
где 
− свободный член уравнения регрессии; 
− коэффициент линейного эффекта, 
− коэффициент эффекта парного взаимодействия, 
− число факторов, 
и 
− факторы эксперимента. (Полученные значения b округлять до четвертого знака после запятой)
Получение модели сводится к нахождению по результатам эксперимента значений неизвестных коэффициентов.
Определение свободного члена
Свободный член () характеризует результат шлифования стали в центре плана. Коэффициент вычисляется по следующей формуле:
, (3.3)
где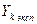 
− параметр оптимизации экспериментальный, − число опытов,
− номер фактора эксперимента,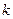 
− номер опыта.
Согласно (3.3) вычислим коэффициент :
|
|
|
