Методы построения оценок (метод моментов, метод максимального правдоподобия)

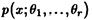Рассмотрим методы определения точечных оценок параметров от которых зависит распределение генеральной совокупности X.

 

В математической статистике разработано большое число методов оценивания неизвестных параметров по данным случайной выборки, из которых в приложениях наиболее часто используются:

 

- метод моментов;

- метод максимального правдоподобия;

 

Мы рассмотрим

 

Метод моментов.

Метод моментов был предложен английским статистиком К. Пирсоном и является одним из первых общих методов оценивания. Он состоит в следующем.

Пусть имеется случайная выборка из генеральной совокупности X, распределение которой 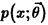известно с точностью до вектора параметров

Требуется найти оценку параметра 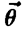по случайной выборке .

 

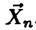Будем предполагать, что у случайной величины X существуют первые r моментов: m_k = EX^k, k=1,2…,r. Ясно, что величины m_k являются функциями неизвестного вектора параметров 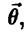, т.е. m_k = m_k ()

 

Рассмотрим выборочные моменты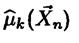

 

Выборочные моменты являются состоятельными оценками соответствующих моментов генеральной совокупности X, поэтому при большом объеме выборки m_k, к= 1,…r, можно заменить соответственно моментами 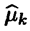и

выборки

В методе моментов в качестве точечной оценки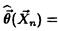

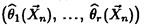
вектора параметров в берут

статистику , значение которой для любой реализации 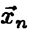случайной

выборки 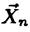получают как решение системы уравнений

k=1,…,r

Можно показать, что при определенных условиях оценка, полученная методом моментов, является состоятельной и имеет асимптотически нормальное распределение, т.е. ее распределение при n→∞ стремится к нормальному.

Замечание 24.10

 

Метод моментов не применим, когда моменты генеральной совокупности нужного порядка не существуют (например, для распределения Коши, у которого не существует даже начальный момент первого порядка — математическое ожидание).

Пример 24.7.

 

Методом моментов найдем оценку параметра θ = p в биномиальной модели, где р есть вероятность „успеха" в любом из п независимых повторных наблюдений, а

случайная величина 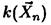— число „успехов". Случайной выборкой 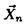в данном случае являются n дискретных случайных величин Х_i, каждая из которых принимает значение 1 с вероятностью р и 0 с вероятностью 1—р. При этом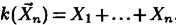

а математическое ожидание 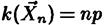.Если в результате n независимых наблюдений мы получили выборочное значение 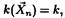, то уравнение, которое нужно составить согласно методу моментов, имеет вид np = k.

Получаем 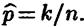. Следовательно, точечной оценкой параметра р является относительная частота.

 

Метод максимального правдоподобия.

Одним из наиболее универсальных методов оценивания параметров является метод максимального правдоподобия (предложенный Р. Фишером), суть которого состоит в следующем.

Рассмотрим функцию правдоподобия случайной выборки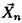

из генеральной совокупности X, распределение 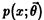которой известно с точностью до параметра в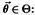

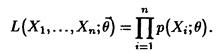
Определение 24.9

Оценкой максимального правдоподобия параметра в называют статистику 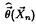, значения в которой для любой выборки х_n удовлетворяют условию 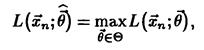, то есть для выборки функция правдоподобия, как функция аргумента 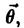достигает наибольшего значения.

Мы исходим из того, что те величины, которые мы наблюдаем, являются наиболее вероятными. Тогда и произведение вероятностей (плотностей) – функция правдоподобия - наблюдаемых значений мы вправе ожидать принимающим наибольшее значение.

 

Как мы помним из математического анализа необходимым условием экстремума является равенство нулю производной (в случае функции нескольких переменных – частной)

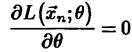но поскольку взятие производной от большого произведения технически сложно, рассматривают не саму функцию правдоподобия, а ее натуральный логарифм 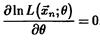, что упрощает уравнение, а точку экстремума оставляет неизменной.

 

Определение 24.10

Эти два уравнения называют уравнениями правдоподобия. Для наиболее важных семейств распределений 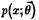уравнение правдоподобия имеет единственное решение .

 

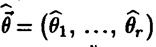Пример 24.8.

Применим метод максимального правдоподобия для оценки параметра θ = р в биномиальной модели, где р имеет смысл вероятности „успеха" в любом из n независимых повторных испытаний (испытаний по схеме Бернулли), в которых было зафиксировано k „успехов".

В рассматриваемом случае значения функции правдоподобия L(k;p) есть вероятность появления к „успехов" в серии из n испытаний. Эта вероятность, как известно, определяется по формуле Бернулли, т.е.

Находя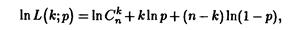

получаем уравнение правдоподобия в виде

'

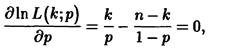откуда получаем 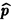= k/n. Нетрудно убедиться в том, что р есть точка максимума L(k;p). Следовательно, оценка максимального правдоподобия вероятности р совпадает с относительной частотой „успеха" в n испытаниях.

Замечание 24.11

Мы рассмотрели метод моментов и метод максимального правдоподобия для дискретных случаев. Для абсолютно непрерывных величин суть методов остается той же, но становится технически более сложной, поэтому мы оставили эту часть за рамками рассмотрения.

 

Интервальные оценки

Любая точечная оценка является функцией выборки, то есть является случайной величиной, а при каждой реализации выборки эта функция определяет единственное значение оценки, принимаемое за приближаемое значение оцениваемой характеристики.

При этом надо принимать во внимание, что в каждом конкретном случае значение оценки может отличаться от значения параметра, поэтому желательно было бы знать и возможную погрешность, возникающую при использовании предлагаемой оценки, например, указывая такой интервал (или область в случае векторного (неодномерного) параметра), внутри которого с высокой (т. е. близкой к 1) вероятностью находится истинное значение оцениваемого параметра. При таком подходе говорят об интервальном или доверительном оценивании. Основная цель при

этом состоит в том, чтобы при заданном доверительном уровне, построить

кратчайший интервал, обеспечивающий наиболее точную локализацию оцениваемой характеристики.

То есть, в некоторых случаях оказывается более важным установить не конкретное число – кандидата на значение неизвестного параметра (точечное оценивание), а указать интервал, в котором с некоторой вероятностью находится искомое неизвестное значение параметра.

Границы этого интервала, называемого доверительным, строятся по выборке, то есть являются оценками (интервальными) данного параметра.

 

Итак, мы хотим найти такие статистики 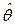^* (Х₁…,Х_n (верхняя доверительная граница) и 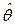_* (Х₁…,Х_n) (нижняя доверительная граница), чтобы с вероятностью α выполнялось равенство

P 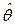_* (Х₁…,Х_n) ≤ θ ≤ 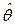^* (Х₁…,Х_n) = α, то есть с заданной вероятностью значение параметра попадало бы в полученный интервал.

Замечание 24.12. Α в разных источниках называется коэффициентом доверия, уровнем доверия, доверительной вероятностью, надежностью.

Замечание 24.13. Иногда задача формулируется немного по-другому: требуют выполнения с вероятностью α неравенства

P (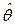 _* (Х₁…,Х_n) ≤ θ ≤ 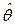^* (Х₁…,Х_n)≥ α, то есть вероятность попасть в интервал для параметра должна быть не меньше α

Сначала задается доверительная вероятность. Обычно ее выбирают равной 0.95, 0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр попал в интервал (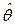 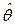_*, ^*) достаточно высока. Число ( 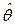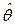_*+ ^*)/ 2 – середина доверительного интервала – будет давать значение параметра θ с точностью ( 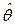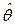_* - ^*)/ 2, которая представляет собой половину длины доверительного интервала.

 

Таким образом, границы доверительного интервала будут зависеть не только от самих наблюдений, но и от их числа n и заданной доверительной вероятности α.

 

 

Определение 24.11

Таким образом, доверительным (для оценки параметра θ, отвечающим доверительной вероятности α) называется такой интервал, который с наперед заданной вероятностью содержит оцениваемый параметр. Границы его θ_* и θ^* будут зависеть от α и от числа наблюдений n

 

 

Замечание 24.14. Как и в случае точечных оценок, получаемые оценки (границы интервала) тем ближе к параметру с тем большей вероятностью, чем больше объем выборки (Напомним, что все характеристики качества оценок рассматриваются при n→∞)

 

Пример 24.9. Пусть θ – среднее значение предела прочности некоторого материала, которое оценивают независимо друг от друга в каждой из N различных лабораторий по результатам n независимых испытаний. Иначе говоря, среднее значение предела прочности в каждой лаборатории оценивают по собственным экспериментальным данным, представленным выборкой объема n, и в каждой лаборатории получают свои значения верхней и нижней границ α-доверительного интервала

 

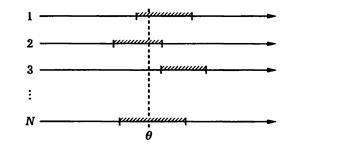
Возможны случаи, когда α-доверительный интервал для параметра θ не накрывает его истинного значения. Если М – число таких случаев, то при больших значениях N должно выполняться приближенное равенство α =(N – M)/N. Таким образом, если опыт – получение выборки объема n в лаборатории, то уровень доверия α – доля тех опытов (при их многократном независимом повторении), в каждом из которых α-доверительный интервал накрывает истинное значение оцениваемого параметра.

 

Напоминание. Оценка 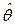(Х₁…,Х_n) называется асимптотически нормальной с дисперсией Δ², если

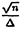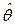( – q) сходится при n →∞ по распределению к стандартному нормальному закону (нормальное распределение при нулевом математическом ожидании и дисперсии, равной 1)

 

 

Асимптотически нормальными являются выборочное среднее, дисперсия, моменты

 

Замечание 24.15.

Построение доверительного интервала основано на определении функции распределения и ее важнейшем свойстве функции распределения: вероятность того, что случайная величина примет значение из промежутка (х ₁; х ₂) равна приращению функции распределения на этом промежутке. P (x ₁ £Х < x ₂) = F (x ₂) – F (x ₁)

Кроме того напомним, что F_Х (α) = P (Х < α). В частности, если некоторая величина имеет стандартное нормальное распределение с функцией распределения N(x), P (x ₁ £Х < x ₂) = N (x ₂) – N (x ₁) и N_Х (α) = P (Х < α), где

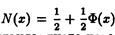, а - функция Лапласа

1. Доверительные интервалы для неизвестного математического ожидания m=E(X) при известной дисперсии σ²= DX

 

Согласно свойству асимптотической нормальности выборочного среднего 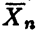имеем 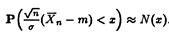, то есть приблизительно равна функции распределения нормального закона.

Тогда для любого z>0

 

 

 

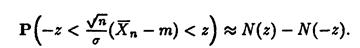
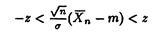эквивалентно где функция распределения нормального закона

 

 

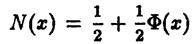выражается через функцию Лапласа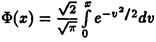

 

 

Получим ввиду нечетности функции Лапласа

 

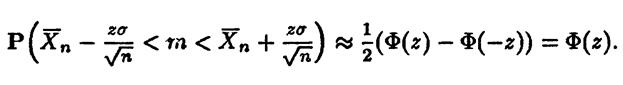
Поскольку, как уже говорилось (Лекция 19) для функции Лапласа существуют таблицы, можно взять в качестве z z_α – ее квантиль порядка α.

 

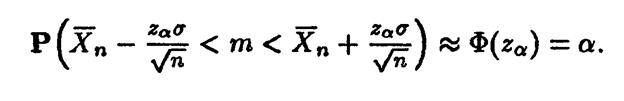
2. Доверительные интервалы для неизвестного математического ожидания m=E(X) при неизвестной дисперсии σ²= DX

Проведя аналогичные рассуждения, можно воспользоваться последней формулой, взяв в качестве σ корень из выборочной дисперсии 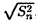, где

 

 

 

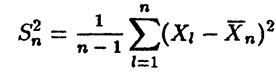
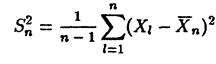
Тогда мы получим аналогичное приближение

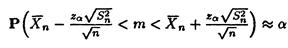
и аналогичный интервал

 

 

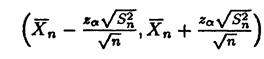
Замечание 24.16

В построениях мы использовали свойство асимптотической нормальности, то есть допущение n→∞. На практике это означает требование большого размера выборки.

 

Если мы будем рассматривать исходную случайную величину с нормальным законом распределения, тогда можно построить доверительный интервал с вероятностью, ровно равной α, поскольку тут нет необходимости в асимптотических формулах и имеет место «удобное» нормальное распределение. Соответственно, n может быть относительно небольшим.

положим

 

В случае, если рассматривается выборка из нормального закона, для построения доверительных интервалов используется Лемма (Теорема) Фишера:

 

Пусть Х₁, Х₂,…..Х_n — независимая выборка из генеральной совокупности с нормальным законом распределения. Пусть 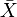— выборочное среднее, а — несмещённая выборочная дисперсия. Тогда

 

1. 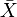и независимы

 

Замечание 24.17. Часто приходится слышать, что «независимые величины – это величины, не имеющие ничего общего». Это убедительный контрпример для подобного заблуждения: выборочное среднее и дисперсия не просто «имеют что-то общее», а вторая выражается через первое.

 

2. имеет стандартное нормальное распределение. Позволяет оценить неизвестное математическое ожидание a при известной дисперсии и наоборот, неизвестную дисперсию σ по известному математическому ожиданию a.

 

Случай, аналогичный предыдущему. Подобрав по заданному α такое d, что P (| 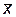– a | < d) = α, получим 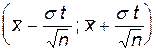= α

 

Задача. Пусть имеется генеральная совокупность с некоторой характеристикой, распределенной по нормальному закону с дисперсией, равной 6,25. Произведена выборка объема n = 27 и получено средневыборочное значение характеристики 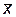= 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с доверительной вероятностью
α =0,99.

Решение. Сначала по таблице для функции Лапласа найдем значение t из равенства F (t) = α / 2 = 0,495. По полученному значению
t = 2,58 определим точность оценки (или половину длины доверительного интервала) d: d=s t / 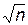= 2,5´2,58 / 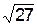» 1,24. Отсюда получаем искомый доверительный интервал: (10,76; 13,24).

 

 

3. 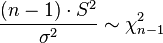то есть имеет распределение «хи-квадрат» с n-1 степенью свободы. Позволяет оценить неизвестную дисперсию при неизвестном математическом ожидании

 

Задача. Будем считать, что шум в кабинах вертолетов одного и того же типа при работающих в определенном режиме двигателях — случайная величина, распределенная по нормальному закону. Было случайным образом выбрано 20 вертолетов, и произведены замеры уровня шума (в децибелах) в каждом из них. Исправленная выборочная дисперсия измерений оказалась равной 22,5. Найти доверительный интервал, накрывающий неизвестное стандартное отклонение величины шума в кабинах вертолетов данного типа с доверительной вероятностью 98%.

Решение. По числу степеней свободы, равному 19, и по вероятности (1 – 0,98)/2 = 0,01 находим из таблицы распределения c ²величину
c ₂² = 36,2. Аналогичным образом при вероятности (1 + 0,98)/2 = 0,99 получаем c ₁² = 7,63. Используя формулу для доверительного интервала, получаем искомый доверительный интервал: (3,44; 7,49).

 

4. 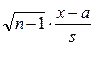~ t _n-1, то есть имеет распределение Стьюдента с n-1 степенью свободы. Позволяет оценить неизвестное математическое ожидание при неизвестной дисперсии. (s – выборочная дисперсия), используя свойство функции распределения закона Стьюдента t (-x) = 1 – t (x)

 

Задача. На контрольных испытаниях 20-ти электроламп средняя продолжительность их работы оказалась равной 2000 часов при среднем квадратическом отклонении (рассчитанном как корень квадратный из исправленной выборочной дисперсии), равном 11-ти часам. Известно, что продолжительность работы лампы является нормально распределенной случайной величиной. Определить с доверительной вероятностью 0,95 доверительный интервал для математического ожидания этой случайной величины.

Решение. Величина 1 – α в данном случае равна 0,05. По таблице распределения Стьюдента, при числе степеней свободы, равном 19, находим: t_α = 2,093. Вычислим теперь точность оценки: 2,093´121/ = 56,6. Отсюда получаем искомый доверительный интервал:

(1943,4; 2056,6).

 

 

Приложение. Распределения c² и Стьюдента

(по курсу лекций А.В.Степанова, МГИМО)

 

Распределение c².

Пусть имеется n независимых случайных величин x₁, x₂,..., x_n, распределенных по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Тогда случайная величина распределена по закону, который называется “распределение c²” или “распределение Пирсона”. Очевидно, что она может принимать лишь неотрицательные значения. Число n называется числом степеней свободы.

При n > 1 график плотности распределения случайной величины c² представляет собой кривую, изображенную на рисунке 1.

Для того, чтобы определить вероятность попадания случайной величины c² в какой-либо промежуток из множества положительных чисел, пользуются таблицей распределения c². Обычно такая таблица позволяет

 

q n	0,99	0,975	0,95	...	0,1	0,05	0,01
	0,0315	0,0398	0,0239	...	2,71	3,84	6,63
...	...	...	...	...	...	...	...
	2,56	3,25	3,94	...	16,0	18,3	23,2
...	...	...	...	...	...	...	...

Таблица 1.

 

по вероятности q и по числу степеней свободы n определить так называемый квантиль c _q ², если q и c _q ² связаны соотношением

P (c² > c _q ²) = q.

Эта формула означает: вероятность того, что случайная величина c² примет значение, большее чем определенное значение c _q ², равна q.

Таблица 1 представляет собой фрагмент таблицы распределения c². Из него видно, что случайная величина c² с 10-ю степенями свободы с вероятностью q = 0,95 принимает значение, большее 3,94, а та же величина с одной степенью свободы с вероятностью q = 0,975 превышает 0,00098.

Задача. Найти интервал (c₁²,c₂²), в который случайная величина c² с 10-ю степенями свободы попадает с вероятностью, равной 0,9.

Решение. График плотности распределения c² с 10-ю степенями свободы схематично изображен на рисунке 2. Будем считать, что площади заштрихованных областей (правая область не ограничена справа) равны между собой. Примем условия:

P (c² < c₁²) = P (c² >c₂²) = (1 - 0,9)/2 = 0,05, (1)

тогда P (c₁² < c² < c₂²) = 0,9.

Равенства (1) сразу позволяют по таблице определить: c₂² = 18,3. Для определения левой границы интересующего нас интервала придется воспользоваться очевидным равенством P (c² > c₁²) = 0,95. Из таблицы 1. определяем: c₁² = 3,94, и теперь можно сформулировать ответ задачи: значение случайной величины c² с вероятностью 0,9 принадлежит интервалу (3,94; 18,3).

Распределение Стьюдента.

Многие задачи статистики приводят к случайной величине вида

,

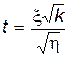где x и h – независимые случайные величины, причем x – нормально распределенная случайная величина с параметрами M x = 0 и D x = 1, а h распределена по закону c² c k степенями свободы.

Закон распределения случайной величины t называется законом распределения Стьюдента с k степенями свободы.

График плотности распределения для закона Стьюдента схематически изображен на рисунке 3. Кривая плотности распре­деления схожа с аналогичной кривой для нормального распределения.

Таблицы распределения Стьюдента позволяют при данном числе степеней свободы k по вероятности q определить значение t_q, для которого выполняется соотношение P (| t | > t_q) = q. Фрагмент такой таблицы представляет собой таблица 2.

 

q k	0,1	0,05	...	0,01	0,005	...
	6,314	12,71	...	63,57		...
...	...	...	...	...	...	...
	1,782	2,179	...	3,055	3,428	...
...	...	...	...	...	...	...
Таблица 2

Задача. Найти симметричный интервал, в который случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы, попадает вероятностью 0,9.

Решение. Очевидны соотношения:

P (– x < t < x) = P (| t | < x) = 1 – P (| t | ³ x) = 0,9.

Из последнего равенства следует:

P (| t | ³ x) = 0,1, (n = 12).

Определяем из таблицы: x = 1,782. Нестрогое неравенство в скобках в левой части последней формулы нас не должно смущать, так как мы имеем дело с непрерывной случайной величиной, и вероятность того, что она примет конкретное значение, равна нулю.

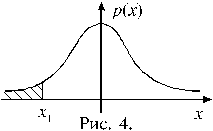
Задача. Найти значение x из условия P (t > x) = 0,995, где t – случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы.

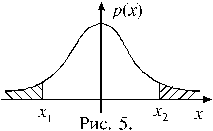
Решение. На рисунке 4 изображен график плотности распределения Стьюдента с 12-ю степенями свободы. Вероятность того, что случайная величина примет значение из области справа от точки x ₁ равна 0,995, следовательно в область левее этой точки случайная величина попадает с вероятностью 0,005. Чтобы найти x ₁, рассмотрим две симметричные области, изображенные на рисунке 5. Допустим, что в каждой из этих областей значение случайной величины оказывается с вероятностью 0,005. Тогда получаем: x ₁= – x,
x ₂ = x, причем x определяется из условия
P (| t | > x) = 0,01. Из таблицы 2 находим: x = 3,055. Теперь можно выписать ответ задачи:

P (t > –3,055) = 0,995.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: