 |
Часть II Теория возмущенного движения
|
|
|
|
ПРОГРАММА ДИСЦИПЛИНЫ
НЕБЕСНАЯ МЕХАНИКА
Цикл - ДС.3
Специальность: 300200 - Астрономогеодезия
Принята на заседании кафедры астрономии и космической геодезии
(протокол № 1 от " 2 " сентября 2008 г.)
Заведующий кафедрой
(Н.А.Сахибуллин)
Утверждена Учебно-методической.комиссией физического факультета КГУ
(протокол № 4__ от "21" сентября 2009 г.)
Председатель комиссии
__________________(Д.А.Таюрский)
Рабочая программа дисциплины «НЕБЕСНАЯ МЕХАНИКА»
| по специальности: 300200 - Астрономогеодезия |
предназначена для студентов 3 курса,
АВТОР: доцент Загретдинов Р.В., доцент Кондратьева Е.Д., доцент Ишмухаметова М.Г.
КРАТКАЯ АННОТАЦИЯ: изучаются законы невозмущенного движения небесных тел и ИСЗ, методы решения уравнений движения тел Солнечной системы и методы определения невозмущенной орбиты, рассматриваются элементы возмущенного движения, определяется понятие силовой функции как в задаче многих тел, так и в ограниченных задачах небесной механики.
1. Требования к уровню подготовки студента, завершившего изучение дисциплины «НЕБЕСНОЙ МЕХАНИКИ»
Студенты, завершившие изучение данной дисциплины должны:
- знать основные законы движения небесных тел, элементы орбиты и диапазон их изменения, методы определения орбит из наблюдений, типы движения планет, спутников, астероидов, комет, основы теории движения ИСЗ;
- уметь вычислять поисковую эфемериду, элементы орбиты по угловым и смешанным наблюдениям, составлять дифференциальные уравнения движения небесных тел и решать их методом численного интегрирования
Объем дисциплины и виды учебной работы (в часах).
Форма обучения: очная
|
|
|
Количество семестров: 1
Форма контроля: 5 семестр - зачет, экзамен
| № п/п | Виды учебных занятий | Количество часов | |
| 5 семестр | 6семестр | ||
| 1. | Всего часов по дисциплине | ||
| 2. | Самостоятельная работа | ||
| 3. | Аудиторных занятий | ||
| в том числе лекций | |||
| семинарских (или лабораторно-практических) |
Содержание дисциплины.
3.1. ТРЕБОВАНИЯ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА К ОБЯЗАТЕЛЬНОМУ МИНИМУМУ СОДЕРЖАНИЯ
ПРОГРАММЫ
| Индекс | Наименование дисциплины и ее основные разделы | Всего часов |
| ДС.3. | небесная механика; дифференциальные уравнения невозмущенного движения ИСЗ; интегрирование дифференциальных уравнений невозмущенного движения; исследование невозмущенного движения; вычисление координат и составляющих скорости по элементам орбиты; определение орбиты по координатам и составляющим скорости; вычисление эфемериды ИСЗ; методы определения предварительных орбит; элементы лагранжевой и гамильтоновой механики; уравнения Лагранжа и Ньютона для оскулирующих элементов орбиты; разложение координат ИСЗ и их функций в ряды; возмущающие функции и возмущающие ускорения, действующие на ИСЗ; точечное представление геопотенциала; возмущения от гравитационного поля Земли, притяжения Луны и Солнца, светового давления, сопротивления атмосферы, электромагнитных сил; резонансные возмущения; вращение ИСЗ относительно собственного центра масс; методы интегрирования уравнений движений небесных тел; системы нелинейных обыкновенных дифференциальных уравнений в задачах астрономии и космической геодезии, общий подход к их интегрированию; приближенные аналитические методы интегрирования нелинейных дифференциальных уравнений в задачах астрономии и космической геодезии; метод последовательных приближений (Пикара); метод малого параметра; методы осреднения; гамильтоновы системы; методы численного интегрирования дифференциальных уравнений в задачах астрономии и космической геодезии; классические многошаговые (конечно-разностные) методы (Адамса, Коуэлла, Штермера); классические одношаговые методы (Рунге-Кутта); современные высокоточные методы численного интегрирования движения небесных тел; проблема периодических решений; задача об устойчивости. |
|
|
|
3.2. СОДЕРЖАНИЕ РАЗДЕЛОВ ДИСЦИПЛИНЫ
| № п/п | Название темы и ее содержание | Количество часов | |
| лекции | семинарские (лаб.-практ.) занятия | ||
| Предмет и задачи небесной механики. Исторический очерк развития небесной механики как науки. Основные этапы и достижения. | |||
| Задача двух тел. Притягивающий и непритягивающий спутники. Постановка задачи и дифференциальные уравнения. Система единиц измерения в небесной механике, постоянная Гаусса. | |||
| Первые интегралы дифференциальных уравнений движения. Интегралы площадей, энергии, Лапласа. Законы Кеплера. | |||
| Типы невозмущенного движения (эллиптическое, параболическое, гиперболическое, круговое, прямолинейное). Астрономический смысл постоянных интегрирования, кеплеровские элементы орбиты, пределы их изменения. | |||
| Уравнение траектории движения небесного тела. Уравнение Кеплера и способы его решения. Основные формулы кругового, эллиптического, параболического и гиперболического движений. | |||
| Эфемерида небесного тела. Вычисление прямо-угольных гелиоцентрических и геоцентрических координат. Переход к экваториальным и эклиптическим гелио- и геоцентрическим координатам. Назначение эфемериды и ее точность. | |||
| Постановка задачи определения элементов невозмущенной орбиты из наблюдений. Методы Лагранжа, Гаусса, Лапласа, Эскобала, по трем угловым наблюдениям, по смешанным данным. Определение приближенной невозмущенной орбиты по двум наблюдениям. | |||
| Принципы и основные этапы улучшения невозмущенных орбит,. Дифференциальный способ улучшения орбит. Разложение координат в ряды по степеням времени, эксцентрической и средней аномалий. | |||
| Решение дифференциальных уравнений методом численного интегрирования. | |||
| Основы астродинамики: невозмущенное движение космических аппаратов и ИСЗ. Скорость спутника, ее компоненты, годограф скорости. Трасса спутника, задачи перехвата и перелета, траектории Гомана. Продолжительность перелета, теорема Ламберта. | |||
| Понятие возмущаемого движения. Возмущающая сила. Действие составляющей возмущающей силы. | |||
| Задачи N – тел в небесной механики. Равнение в абсолютных координатах. Силовая функция и ее свойства. Интегралы уравнений. Работы Брукса, Пуанкаре, Пенлеве. Движение Солнечной системы относительно звезд. Плотность Лапласа. | |||
| Уравнения относительного движения в задаче N – тел. Первая форма уравнений относительного движения. Пертурбационная функция. | |||
| Метод вариации произвольной постоянной. Общая схема метода ВНП. Оскулирующие элементы. Основная операция. Вывод уравнений Эйлера (Ньютона). Уравнение ИСЗ в центральном поле тяготения с учетом сопротивления атмосферы. | |||
| Канонические уравнения в небесной механике и понятие их интегрируемости. Канонические уравнения эллиптического движения. | |||
| Уравнения Лагранжа. Вывод уравнений Лагранжа. Решение уравнений движения планет в форме Лагранжа. Свойства возмущений. Малые делители и понятие резонанса в небесной механике. | |||
| Краткая характеристика теорий движения планет, спутников, астероидов, комет, Луны, ИСЗ. | |||
| Ограниченная задача трех тел. Постановки задачи. Уравнение движения в абсолютных координатах. Вывод уравнений в синодической системе координат. | |||
| Итого часов: |
|
|
|
3.3. СОДЕРЖАНИЕ ЛЕКЦИЙ, СЕМИНАРСКИХ, ЛАБОРАТОРНО-ПРАКТИЧЕСКИХ ЗАНЯТИЙ И САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Часть II Теория возмущенного движения
| Тема 1 | Понятие возмущенного движения. Введение |
| Лекция 1 | Понятие возмущаемого движения. Возмущающая сила. Действие составляющей возмущающей силы. |
| Тема 2 | Задача N – тел в небесной механики. |
| Лекция 2 | Равнение в абсолютных координатах. Силовая функция и ее свойства. Интегралы уравнений. Работы Брукса, Пуанкаре, Пенлеве. Движение Солнечной системы относительно звезд. Плотность Лапласа. |
| Лекция 3 | Уравнения относительного движения в задаче N – тел. Первая форма уравнений относительного движения. Пертурбационная функция. |
| Тема 3 | Метод вариации произвольной постоянной. |
| Лекция 3 | Общая схема метода ВНП. Оскулирующие элементы. Основная операция. |
| Лекция 4 | Вывод уравнений Эйлера (Ньютона). |
| Лекция 5 | Уравнение ИСЗ в центральном поле тяготения с учетом сопротивления атмосферы. Канонические уравнения в небесной механике и понятие их интегрируемости. |
| Лекция 6 | Канонические уравнения эллиптического движения. |
| Лекция 7 | Уравнения Лагранжа. Вывод уравнений Лагранжа. Решение уравнений движения планет в форме Лагранжа. Свойства возмущений. Малые делители и понятие резонанса в небесной механике. |
| Лекция 8 | Открытие планеты Нептун. Краткая характеристика теорий движения планет, спутников, астероидов, комет, Луны, ИСЗ. |
| Тема 4 | Ограниченная задача трех тел. |
| Лекция 9 | Постановки задачи. Уравнение движения в абсолютных координатах. Вывод уравнений в синодической системе координат. Интеграл Якоби. |
| Лекция 10 | Области допустимого движения в ограниченной задаче трех тел. Сферы Роша. |
| Лекция 11 | Точки либрации. Движение в окрестности точек либрации. |
|
|
|
ОСНОВНАЯ ЛИТЕРАТУРА
1. Г.Н. Дубошин. Небесная механика. Основные задачи и методы. 1975.
2. М.Ф. Субботин. Введение в теоретическую астрономию. 1968.
3. Р.Ф. Аппазов, О.Г.Сытин. Методы проектирования траекторий носителей и спутников Земли. 1987.
4. К.В.Холшевников, В.Б.Титов. Задача двух тел.- С-Пб. 2007. 179с.
5. К.Мюррей, С.Дермотт. Динамика солнечной системы. М.Физматлит. 2009. 588с.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. А.Д.Дубяго. Определение орбит. 1949
2. М.Б.Балк. Элементы динамики космического полета. 1965
3. М.Г.Ишмухметова, Е.Д.Кондратьева. Методы астродинамики. Часть 1. Методическое пособие. КГУ. 2001.
4. М.Г.Ишмухметова. Методы астродинамики. Часть 2. Методическое пособие. КГУ. 2003.
5. М.Г.Ишмухметова, Е.Д.Кондратьева. Решение задач по небесной механике и астродинамике. Учебно-методическое пособие. КГУ. 2009.
«НЕБЕСНАЯ МЕХАНИКА»
ЗАДАНИЯ К ЗАЧЕТУ
1. Решение задач на нахождение параметров движения спутников в невозмущенном движении в задаче двух тел.
2. Вычисление эфемериды движущегося небесного тела по известным элементам их орбит.
3. Определение предварительной орбиты по нескольким наблюденным положениям спутника одним из предложенных методом.
|
|
|
БИЛЕТЫ К ЭКЗАМЕНУ
Билет № 1
1) Задача двух тел. общая постановка, основные уравнения движения.
2) Ограниченная задача 3-х тел. Области движения.
Билет № 4
1) Интеграл площадей. Три формы интеграла площадей (векторная, координатная и полярная)
2) Ограниченная задача 3-х тел. Движение в окрестности точек либрации.
Билет № 6
1) Задача 2-х тел. Интегралы Лапласа.
2) Задача n – тел. Постановка задачи, уравнения движения в абсолютных координатах. Силовая функция и её свойства.
Билет №7
1) Астрономическая интерпретация постоянных интегрирования.
2) Задача n – тел. Интегралы уравнений. Результаты Брунса, Пуанкаре и Пенлеве.
Билет № 8
1) Кеплеровские элементы орбиты, их назначение, границы изменения.
2) Движение солнечной системы относительно звёзд.
Билет № 9
1) Законы Кеплера. Уравнение Кеплера.
2) Плоскость Лапласа.
Билет № 10
1) Интеграл энергии и форма орбиты тела.
2) Уравнение Эйлера (Ньютона). Вывод для 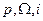
Билет № 11
1) Истиная, эксцентрическая и средняя аномалия. Постоянная Гаусса.
2) Действия составляющих возмущающей силы (геометрическая интерпретация).
Билет № 12
1) Вычисление r и v по элементам орбиты, плоская задача.
2) Понятие о возмущающей силе.
Билет № 13
1) Вычисление прямоугольных координт тела в пространстве.
2) Уравнения Эйлера (Ньютона), вывод для a и e.
Билет № 14
1) Переход от эклиптических гелиоцентрических к экваториальным гелиоцентрическим, экваториальным геоцентрическим и к экваториальным геоцентрическим сферическим координатам.
2) Движение ИСЗ в нецентральном поле тяготения.
Билет № 15
1) Эфемерида. Постановка задачи, основные уравнения.
2) Уравнения движения ИСЗ с учётом сопротивления атмосферы.
Билет № 16
1) Разложение координат в ряды по степеням времени.
2) Решение уравнения движения планет в форме Лагранжа. Свойства возмущений.
Билет № 17
1) Метод Лагранжа определение элементов орбиты тела. Постановка задачи, ход решения.
2) Задача n – тел. Первая форма уравнений относительного движения. Пертурбационная функция.
Билет № 18
1) Основное уравнение метода Лагранжа (определение элементов орбиты тела) и возможность его решения, исключительные случаи.
2) Ограниченная задача 3–х тел. Интеграл Якоби.
Билет № 19
1) Метод Гаусса вычисления отношения площади сектора к площади треугольника.
2) Малые знаменатели и резонансы.
Билет № 20
1) Определение элементов орбиты тела по его координатам на два момента.
2) Метод вариации произвольной постоянной. Общая схема.
Билет № 24
1) Оскулирующие элементы. Основная операция.
2) Ограниченная задача 3-х тел. Вывод уравнения задачи в синодической системе координат.
Билет № 25
1) Улучшение орбит тел по многим наблюдениям (принцип).
2) Ограниченная задача 3-х тел. Постановка задачи. Уравнения движения в абсолютных координатах.
|
|
|


