Главная | Обратная связь | Поможем написать вашу работу!

Связи между элементами

Информация и информационные процессы.

Определение понятия информации

Информация по-латыни означает сообщение.

Определения информации.

1. Информация ¾ сведения, не зависящие от формы их представления.

2. Информация ¾ знание, то есть позволяющая получившему их совершать целенаправленное действие.

3. Информация по Шеннону. Информация¾ сообщение, которое уменьшает или устраняет неопределённость в выборе одной возможности из нескольких.

4. Информация ¾ мера сложности структур.

Читатель

Преобраз. базы знаний Принятие решения не свя- занного с обр. знания

Преобразование ие

Знания

Информация

Анализ

Приём

Понятие данные

Данные ¾ информация, выраженная в формализованном виде, обеспечивающая возможность хранения, обработки и передачи.

Документ ¾ данные, представленные на определённом носителе и обладающие определённой структурой.

Строго определённая структура документа упрощает работу с ним.

Пример:

паспорт, железнодорожный билет.

Его строго определённая форма затрудняет его подделку (деньги).

Элементы документа:

1. Указано название и его назначение

2. Реквизиты исполнителя документа.

Информационные процессы

Независимо от способа получения и хранения информация имеет единые характеристики. Информация наряду с веществом и энергией считается сейчас фундаментальным понятием.

В этом смысле информация это структура окружающего нас мира, способная влиять на процессы.

Учёные установили, что геометрическая структура обладает возможностью влиять на психику человека, воздействуя на его подсознание.

Свойства информации:

1.Информация может накапливаться.

2.Информация не обладает свойством сохранения.

3.Информация может самоорганизовываться, порождая новую информацию.

Информационное общество

Это общество, в котором большинство трудоспособного населения занято производством, хранением, передачей, преобразованием и использованием информации.

США, страны западной Европы и Японии уже вступили в фазу информационного общества, а Россия ещё нет.

Низкая производительность Низкое развитие информационных

труда и в сельском хозяйстве. структур.

Язык как способность представления информации.

Кодирование информации.

Структура информации, составленная из элементов. Текстовая информация ¾ буква. Устная информация ¾ звук (фонема).

Географическая информация (изображением в качестве элементов является контур, цветовое пятно, элементарная форма и т. д.).

Признак элемента информации

Дорожные знаки и сигналы. Азбука глухонемых (элементом является жест).

Связи между элементами

1. Иерархическая.

РАМУ

МАМА

МЫЛА

МАМА МЫЛА РАМУ

ФФФФ

2. Линейная ¾ связь букв в слове и слов в предложении.

МАМА МЫЛА РАМУ

М А М А

Сетевая.

Достоинство сетевой структура является высокая скорость взаимодействия элементов (интернет). Сетевые структуры очень устойчивы к повреждениям связи, так как при разрыве связи соединение осуществляется в обход. Недостаток сетевой структуры заключается в том, что необходимо иметь большое количество связи.

Языки

Естественные Искусственные (код)

Процесс записи на искусственном языке называется кодированием, а обратный процесс декодированием.

СПАСИТЕ НАС! кодирование SOS декодирование СПАСИТЕ НАС!

Применение искусственных языков или кодов:

1. Азбука Морзе.

2. Телеграфный код.

3. Жаргон (арго), воровской жаргон.

Специальный или профессиональный жаргон ¾ естественный язык, образованный естественным путём и в отличии от искусственного языка сам изменяется или развивается. Любой язык, как естественный, так и искусственный состоит из множества элементов (алфавита) и множества правил составления из множества элементов осмысленных сообщений (синтаксис).

Двоичная форма представления информации.

Двоичная форма представления информации заключается в том, что она координируется двумя символами:0 и 1 т. е. да (1) и нет (0). Любую информацию можно представить как результат ответов на вопросы да или нет. В том случае если вариантов больше чем два их множество делят пополам, и ответ заключается в том, находятся в этой части правильный ответ. Такой способ называется дихотомия. Пример: я хочу определить в каком месяце у человека день рождения, задавая ему вопросы, на которые он будет давать ответы да или нет. Все месяца мы пронумеруем:

1,2,3,4,5,6,7,8,9,10,11,12

День рождения

5,6

4,5,6..

1,2,3.

Двоичная система записи чисел:

123=100+20+3

102*1+2*101+ 3*100

3127=3000+100+20+7

an*10n +an-1*10n-1+…..a1*101+a0*100

an*2n+an-1*2n-1+…..a1*21+a0*20

2в ст.0=1 2в ст.4=16

2в ст.1=2 2в ст.5=32

2в ст.2=4 2в ст.6=64

2в ст.3=8 2в ст.7=128 и т.д.

0 1 2 3 4 5 6 7 8 9 10 11 12 13…

02=010

12=110

102=210

112=310

1002=410

1012=510

1102=610

1112=710

10002=810

10012=910

10102=1010

10112=1110

11002=1210

Количество и единицы измерения информации.

Подход к определению количества информации статистический. Согласно ему количество информации определяется как количество элементов. Пример:

1. Книга содержит 300000 знаков (буквы, знаки препинания, цифры, пробелы и т. д.). Журнал же содержит 5000 знаков, т. е. там, где больше элементов, там же и больше информации.

2. Я заказал телефонный разговор с другим городом на 5 минут, а другой человек заказал разговор на 15 минут. Кто может больше передать информации?

3. Небольшая картина и огромное живописное полотно (бородинская панорама) и т. д.

Статистический способ определения количества информации применяется при организации её передачи, хранения, преобразования или уничтожения. Статистический способ, измеряя информацию, не учитывает её смысл. Пример:

1. Определите количество информации в этой фразе (43 байта)

2. Определение количества информации вероятный. Единица информации при этом является бит. Один бит информации содержится в ответе да или нет, если оба варианты ответов равновероятны. Пример:

При подбрасывании монетки ответ на вопрос, какой стороной она упала, содержит 1 бит. Если число возможных исходов больше двух, то количество информации можно определить методом дихотомии. Пример определения количества информации при выборе карты из колоды. Пронумеруем карты.

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36 1бит

В этом примере приблизительно 5,5 бит информации. Пример:

Определите методом дихотомии, сколько информации содержится в ответе на вопрос: «Какая масть выпадет при случайном вытаскивании карты из колоды.»

Пример: определите количество информации, содержащиеся в ответе на вопрос: «Какое число выпало при бросании игральной кости.»

1бит 1бит т. е. 2 бита

4,5,6

4,5

1,2,3,4,5,6

1,2,3

Единица знака¾байт=8 битам. Пример: Определите, сколько байт содержится в ответе на предыдущий пример. 2 байта.

Сколько байт содержится в фразе, написанной ранее. 168 байт. Более крупные единицы называются Кбайты. 1Кбайт=1024 байта, дальше Мбайт¾1024 Кбайт, дальше Гбайт¾1024 Мбайт, дальше Тбайт¾ 1024 Гбайт. Средний персональный компьютер хранит в себе около 10 Гбайт. Одна дискета может хранить 1,5 Мбайта, CD диск имеет ёмкость около 700 Мбайт

Измерение количества графической информации.

10000000001

На экране монитора изображение составлено по горизонтали из 800 точек,

по вертикали из 640 строк. Всего точек 480000, каждая из которых записывается числом, обозначающим её цвет. Максимальное количество цветов, которое может содержать компьютер составляет 16,7 миллиона. Это позволяет воспроизводить на экране компьютера естественные цвета. Точечный способ записи изображения позволяет хранить и воспроизводить любые изображения, но имеет недостатки:

1. Изображение при увеличении или деформации становится зернистым.

2. Такое изображение занимает в памяти компьютера очень большой объём.

Векторный способ хранения изображения заключается в том, что изображение описывается математическими формулами. Сама формула занимает мало места в памяти компьютера, и при запуске соответствующие программы преобразовывают эту формулу в изображение. Этот способ имеет следующие достоинства:

1. Очень экономичен.

2. При изменении параметров картинка будет меняться, т. е. каждая формула содержит не одну, а сотни картинок, что позволяет создавать двигающиеся изображение. Недостатком векторного способа является сложность некоторых формул для построения фотореалистичного изображения. Пример: рекламное изображение всё-таки до сих пор не создают полного эф

3. фекта реальности и больше похожи на мультипликацию, но развивающиеся компьютерные технологии очень скоро приведут к тому, что эти изображения будут полностью неотличимы от реальных. Это позволит создавать кинофильмы на компьютере.

Основные понятия и операции формальной логики.

Логика¾наука, которая с помощью формальных правил определяет истинность или ложность высказывания. При создании компьютеров его элементы получили название логических элементов.

Элементарные логические функции.

Это функции, которые могут принимать значение 0 или 1. Из трёх и, или, не. Наиболее просто смысл логических функций объясняется с помощью электронной системы выключателя. Функция И

1вкл.	2 вкл

88П 88

Функция ИЛИ

Функция НЕ

Помимо простых функций И, ИЛИ, НЕ существуют ещё так называемые сложные функции, то есть сочетание простых функций И, ИЛИ, НЕ.

Логические элементы компьютера.

Компьютер состоит из миллионов элементов, связанных между собой и взаимодействующих во время его работы. Каждый элемент выполняет какую-либо операцию над двоичным разрядом.

Машинные элементы делятся на логические, запоминающие и вспомогательные. Из логических элементов состоят операционные схемы, обеспечивающих выполнение арифметических и логических операций над цепочками двоичных разрядов¾машинными символами. Запоминающие элементы предназначаются для хранения информации. Вспомогательные элементы предназначаются для формирования стандартных сигналов и согласования работы операционных схем.

Переменные и функции, принимающие значение 0 или 1 носят название логических или булевских по имени английского математика и логика Джорджа Буля (1815-1864), является создателем современной символической логики. Подробным изучением булевских функций занимается область математической логики или исчислением высказываний. Каждому высказыванию в соответствии значение её функции, истинности, равное 1, когда высказывание истинно и 0, когда оно ложно.

Логическая функция И.

Логическая функция И от двух аргументов определяется таблицей.

Этим значением

обозначается

Конъюнкция

Легко видеть, что логическая функция И совпадает с произведением аргументов. Поэтому её называют также логическим умножением. Ещё одно название¾Конъюнкция. Нетрудно определить функцию И для любого конечного числа аргументов. Она равна 1 тогда и только тогда, когда все сомножители равны 1, как и должно быть для произведения. Логическое умножение подчиняется переместительному и сочетательному законам.

-2+3=3+2 Коммутативны 7-3=3-7 Не коммутативны

7*3=3*7

(3+2)+7=3+(2+7)

5+7=3+9

(3*7)*2=3*(7*2)

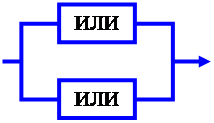
Логическая функция ИЛИ

Логическая функция ИЛИ от двух аргументов определяется таблицей. Её называют логическим сложением или Дизъюнкцией. Следует помнить, что логическая сумма отличается от арифметической суммы. Логическая сумма нескольких слагаемых ровна 0 тогда и только тогда, когда все слагаемые равны 0. Эта операция также подчиняется переместительному и сочетательному законам.

Дизъюнкция

Логическая функция НЕ.

Логическая функция НЕ (отрицание) зависит от одного аргумента и определяется таблицей. Функция НЕ обозначается горизонтальной чертой над аргументом или особым знаком.

Логические выражения и их образование.

Подобно арифметическим операциям, логические операции имеют различное «Старшинство», что отражается на порядке их выполнения в выражениях, содержащих символы различных операций: прежде всего выполняются операции НЕ, затем И и только потом ИЛИ. Здесь наблюдается полная аналогия с алгебраическими выражениями. При вычислении по формуле а2*b2+c2 сначала выполняется возведение в степень, затем умножение и тол ько потом сложение аналогично формуле.

Сначала выполняются отрицания, затем конъюнкция, а потом дизъюнкция. В тех случаях, когда нужно изменить этот порядок применяются круглые скобки. Правила их применения ничем не отличаются от правил применения скобок в алгебраической формуле.

Логические выражения и их преобразование.

Любую функцию трёх и более аргументов можно представить формулой, в которой в которой фигурируют элементарные логические функции. Например, функция три аргумента представленная таблицей.

Аргументы	Функ.
а	b	c	z






1

Преобразование информации.

Преобразованием или перекодированием информации называют её запись с помощью других знаков. Пример:

Перевести с одного языка на другой, записать устную речь, чтение вслух, описание словами какого-либо рисунка, экранизации романа и др. Проблема, которая при этом возникает:

Иногда происходит потеря части информации из-за несоответствия кодов (при переводе с русского языка на английский невозможна точность перевода из-за отсутствия эквивалентов, т. е. в русском языке есть слова непереводимые на английский).

Наиболее точное преобразование информации происходит при перекодирование на уровне элементов информации. Например, азбука Морзе, в которой каждому знаку соответствует сочетание точек и тире. На таком принципе построено применение телеграфных кодов, кодировка в компьютере. Для того, чтобы унифицировать (сделать) одинаковое кодирование на всех компьютерах была принята таблица кодов ASCLL-код. Пример:

ASCLL-код ¾ буква А-41, а-61, О-30, 1-31.

Всего возможно закодировать 256 разных символов. Можно ввести любой из этих символов, даже если его нет на клавиатуре, нажав на клавишу ALT и удерживая её набрать на числовой клавиатуре ASCLL –код символа.

Шифрование.

Шифрование это частный случай кодирования, при котором обеспечивается невозможность прочтения информации теми, кто не владеет ключом к расшифровке. Шифровать можно как текстовую, так и любую другую информацию, т. е. изображение, звук, видео. Шифруют специальную военную информацию, государственную информацию, коммерческую информацию, а также частную.

Способы шифрования:

1. Шифрование текстовой информации способом сдвига алфавита. Его ещё называют способом Юлия Цезаря.

а б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ь ы ъ э ю я

Информатика ¾ шифрование сдвигом на три знака вперёд. Т. е. слово «информатика» можно зашифровать как «ярчсупгхинг».

Такой способ имеет недостаток, так как сообщение легко расшифровать. Для этого нужно попробовать зашифровать это сообщение, сдвигая алфавит

на 1,2,3 и т. д. буквы. Максимальный сдвиг определяется количеством букв в алфавите. Одно из таких сообщений обязательно будет расшифровкой.

2. Для того, чтобы сообщение было труднее расшифровать применяют шифрование с применением сдвига. Смысл его такой: опять пишут алфавит, а под ним против каждой буквы пишут другую букву в произвольном порядке, так, чтобы разным буквам соответствовали разные буквы.

а б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ь ы ъ э ю я

ж й м б с п г з д л т н ё в и ц ю а к э х ч у р ъ о я щ е ы ф ш ь

Информатика ¾ личуавжэлнж.

Такой способ значительно надёжнее, но и его можно расшифровать. Если составить таблицу процентного состава каждой буквы в зашифрованном сообщении, а затем сопоставить её с таблицей распространённости букв различных текстов, то можно вычислить какое-то количество букв, а затем расшифровать всё сообщение. Угадав ключ один раз можно в дальнейшем расшифровывать все сообщения без проблем. Для борьбы с этим можно применить частую замену ключа.

3. Существует ещё один способ шифрования. Его разновидностью в древности являлся способ палочки и ремешка и способ пластинки с отверстием.

Смоделировать этот способ можно следующим образом:

Запишите сообщение: Сегодня 26 января.

Теперь к каждой букве подставим цифру: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

Сейчас перемешаем эти цифры: 7 12 3 5 8 16 1 4 18 9 10 14 6 11 13 15 17 2

Получаем зашифрованное сообщение: яягд рсо.26вы наяс

Такие сообщения расшифровать очень трудно. Надо перебрать много сотен сочетаний только для того чтобы расшифровать хотя бы одну букву. Так как буквы в компьютере представляются цифрами, а также любая информация представляется цифрами, можно зашифровать не только тексты, но и изображения, а также звуки. Нужно только представить каждую точку изображения или каждый звук

Воспользуйтесь поиском по сайту: