 |
Задачи к зачету по функциональному анализу
|
|
|
|
ВМиК МГУ, 4 курс, 3 поток, зимняя сессия
[1]. А.Н. Колмогоров, С.В.Фомин. Элементы теории функций и функционального анализа.
[2]. А.А.Кириллов, А.Д.Гвишиани. Теоремы и задачи функционального анализа.
[3]. Б. Гелбаум, Дж. Олмстед. Контрпримеры в анализе.
Задача 41. Доказать, что множество непрерывно дифференцируемых на [0;1] функций x(t) таких, что 
, 
где K1,K2 > 0 – постоянные, компактно в пространстве C[0;1].
Указание. Согласно теореме Арцела-Асколи, для предкомпактности семейства функций MÌС[a;b] Û равностепенная непрерывность и равномерная ограниченность этого семейства. Если предкомпактное множество замкнуто, то оно компактно.
Задача 42. Будет ли компактным множество всех степеней xn (nÎ N) в пространстве C[0;1].
Ответ. Нет.
Решение. Из последовательности элементов любого полного компакта можно выделить сходящуюся в нем подпоследовательность. Но любая бесконечная подпоследовательность из { xn } сходится к разрывной функции f(x) = {1, if x = 1; 0 otherwise}.
Задача 43. Доказать, что не всякое ограниченное множество в метрическом пространстве вполне ограничено.
Указание. Единичная сфера S в пространстве l2 ограничена. Рассмотрим точки вида ek (где на k-ом месте в последовательности стоит 1, а на остальных - 0). Расстояние между любыми двумя различными точками em и en равно 
Þ для e < 
в S не существует конечной e-сети (в каждом шаре радиуса e с центром в узле такой e-сети будет лежать не более одной точки ek).
Задача 44. Доказать, что в конечномерном пространстве всякое ограниченное множество относительно компактно.
Указание. В конечномерном пространстве компактность означает замкнутость и ограниченность, поэтому замыкание всякого ограниченного множества компактно.
|
|
|
Задача 45. Доказать, что следующие функционалы в пространстве C[-1;1] являются линейными и непрерывными; найти их нормы.
а) 
Указание. Любой функционал вида g[x;t0] = x (t0), очевидно, является линейным и непрерывным. f(x) является линейной комбинацией таких функционалов. || g[x;t0] || º 1. || f | | = 2/3.
б) 
Указание. Линейность следует из линейности интеграла Римана I(x;[a;b]). Функционал вида I(x;[a;b]) ограничен и имеет норму (b-a). || f || = 2
в) 
Указание. Любой функционал вида J(x;y0;[a;b]) = 
линеен по x и ограничен. || J || = 
. Таким образом, || f || = 1.
Задача 46. Пусть X – множество функций f(x), определенных на всей вещественной прямой, каждая из которых равна нулю вне некоторого конечного интервала. Введем норму, полагая 
. Будет ли пространство X банаховым?
Ответ. Нет.
Указание. Докажем, что пространство X не будет полным. Рассмотрим последовательность функций fn(x) = { exp(- x2), если |x|£n; 0, если |x|>n}. Очевидно, что эта последовательность фундаметальна, но сходится к функции f(x) = exp(- x2) ÏX.
Задача 47. Является ли пространство непрерывных на отрезке [0;1] функций гильбертовым пространством, если скалярное произведение задается следующим образом: 
?
Ответ. Нет.
Указание. Если предположить, что C[0;1] с заданным таким образом скалярным произведением есть гильбертово, то имеем подпространство в гильбертовом пространстве L2[0;1]. Можно подобрать последовательность непрерывных функций { fn } из L2, сходящуюся к разрывной функции f(x) = {0, if x £ 1/2, 1, otherwise). Таким образом, подпространство C[0;1] не полно Þ противоречие.
Задача 48. Показать, что если в гильбертовом пространстве H последовательность x n слабо сходится к x и || xn ||®|| x ||, то последовательность 
сходится сильно, т.е. ||xn - x|| ® 0.
Указание. Предположим, что H сепарабельно. Тогда оно изоморфно пространству l2. Поэтому достаточно доказать это утверждение для пространства l2. Действительно, ||xn - x||2=(xn-x,xn-x)=||xn||2+||x||2-2(x,xn)= ||xn||2-||x||2+2(x,x-xn)®0 (т.к. согласно слабой сходимости, (x,xn-x) ®0).
|
|
|
Задача 49. Доказать, что любой линейный непрерывный функционал в гильбертовом пространстве H достигает нормы на замкнутом единичном шаре.
Указание. Считаем, что пространство H сепарабельно. Функционал F(x)=(a,x) достигает нормы ||F||=||a|| на элементе a/||a||.
Задача 50. Найти норму оператора A, действующего в пространстве C[0;1], (или в пространстве L2[0;1]): 
.
Ответ. ||A|| = sup {||Ax|| (||x|| £ 1)} = 1.
Задача 51. Определить оператор A* и нормы операторов A и A*, если A: l2 ® l2, где A(x1,…,xn,…)= A(0,x1,…,xn,…).
Указание. Сопряженным к l2 является пространство функционалов вида G(x)=(g,x), где gÎ l2. Нужно подобрать оператор A* на множестве таких функционалов, такой что (g,Ax)=(A*g,x). Для функционала G(x)=(g,x), где g=(g1,g2,…,gn,…) положим A*G(x)=G'(x)=(g',x), где g'=(g2,g3,…., gn,…). Поскольку А переводит единичный шар в единичный шар, то ||A|| = 1. Поскольку оператор А ограничен и пространство l2 банахово, то ||A*|| = ||A|| = 1.
Задача 52. Определить спектр оператора A, действующего в пространстве l2: 
.
Ответ. s(A) = {0} È {ln=1/n, nÎ N }.
Указание. Оператор A компактен, поэтому его спектр состоит из нуля и собственных значений. Числа ln являются собственными значениями, т.к. Ker(A-lnI)¹{0}.
Задача 53. В пространстве С[0;1] задан оператор A. Будет ли оператор A компактным?
а) Ax(t) = tx(t).
Ответ. Нет.
Указание. На подпространстве L = { f | f(x) =0 при x£1/2}ÌС[0;1] оператор обратим. Но в бесконечномерном нормированном пространстве компактный оператор не имеет обратного.
б)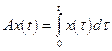 
Ответ. Да.
Указание. A - частный случай компактного оператора Вольтерра.
в) Ax(t)=x(0)+tx(1)
Ответ. Да.
Указание. Подпространство Im(A) конечномерно, образ единичного шара ограничен.
Задача 54. В пространстве 
задан оператор A: 
. Доказать, что оператор A компактен, найти его спектр.
Ответ. s(A) = {0}.
Указание. Оператор А компактен, т.к. является композицией компактного оператора из задачи 52 и ограниченного оператора (сдвига). Поскольку оператор задан в гильбертовом пространстве и компактен, то число 0 входит в его спектр. Легко показать, что собственных значений у оператора нет: из (A-lI) x = 0, l¹0 следует x = 0.
Задача 55. Привести пример линейного, но не непрерывного функционала.
Пример. Пространство {Pi(x)} всевозможных многочленов над R. Норма: ||P||=max(|P(x)|) на отрезке [0;1/2]. Функционал f(P) = P(1). Функционал f не является непрерывным. В самом деле, рассмотрим последовательность Pn=xn. Очевидно, что ||Pn|| ® 0, но f(Pn)®¥.
|
|
|
|
|
|
