Расчет зон касания и коэффициента трения колонны штанг о трубы

Для расчета размера участков прилегания штанг к НКТ будем считать, что все муфты касаются НКТ, и рассмотрим равновесие одной штанги. Тогда прилегающий участок, если он имеется, заключен с обеих сторон провисающими участками, простирающимися от прилегающего участка до муфт (рис. 21). Прогиб штанг внутри НКТ зависит, вообще говоря, от жесткости на изгиб штанг и муфтовых соединений. Эксперимент показал, что жесткость соединения штанг не меньше жесткости тела штанг. Предположим также, что на протяжении одной штанги можно пренебречь изменением эффективной продольной силы Т_е и удельной силы прижатия и отклонение силы штанги совпадает с направлением силы N. Кроме того, пренебрегаем различием жесткости по' длине штанги. В этих предположениях уравнение провисающей части штанги имеет вид [10]

(33)

где X (S) - отклонение оси штанги от оси НКТ; Е - модуль упругости стали; I - момент инерции поперечного сечения штанги.

Будем отсчитывать длину штанги S от муфтового соединения и обозначим длину провисающего участка l (см. рис. 21). Граничные условия имеют вид

Рис- 21. Насосная штанга в искривленном участ­ке ствола скважины

(34)

где h₀ и h₁ - средний зазор между НКТ и соответственно штангами и муфтами; D_т - внутренний диаметр НКТ; D _ш - диа­метр штанг; D_м - диаметр муфт. Можно получить [11]:

(35)

где Т_e = Т + Р*F_ш - эффективная продольная сила; Т - внутрен­няя сила; Р - гидростатическое давление; F_ш - площадь по­перечного сечения штанги; λ = 1 – (γ_ж / γ_ст) (γ_ж - удельный вес жидкости; γ_ж - удельный вес стали); α, φ - соответственно зенитный и азимутальный угол оси скважины.

Предполагается, что ось НКТ совпадает с осью скважины. Штрих.означает производную по длине дуги оси скважины S.

Прижимающая сила складывается (геометрически) из эйле­ровой силы прижатия штанги к искривленной поверхности НКТ Т_e / R и нормальной составляющей веса штанг с учетом архиме­довой силы λ*q*sinα.

Выражение для прижимающей силы упрощается в двух крайних случаях, когда составляющая силы тяжести значительно больше эйлеровой силы и значительно меньше нее.

 

(36), (37)

где R - радиус кривизны оси скважины.

(38)

 

В случае растяжения колонны при Т_e > 0 из решения задачи (33) и (34) получаем уравнение для длины провисающего участка

(39)

Роль жесткости колонны при изгибе определяется значением величины . При большой жесткости или малом натяжении, когда Z «1, имеем Ф(Z) = Z⁴ / 72, и из формулы (39) получаем

(40)

где l _ш - длина штанги.

Из условия касаний штанги находим

Для штанг l _ш = 8 м, D_ш - 22 мм, D_м = 46 мм, q ≈ 30 Н/м, EI – 2*10³Н*м² получаем, что штанга может прилегать к НКТ при N > 6,7 Н/м.

Такая прижимающая сила за счет собственного веса штанг возникает при угле наклона скважины более 13⁰. Натяжение штанг мало в нижней части колонны при ходе вниз, и поэтому при большом наклоне скважины расчет зоны провисания можно производить по формуле (40). Однако в большинстве случаев пренебрегать растягивающей силой нельзя.

При большом натяжении, когда Z» 1, Ф(Z) = Z²/2. Из выра­жения (39) находим

(41)

Формула (41) определяет длину провисающей части штанги, когда можно пренебречь ее жесткостью на изгиб. Подставив (41) в неравенство Z» 1, получим условие справедливости в виде

(42)

Проверим условие (42) в двух крайних случаях (36) и (37), В

случае (36) для рассмотренных выше штанг диаметром 22 мм из (42) находим Т_е» 10³ H. В случае (37) при наименьшем радиусе кривизны R = 100 м также получаем Т_с» 10³ Н.

Следовательно, для расчета отклонения штанг внутри труб можно пренебречь их жесткостью при изгибе, если растяги­вающая сила равна весу нескольких десятков метров штанг. Следует отметить, что при движении колонны вверх уже на плунжер действует значительно большая нагрузка. Поэтому для расчета длины провисающей части штанг будем пользоваться формулой (42). При этом длина прилегающей части, т.е. учас­ток трения, определяется с некоторым избытком.

Полученное решение соответствует провисанию тяжелой нити внутри труб. Для отклонения оси штанг имеем

Если штанга не касается НКТ, то

Введем обозначение

(43)

 

В случае β ≥ 1 штанга полностью провисает, а при β < 1 эта величина определяет долю длины провисающей части штанг

Условие провисания β > 1 в случае, когда можно пренебречь силой тяжести, сводится к геометрическому условию

 

В случае сжатия Т_е < 0 гибкая штанга вся прилегает к НКТ и будем считать β = 0.

Для сосредоточенной силы, с которой муфта прижимается к НКТ при β = 1, можно найти

Учитывая (41) и (43), получаем

(44)

 

Предполагая, что эта сила равномерно распределена по длине муфты, получаем давление муфты на стенку НКТ

(45)

Для силы трения на единицу длины колонны штанг с муфтами

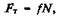(46)

 

где коэффициент трения определяется выражением

(47)

 

Для прижимающих сил штанг Р_ш и муфт Р_м имеем

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: