Омский государственный университет путей сообщения

___________________

 

И. И. Гончар, Н. А. Пономаренко

 

 

Методические указания к решению задач

при изучении разделов физики

«МОЛЕКУЛЯРНАЯ ФИЗИКА», «ТЕРМОДИНАМИКА»

 

Утверждено редакционно-издательским советом университета

 

 

Омск 2007

УДК 530.1(075.8)

ББК 22.34+22.314+22.336

Г65

 

 

Методические указания к решению задач при изучении разделов физики «Молекулярная физика», «Термодинамика» / И. И. Гончар, Н. А. Пономаренко; Омский гос. ун-т путей сообщения. Омск, 2007. 31 с.

 

 

Указания содержат основные формулы молекулярной физики и термодинамики с краткими теоретическими пояснениями, а также примеры решения задач с подробным анализом и задачи для проведения практических занятий, и выполнения индивидуальных заданий и контрольных работ. Цель указаний – выработать у студентов практические умения и навыки в использовании основных понятий и законов молекулярной физики и термодинамики. Все задачи разбиты на шесть тем, к каждой из которых приведены краткие методические рекомендации и теоретический материал.

Предназначены для студентов второго курса технических вузов очной и заочной форм обучения.

 

Библиогр.: 7 назв. Рис. 5.

Рецензенты: доктор техн. наук, профессор Е. И. Сковородников;

канд. физ.-мат. наук, доцент Г. А. Вершинин.

 

_______________________

© Омский гос. университет

путей сообщения, 2007

 

ОГЛАВЛЕНИЕ

 

Введение……………………………………………………………………………...5

1. Основы молекулярно-кинетической теории. Кинетическая энергия

хаотического движения молекул...……………………….….…..……..………..6

2. Уравнение состояния идеального газа.………………………....…….……......10

3. Теплоемкость идеального газа………………………………………………….14

4. Первое начало термодинамики. Процессы в газах…………………………….17

5. Энтропия………………………………………………………………………….21

6. Цикл Карно. Тепловые машины……………….………………………………..26

Библиографический список…………………..………………………………...….30

 

 

ВВЕДЕНИЕ

 

Решению задачи обязательно должна предшествовать проработка теоретического материала темы, на которую составлена задача. Для этого необходимо выбрать из библиографического списка какую-нибудь одну книгу и пользоваться все время ею, так как обозначения одних и тех же величин в разных книгах могут различаться. Если после тщательного изучения темы по одному учебнику материал не понят, целесообразно проработать теоретические вопросы на ту же тему в другом учебнике.

В данных методических указаниях даются ссылки на литературный источник с указанием его порядкового номера в библиографическом списке. Пособие [1] имеет преимущество в том, что в нем уделяется большое внимание качественной стороне физических явлений, чем, например, в работе [4]. Пособие [5] следует использовать лишь для углубленного изучения теоретического материала и при решении задач повышенной трудности. Примеры решения задач, а также основные формулы можно найти в сборнике [6]. Как известно, любая наука – это в первую очередь язык, система понятий. Для выяснения смысла любого физического термина неоценимую помощь окажет энциклопедический словарь [7].

Решение задачи начинайте не с поиска подходящей формулы, а попытайтесь понять, о каком физическом явлении идет речь в задаче. Рекомендуется переписать условие задачи в чистую тетрадь полностью, без сокращений. Дело в том, что иногда одно слово является ключевым, и если оно потеряно, то задача меняет смысл. Затем целесообразно сделать рисунок по условию задачи, если это возможно. Не исключено, что к одной задаче придется нарисовать несколько рисунков для более глубокого понимания ее условия.

Выполняя рисунок, вводите буквенные обозначения для физических величин. Успешное решение задачи в значительной степени зависит от того, насколько удачно эти обозначения сделаны. Обозначив физическую величину какой-нибудь буквой, строго придерживайтесь этого обозначения при решении задачи. Одна из типичных ошибок студентов состоит в том, что две физические величины они могут обозначать одной и той же буквой (например, – сопротивление проводника и универсальная газовая постоянная).

Чаще всего задачу целесообразно решать в общем виде. Получив расчетную формулу, проверьте размерности величин в правой и левой ее частях. Если размерности одинаковые, то это еще не гарантирует правильности решения, а если размерности разные, то задача точно решена неверно.

Обдумывая задачу, попытайтесь спрогнозировать ответ, хотя бы порядок его значения. Это поможет избежать ошибок при расчетах на микрокалькуляторах. Часто вычисления можно выполнить в уме и получить правильный результат с двумя значащими цифрами. В этом случае используйте следующие приближенные формулы, которые справедливы при : ; ; ; ; .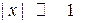

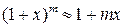Все задачи, приведенные в данных методических указаниях, разделены по уровням сложности (уровень сложности указан в скобках после номера задачи): самые простые имеют первый уровень, наиболее трудным задачам присвоен четвертый.

 

1. ОСНОВЫ Молекулярно-кинетической теории.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ХАОТИЧЕСКОГО ДВИЖЕНИЯ МОЛЕКУЛ

 

Статистический метод исследования систем, состоящих из многих частиц, базируется на трех положениях, которые называют основными положениями молекулярно-кинетической теории (МКТ) строения вещества. О значении основных положений МКТ кратко и выразительно сказал выдающийся американский физик Ричард Фейнман (1918 – 1988): «Если бы в результате какой-либо мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Мы считаем, что это атомная гипотеза (можете называть ее не гипотезой, а фактом, но это ничего не меняет): все тела состоят из атомов – маленьких телец, которые находятся в беспрерывном движении, притягиваются на небольшом расстоянии, но отталкиваются, если одно из них прижать к другому».

Итак, можно выделить три основные положения МКТ.

Первое положение: все тела состоят из частиц. Это могут быть атомы, молекулы, другие частицы. Например, вода состоит из молекул Н₂О, графит – из атомов углерода, кристалл золота – из однозарядных положительных ионов золота и свободных электронов проводимости.

Второе положение: частицы, из которых состоят все тела, находятся в непрерывном хаотическом движении. Количественной мерой этого движения является температура. В физике пользуются абсолютной температурой , которая связана с температурой по шкале Цельсия следующим соотношением:

 

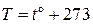, (1.1)

 

однако формула (1.1) не определяет абсолютную температуру. Удобнее всего определить абсолютную температуру с помощью выражения для средней кинетической энергии хаотического поступательного движения одной частицы:

 

, (1.2)

 

где = 1,38·10^–23 Дж/К – постоянная Больцмана.

Формулу (1.2) необходимо хорошо знать и уметь применять. Рассмотрим пример решения типичной задачи.

Задача 1. По современным представлениям температура в центре Солнца составляет 10⁷ К. Оцените среднеквадратичную скорость теплового движения протонов в центре Солнца.

Среднеквадратичная скорость , , где – масса протона. Комбинируя эти формулы с выражением (1.2), получаем:

 

, (1.3)

 

отсюда среднеквадратичная скорость

 

. (1.4)

 

При вычислении получаем: = 5·10⁵ м/с.

Третье положение: все частицы, из которых состоят тела, взаимодействуют, притягиваясь друг к другу на больших расстояниях и отталкиваясь на маленьких. Это хорошо видно на примере любого твердого вещества: необходимо приложить весьма значительное усилие, чтобы растянуть гвоздь (частицы, притягиваясь, препятствуют этому), а также большое усилие, чтобы сжать его (отталкивание частиц мешает этому).

В настоящее время установлено, что вещества состоят из молекул, а молекулы – из атомов. Есть вещества, молекулы которых содержат только один атом, такие вещества называются простыми (к ним принадлежат все инертные газы). Молекулы углекислого газа СО₂ или водяного пара Н₂О имеют сравнительно сложное строение. Иногда в состав одной молекулы входят тысячи атомов (молекулы полимеров или нуклеиновых кислот).

Размеры атомов и молекул чрезвычайно малы: типичный диаметр атома имеет порядок 1 ангстрем = 10^–10 м, однако в настоящее время с помощью современной техники (сканирующего туннельного электронного микроскопа) возможно «увидеть» отдельные атомы.

Обратите внимание на специфическую физическую величину, называемую количеством вещества, она измеряется в молях. По определению в одном моле вещества содержится 6,02·10²³ ( – число Авогадро) его структурных единиц (не обязательно молекул!). Введено количество вещества только для того, чтобы не писать каждый раз 10²³. Количество вещества связано с числом частиц , массой вещества и массой одной структурной единицы формулой:

. (1.5)

 

Одно и то же вещество может находиться в различных агрегатных состояниях (фазах). В земных условиях приходится иметь дело в основном с тремя агрегатными состояниями: твердым, жидким и газообразным. Четвертое состояние вещества – плазма – особенно распространено в космосе. Плазма – это вещество, значительная часть атомов и молекул которого ионизована. Заметная часть молекул воздуха ионизована в пламени, которое представляет собой низкотемпературную плазму. Чем выше температура пламени, тем выше степень ионизации. Вещество во внутренних слоях Солнца полностью ионизовано (высокотемпературная плазма).

Если в задаче не оговорено особо, то нужно считать, что вещество находится при нормальных условиях – давление равно 101 кПа, температура – 0^оС.

Важно помнить о том, что кинетическая энергия молекулы включает в себя не только энергию поступательного движения, но и энергию вращения, ко-

торая может быть разной в зависимости от числа степеней свободы и температуры. Атом не имеет вращательных степеней свободы. При комнатной температуре двухатомная молекула имеет две вращательные степени свободы, трехатомная и более сложные – три. Обычно азот, кислород, водород состоят из двухатомных молекул, а инертные газы – из одноатомных.

Подробно об основных положениях МКТ и кинетической энергии молекул описано в учебниках [1, с. 106 – 100, 126 – 132; 2, с. 82 – 90].

 

Задачи

1. (1) Аргон массой 40 мг находится в сферическом сосуде диаметром 80 мм под давлением 60 кПа. Найти внутреннюю энергию газа.

2. (1) Энергия хаотического движения 4 ∙10²⁷ молекул криптона составляет 20 МДж. Какова температура криптона в градусах Цельсия?

3. (1) Водород массой 300 г находится под давлением 80 кПа и имеет плотность 4,0 кг/м³. Найти энергию хаотического движения всех молекул газа при этих условиях.

4. (1) Найти энергию теплового движения молекул NH₃, находящихся в баллоне объемом 10 л при давлении 18,4 мм рт. ст. Какую часть энергии составляет энергия поступательного движения молекул?

5. (1) Баллон содержит азот массой 2000 мг при температуре 280 К. Определить суммарную кинетическую энергию поступательного движения всех молекул азота.

6. (1) Как и во сколько раз отличаются средние квадратичные скорости движения молекул азота и аргона в сухом атмосферном воздухе?

7. (1) Вычислить энергию двух молей фотонов с длиной волны 500 нм.

8. (2) В баллоне емкостью 50 л находится 0,12 кмоля газа при давлении 6,0 МПа. Определить среднюю кинетическую энергию поступательного движения одной молекулы газа.

9. (2) Сухой атмосферный воздух вблизи поверхности Земли состоит из азота (78,1 %), кислорода (21,0 %) и аргона (0,9 %). В тропическом воздухе содержится до 3 % водяных паров. Определить кинетическую энергию хаотического движения всех молекул аргона, находящихся в 15 м³ сухого атмосферного воздуха при нормальных условиях.

10. (2) Кинетическая энергия поступательного движения молекул азота, находящегося в баллоне объемом 20 л, равна 5000 Дж, а средняя квадратичная скорость его молекул – 2000 м/с. Какова концентрация молекул в сосуде?

 

2. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

 

Идеальный газ (ИГ) – это модель, позволяющая понять свойства очень многих природных систем и закономерности значительной части природных явлений. Модель ИГ – это система частиц, взаимодействующих друг с другом и со стенками сосуда только в кратковременных соударениях. Эта модель хорошо описывает свойства реальных газов и их смесей, например воздуха, причем не только при атмосферном давлении, но и при значениях давления гораздо выше и ниже атмосферного. Уравнение состояния ИГ можно записать в нескольких формах, представим некоторые из них:

 

; (2.1)

; (2.2)

. (2.3)

 

Чтобы пользоваться уравнениями (2.1) – (2.3), необходимо хорошо знать названия величин, входящих в них, и их размерность:

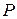– давление газ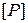а, = Па;

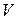– объем газа, 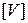= м³;

– масса газа, = кг;

– молярная масса газа, = кг · моль^–1;

– универсальная газовая постоянная, = 8,31 Дж·К^–1 · моль^–1;

– абсолютная температура газа, = К;

– плотность газа, = кг · м^–3;

– концентрация газа, = м^–3;

– постоянная Больцмана, = 1,38 · 10^–23 Дж · К^–1.

Рассмотрим пример решения несложной задачи на уравнение состояния ИГ.

Задача 2. Какова плотность аммиака при давлении 1200 торр и температуре 10^оС?

Дано: Газ – NH3 M = 17 г · моль–1 Р = 1200 торр Т = 10 + 273 К

Решение. Плотность газа входит в формулу (2.2), воспользуемся этой формой уравнения состояния ИГ. Молярную массу определим по таблице Менделеева. Для расчетов молярную массу необходимо выразить в килограммах-молях в минус первой степени (кг ·моль–1), давление – в паскалях (Па). Известно, что нормальное атмосферное давление 760 торр = 101 кПа, отсюда 1 торр = = 133 Па. Температуру следует выразить в кельвинах (К) (это уже сделано в краткой записи условия).

–?

Итак, получаем:

 

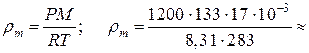1,15 кг · м^–3.

 

Если ИГ состоит из частиц нескольких сортов, то давление ИГ равно сумме значений давлений, которое оказывали бы частицы каждого сорта, если бы всех остальных не было (парциальные давления). Это очевидное утверждение называется законом Дальтона.

Каковы границы применимости модели ИГ? Чем пренебрегают, используя уравнение состояния ИГ (УСИГ)? Какой эффект можно ожидать, если выйти за рамки модели ИГ? Какие системы помимо реальных газов можно исследовать с помощью УСИГ? Эти вопросы, возникают у того, кто выходит за первый уровень знакомства с УСИГ. Попытаемся ответить на часть из них.

Итак, ИГ – это система частиц, которые взаимодействуют друг с другом и со стенками сосуда только при столкновениях. Однако согласно основным положениям МКТ все частицы, из которых состоят тела, все время хаотически движутся и взаимодействуют друг с другом. Значит, в модели ИГ пренебрегаем потенциальной энергией взаимодействия всех частиц между собой по сравнению с кинетической энергией их хаотического движения. Это, в свою очередь, означает, что внутренняя энергия ИГ состоит только из суммы кинетических энергий его частиц:

,(2.4)

где индекс «х» напоминает о том, что речь идет о хаотическом движении, «к» – о том, что это кинетическая энергия; величина – средняя кинетическая энергия хаотического движения одной частицы, она пропорциональна температуре, и если в роли частиц выступают атомы, то

 

. (2.5)

 

Как выглядит хаотическое движение частиц ИГ? Рассмотрим рис. 1, на котором видны следующие особенности движение частицы ИГ. Во-первых, от соударения до соударения частица движется прямолинейно (влиянием силы тяжести обычно можно пренебречь). Во-вторых, от соударения до соударения частица проходит разные пути, их количественной мерой является средняя длина

Рис. 1. Схематичная траектория одной частицы ИГ

свободного пробега частицы . В-третьих, скорость частицы после соударения непредсказуема: она может иметь любой модуль и любое направление. Это потому, что скорос-ти частиц, с которыми сталкивается выделенная частица, неизвестны. В-четвертых, намного больше размера частицы идеального газа .

В этом утверждении под частицей по-

нимается уже не материальная точка, а реальный структурный элемент той системы, для изучения которой используется модель ИГ.

До какой степени четвертое утверждение справедливо? Для выяснения этого необходимо иметь хотя бы приближенную формулу для оценки . Понятно, что должна быть обратно пропорционально концентрации и площади поперечного сечения частицы. Чтобы понять последнее утверждение, вообразите себе, что человек бежит через разреженную толпу. Ясно, что он будет чаще налетать на «препятствия», если они большого размера. Теперь составим структуру искомой формулы, ее точный вид таков:

. (2.6)

 

Итак, из формулы (2.6) следует, что . Для маленьких частиц 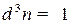, а с увеличением концентрации частиц модель ИГ практически не будет работать.

Модель ИГ применима не только для газов в обычном смысле этого слова, ее можно использовать и для электронов проводимости в металле, для электронов проводимости и дырок в полупроводниках, для нейтронов в слабо поглощающих средах, для фотонов и фононов. Правда, во всех этих случаях необходимо разобраться, с чем сталкиваются частицы и как вычислять длину их свободного пробега и скорость хаотического движения.

Подробнее о закономерностях поведения газов написано в книгах [1, с. 110 – 113, 136 – 140; 2, с. 86 – 88, 119 – 121].

 

Задачи

 

11. (1) Плотность газа при давлении 720 мм рт. ст. и температуре –20^оС равна 1,35 г/л. Найти массу киломоля газа.

12. (1) Найти количество вещества, содержащееся в 999 мм³ углекислого газа при температуре 4^оС и нормальном давлении.

13. (1) Сосуд емкостью 20 л содержит азот массой 8,2 г и водород массой 1,8 г при температуре 280 К. Определить давление смеси газов.

14. (2) Два баллона соединены трубкой с краном. В первом баллоне находится неон под давлением 100 кПа при температуре 40^оС, а во втором – углекислый газ под давлением 60 кПа при такой же температуре. Емкость первого баллона равна 1000 мл, второго – 3000. Какое давление установится в баллонах, если открыть кран? Температура при перемешивании газов не изменяется. Объемом трубки можно пренебречь.

15. (2) Баллон емкостью 40 л заполнен азотом при температуре 300 К. Когда часть азота израсходовали, давление в баллоне понизилось на 400 кПа, а температура не изменилась. Определить массу израсходованного азота.

16. (2) Воздушный шар имеет радиус 5,5 м. Воздух в нем нагрет до 30^оС. Температура окружающего воздуха равна –10^оС. Какова максимальная масса груза, который этот шар сможет поднять?

17. (2) В баллоне находился аргон при давлении 400 кПа и температуре 300 К. Затем 3/5 содержащегося в баллоне газа выпустили, а температура оставшегося газа понизилась до 240 К. Под каким давлением находится оставшийся в баллоне аргон?

18. (3) Баллон емкостью 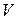, наполненный газом при давлении 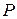и температуре , взвешивается, его масса равна . Из баллона откачивают газ, пока его давление не упадет до при той же температуре . Масса баллона с газом в этом случае составляет . Определить плотность газа при нормальных условиях – давлении и температуре .

19. (3) Три баллона емкостью 3000 мл, 7000 см³ и 5,0 л наполнены соответственно кислородом (2,0 атм), азотом (3,0 атм) и углекислым газом (0,60 атм) при одной и той же температуре. Баллоны соединяются между собой, причем образуется смесь той же температуры. Каково давление смеси?

20. (4) В сосуде находится смесь гелия и кислорода. При температуре –2,01^оC и давлении 90 кПа плотность этой смеси равна 440 мг/л. Каким станет давление смеси газов в сосуде, если из него удалить половину молекул кислорода?

 

3. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА

 

Теплоемкость тела определяется по формуле, Дж/К:

 

. (3.1)

 

Из формулы (3,1) понятно, что теплоемкость зависит от того, каким образом нагревать тело. Например, можно сообщать телу некоторое количество теплоты так, чтобы его температура не изменялась (изотермический процесс). Тогда , и теплоемкость формально оказывается бесконечной. Во всех задачах на теплоемкость газов имеются в виду теплоемкости при постоянном давлении и при постоянном объеме 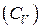, если не оговорено особо. Теплоемкость при постоянном давлении всегда больше, чем теплоемкость при постоянном объеме, так как количество теплоты расходуется не только на нагревание (т. е. увеличение внутренней энергии), но и на совершение работы.

Понятно, что теплоемкость тела пропорциональна его массе (объему), поэтому чаще пользуются удельной или молярной теплоемкостью. Удельная теплоемкость однородного вещества определяется по формуле, Дж/(кг∙К):

 

. (3.2)

 

Молярная теплоемкость однородного вещества рассчитывается по уравнению, Дж/(моль∙К):

 

. (3.3)

 

Наряду с определениями полезно знать выражение теплоемкости через число степеней свободы. При любых значениях температуры каждая молекула имеет три степени свободы, которые соответствуют поступательному движению абсолютно твердого тела вдоль трех декартовых осей. Двухатомная молекула при комнатной температуре (кроме упомянутых трех) имеет еще две степени свободы, которые соответствуют вращательному движению вокруг двух осей, перпендикулярных линии, соединяющей ядра атомов этой молекулы. Молекулы с числом атомов больше двух при комнатной температуре могут вращаться вокруг трех взаимно перпендикулярных осей. При высоких значениях температуры в многоатомных молекулах возбуждаются внутренние (колебательные) степени свободы, которые в данной работе не рассматриваются.

Таким образом, стандартный подход к решению задач на теплоемкость состоит в том, что одноатомная молекула имеет три степени свободы, двухатомная – пять, а молекула с числом атомов больше двух – шесть степеней свободы.

Внутренняя энергия идеального газа частиц связана со средней кинетической энергией одной частицы простой формулой:

. (3.4)

 

Обозначая число степеней свободы через , для классического идеального газа получаем:

. (3.5)

 

Из формулы (3.5) УСИГ, а также из первого начала термодинамики получаются следующие формулы для вычисления молярных теплоемкостей газов:

 

; (3.6а)

 

. (3.6б)

 

Отношение называется показателем адиабаты и входит в уравнение адиабатического процесса .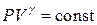

 

Задачи

 

21. (1) Найти разность между удельной теплоемкостью при постоянном давлении и удельной теплоемкостью при постоянном объеме для азота.

22. (2) Криптон находится в сосуде объемом 15 л при температуре –30^оС и давлении 1,5 атм. Какое количество теплоты нужно сообщить этому газу, чтобы нагреть его до 20^оС?

23. (2) Определить массу киломоля газа, удельная теплоемкость которого равна 285 Дж/(кг ∙ К) и 479 Дж/(кг ∙ К).

24. (3) Некоторый газ находится при температуре 350 К в баллоне емкостью 100 л под давлением 200 кПа. Теплоемкость этого газа при постоянном объеме равна 140 Дж/К. Определить отношение теплоемкостей газа.

25. (2). Некоторый газ при давлении 1000 кПа и температуре 400 К имеет удельный объем 0,104 м³/кг. Определить отношение его удельных теплоемкостей, если наибольшая из них равна 910 Дж/(кг ∙ К).

26. (2) Теплоемкость диэлектрических кристаллов, которые состоят из атомов одного сорта, при комнатной температуре ведет себя приблизительно так же, как и теплоемкость идеального газа, имеющего шесть степеней свободы. Определить теплоемкость кремниевой микросхемы, имеющей форму цилиндра высотой 3,5 мм и радиусом 5,3 мм. Плотность кремния – 2300 кг/м³.

27. (3) Некоторый газ при нормальных условиях имеет плотность 89 г/м³. Определить удельные теплоемкости этого газа.

28. (3) Смесь аргона и водорода имеет отношение удельных теплоемкостей 1,55. Сколько молекул аргона приходится на одну молекулу водорода в этой смеси?

29. (3) Смесь двух газов состоит из 20 г гелия и 350 г аммиака. Найти отношение молярных теплоемкостей этой смеси.

30. (3) Теплоемкость металлов при очень низких значениях температуры определяется в основном теплоемкостью идеального газа электронов проводимости, которая линейно зависит от температуры. Какое количество теплоты необходимо сообщить серебряной пылинке радиусом 2,5 мкм, чтобы нагреть ее от 5 до 10 К? Молярная теплоемкость серебра при температуре 5 К равна 7,07 мДж/(моль ∙ К), а при абсолютном нуле она обращается в нуль. Плотность серебра – 10,5 г/см³, его молярная масса – 107,9 г/моль.

 

4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ПРОЦЕССЫ В ГАЗАХ

 

Первый закон термодинамики, который есть не что иное, как закон сохранения энергии для тепловых процессов, можно выразить двумя формулами:

 

;(4.1а)

 

, (4.1б)

 

которые означают следующее. Рассмотрим состояние некоторого тела, например гвоздя (индекс «т»). Состояние тела характеризуется его внутренней энергией (ВЭ) 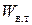, которая обычно пропорциональна температуре. Вся остальная вселенная (окружающая среда, индекс – «с») теперь интересует лишь постольку, поскольку она взаимодействует с телом (гвоздем). Внутреннюю энергию тела обычно можно изменить двумя способами.

Первый состоит в том, что среда сообщает (передает) телу некоторое количество теплоты 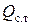. Если оно положительно, то приращение ВЭ тела положительно, т. е. ВЭ тела возрастает. Этого можно добиться, если положить гвоздь в горячую воду или нагреть его на пламени газовой плиты.

Можно увеличить ВЭ тела, не передавая ему тепло, а совершая над ним работу . Например, если ударить раз десять молотком по гвоздю, лежащему на рельсе, то все три тела (гвоздь, рельс и молоток) нагреются. Приращение ВЭ гвоздя в этом случае будет равно работе, которую над ним совершила среда (молоток и рельс). В соответствии с третьим законом Ньютона работа , которую среда совершила над телом, равна по модулю и противоположна по знаку работе , которую тело совершило над средой.

Если твердое тело или жидкость нагревают при комнатной температуре, то количество теплоты, переданное телу, можно вычислить по формуле:

 

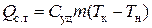, (4.2)

 

однако в некоторых случаях температура тела не изменяется, хотя телу передают тепло. Так происходит, например, при плавлении твердого тела или испарении жидкости. В этом случае количество теплоты вычисляется по формуле:

. (4.3)

В зависимости от того, для описания какого процесса используется формула (4.3), 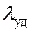в ней означает либо удельную теплоту плавления, либо удельную теплоту испарения. Между плавлением и испарением есть одно важное различие: плавление происходит при строго определенной температуре, а испарение – при любой.

Соотношения (4.2) и (4.3) справедливы лишь для простых случаев. Например, в формуле (4.2) предполагается, что теплоемкость не зависит от температуры и вещество однородное. Теплоемкость большинства веществ действительно слабо зависит от температуры при комнатной температуре. Однако с понижением температуры эта зависимость становится все более значимой. В связи с этим формулу (4.2) следует применять лишь для малого приращения температуры , в пределах которого теплоемкость можно считать постоянной с приемлемой для конкретной цели точностью. Формула (4.2) тогда приобретает вид:

(4.4)

и имеет гораздо более широкую область применимости.

Для решения многих задач удобно использовать первый закон термодинамики не в интегральном виде (4.1), а в следующей дифференциальной форме:

. (4.5)

Элементарная работа в общем случае выражается соотношением:

. (4.6)

Если тело уменьшает свой объем, т. е. , то работа внешних сил над телом положительна, а работа самого тела над окружающими его телами внешней среды в такой ситуации отрицательна.

Одним из основных понятий термодинамики является понятие равновесного состояния. Равновесным называется состояние замкнутой системы, которое не изменяется с течением времени. В таком состоянии во всех точках системы температура имеет одно и то же значение (чего не скажешь, например, о давлении и плотности).

Переход замкнутой системы из неравновесного состояния в равновесное называется релаксацией. Все релаксационные процессы необратимы. Хотя замкнутых систем в природе очень мало, иметь понятие о замкнутой системе очень важно, как о любой упрощенной модели.

Первый закон термодинамики, представленный в виде уравнения (4.5), справедлив для любых процессов, так как он является просто одной из форм закона сохранения энергии, однако применяют первый закон термодинамики обычно для квазистационарных (квазистатических) процессов.

При изучении природных процессов человек сталкивается почти всегда с открытыми системами, которые обмениваются с окружающей средой веществом и (или) энергией. Именно в открытых системах могут происходить квазистатические процессы: изотермический, изобарный и изохорный. Реальные природные процессы, в которых участвуют макроскопические тела, всегда необратимы.

Любой квазистатический процесс обратим: его можно осуществить в точности в обратном направлении так, что тело будет проходить через те же состояния, что и при прямом процессе. Чтобы эта абстракция соответствовала какому-нибудь реальному процессу, он должен происходить достаточно медленно. Обычно очень медленный процесс в земных условиях является изотермическим

(например, вытекание газа из баллона через узкую щель), а очень быстрый – адиабатическим (например, концентрация водяного пара при подъеме нагретых масс воздуха в верхние слои тропосферы). Примером изобарического процесса является процесс нагревания газа, находящегося под поршнем, если поршень может свободно перемещаться вверх-вниз.

Обратите внимание на особенности записи первого начала термодинамики (4.5). Значок «» указывает на то, что стоящая за ним величина не является функцией состояния, она – функция процесса. Иными словами, и не являются полными дифференциалами, т. е.

 

; (4.7а)

 

, (4.7б)

 

тогда

Поделиться:

Воспользуйтесь поиском по сайту: