 |
Решение с помощью программы Excel
|
|
|
|
1.2.1 Ввод исходных данных
Решим задачу, сформулированную в разделе 1.1. Для этого на рабочем листе введем ее числовые данные.
В первой строке таблицы находится заголовок, во второй - наименование переменных (продукции) (рис. 11).

Рис.11 - Экранная форма третьего задания
Третья строка отведена для оптимальных значений переменных, которые после решения появятся в ячейках ВЗ:ЕЗ (выделены цветом).
В четвертой строке в ячейках В4:Е4 заданы нижние граничные условия для переменных, а в ячейках В5:Е5 пятой строки – верхние граничные условия. Если в исходных данных нижняя граница какой-либо переменной не задана, то для экономических задач она принимается равной 0 (соответствующую ячейку можно не заполнять). В случае отсутствия заданной нижней границы некоторой переменной, берется произвольное число, значительно превышающее все другие значения верхней границы (в данном примере в ячейку С5 введено произвольное число 900).
В шестой строке заданы коэффициенты целевой функции, а ячейка F6, в рамке, зарезервирована для вычисления значения целевой функции и называется целевой ячейкой.
Строки с девятой по одиннадцатую содержат коэффициенты, знаки и правые части ограничений.
Предложенная форма таблицы удобна не только для выполнения расчетов, но и для документирования результатов моделирования, а также обмена идеями и улучшения взаимопонимания при работе «в команде» — группе лиц, ответственных за принятие решений.
Наглядность таблицы обеспечивается использованием заголовков, полужирного шрифта, подчеркивания текста и центрирования. Чтобы отобразить знак > или <, наберите знак > или < и затем подчеркните его.
1.2.2 Ввод формул
|
|
|
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно математической модели задачи 1.1, значение ЦФ определяется выражением

| (1.2) |
Используя обозначения соответствующих ячеек в Excel (см. рис.11), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
 . .
| (1.3) |
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter"
| =СУММПРОИЗВ(B$3:E$3;B6:E6), | (1.4) |
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение).
Существует другой способ задания функций в Excel с помощью режима "Вставить функции", который можно вызвать из меню "Формулы" или при нажатии кнопки "  "в строке формул. Так, например, формулу (1.4) можно задать следующим образом:
"в строке формул. Так, например, формулу (1.4) можно задать следующим образом:
· курсор установите в ячейку F6;
· нажав кнопку "  ",вызовите окно"Мастер функций – шаг 1 из 2";
",вызовите окно"Мастер функций – шаг 1 из 2";
· выберите в окне "Категория" категорию "Математические";
· в окне "Функция" выберите функцию СУММПРОИЗВ;
· в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.12);
· после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.12), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
|
|
|
Функций СУММПРОИЗВ позволяет вычислить сумму произведений двух массивов, первый из которых содержит значения переменных, а второй - коэффициенты целевой функции. Чтобы указать соответствующие диапазоны, можно воспользоваться кнопками свертывания, расположенными справа от полей ввода. Они позволяют временно убрать панель формул с экрана, чтобы удобнее было выделять диапазон на листе. Закончив выделение, щелкните кнопку снова для восстановления панели.
Ссылка на первый диапазон должна быть абсолютной, со знаками доллара перед каждой буквой и цифрой: $В$3:$Е$3 (чтобы изменить относительную ссылку на абсолютную, нажмите клавишу F4 непосредственно после ввода этой ссылки; если это не сделать сразу, то в дальнейшем ссылку сначала понадобится выделить и лишь затем нажать клавишу F4).
Ссылка на второй диапазон В4:Е4, напротив, должна быть относительной: что понадобится в дальнейшем при копировании формулы.

Рис.12 - Ввод формулы для расчета ЦФ в окно "Мастер функций"
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B9, C9, D9, E9 – 1-е ограничение; B10, C10, D10, E10 – 2-е ограничение и B11, C11, D11, E11 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.3.
Таблица 3
Формулы, описывающие ограничения модели (1.1)
| Левая часть ограничения | Формула Excel |
 или или

| =СУММПРОИЗВ(B$3:E$3;B9:E9) |
 или или

| =СУММПРОИЗВ(B$3:E$3;B10:E10) |
 или или
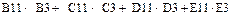
| =СУММПРОИЗВ(B$3:E$3;B11:E11) |
Как видно из табл.3, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого щелкните ячейку F4 правой кнопкой мыши и в контекстном меню выберите команду Копировать, затем выделите диапазон F8:F11, щелкните его правой кнопкой мыши и в контекстном меню выберите команду Специальная вставка. В группе Вставить открывшегося окна выберите параметр Формулы и щелкните кнопку ОК. Чтобы отменить движущуюся границу ячейки F4, нажмите клавишу Esc. Специальная вставка используется, чтобы копировалась только сама формула (без формата ячейки, к которому относятся, например, рамка).
|
|
|
При копировании относительная ссылка В4:Е4 будет меняться, указывая на массивы коэффициентов соответствующих ограничений, а абсолютная — $В$3:$Е$3 — останется неизменной.
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (после просмотра нажмите клавишу Esc) (рис.13).
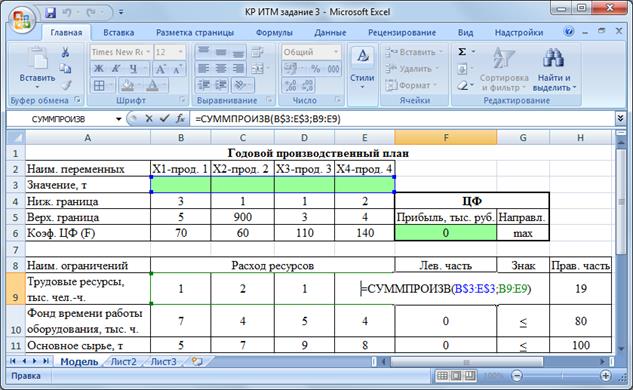
Рис.13 - Проверка правильности введения формулы в ячейку F9
для левой части ограничения по трудовым ресурсам
Если необходимо, чтобы отображались все введенные формулы, выберите вменю Формулы команду Показать формулы. Если таблицу с формулами необходимо напечатать, подберите ширину ее столбцов в соответствии с содержимым ячеек, как это было описано ранее.
После ввода формул вы можете подставлять в ячейки ВЗ:ЕЗ любые значения (количество выпускаемой продукции), получая соответствующую величину прибыли в ячейке F4 и объем израсходованных ресурсов в столбце Лев.часть.
1.2.3 Указание целевой функции и изменяемых ячеек
Теперь воспользуемся средством поиска решений.
Для этого в меню Данные в группе Анализ выберите команду Поиск решения, которая откроет одноименное окно.
Средство поиска решения является надстройкой (Надстройка. Вспомогательная программа, служащая для добавления в Microsoft Office специальных команд или возможностей.) Microsoft Office Excel, которая доступна при установке Microsoft Office или Microsoft Excel. Чтобы использовать эту надстройку в Excel, необходимо сначала загрузить ее следующим образом:
|
|
|
1. Нажмите кнопку Microsoft Office  , а затем щелкните Параметры Excel.
, а затем щелкните Параметры Excel.
2. Выберите команду Надстройки, а затем в окне Управление выберите пункт Надстройки Excel.
3. Нажмите кнопку Перейти.
4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК. Если Поиск решения отсутствует в списке поля Доступные надстройки, чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.
5. После загрузки надстройки для поиска решения в группе Анализ на вкладки Данные становится доступна команда Поиск решения.
При решении нашей задачи окно «Поиск решения» должно быть заполнено, как показано на рис. 14.

Рис. 14. Окно "Поиск решения" задачи (1.1)
В окне Поиск решения вы должны задать следующие параметры:
1) поставьте курсор в поле "Установить целевую ячейку" - для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу для вычисления целевой функции. Введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры. При вводе ссылок на ячейки удобно также пользоваться кнопками свертывания диалогового окна, расположенными справа от соответствующих полей;
2) введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению".
3) в поле "Изменяя ячейки" впишите адреса $B$3:$E$3. В нашем примере это ячейки, отведенные для значений переменных. Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
1.2.4 Добавление ограничений
Дня ввода ограничений следует нажать кнопку Добавить, открывающую окне два поля ввода (рис. 15):
Ссылка на ячейку — для указания ячейки или диапазона ячеек, на значения которых необходимо наложить ограничение («левая часть ограничения»).
Ограничение — для задания условия, накладывающегося на значения ячейки или диапазона, указанного в поле Ссылка на ячейку («правая часть ограничения»). В это поле можно ввести число, формулу, ссылку на ячейку или диапазон.
В раскрывающемся списке между этими полями можно выбрать необходимый знак (<=, =, >=), а также пункты цел (целое число) или двоич (двоичное число - 0 или 1), указывающие вид переменных при целочисленном решении.

Рис.15. Добавление ограничения по нижней границе переменных задачи
|
|
|
Для ввода ссылок на ячейки и диапазоны можно, как и раньше, воспользоваться кнопками свертывания диалогового окна, расположенными справа от полей ввода. Но поскольку окно Добавление ограничения и так достаточно невелико, удобнее просто перетащить его вниз экрана, поместив указатель мыши на заголовке. Затем следует щелкнуть в нужном поле этого окна и выделить на рабочем листе ячейку или диапазон, на который делается ссылка.
Каждое ограничение задачи можно вводить индивидуально. Однако когда знаки ограничений одинаковы, удобнее указывать их левые и правые части в виде диапазонов ячеек. После ввода каждого ограничения, кроме последнего, следует нажимать кнопку Добавить. При этом поля окна Добавление ограничения очищаются и можно вводить следующее ограничение. После ввода последнего из них, щелкните кнопку ОК, чтобы вернуться в окно Поиск решения, где вы увидите список всех введенных ограничений. При необходимости их изменения или удаления можно выделить любое из ограничений и нажать кнопку, соответственно, Изменить или Удалить.
1.2.5 Задание дополнительных параметров поиска решения
Для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис.16).

Рис.16. Параметры поиска решения, подходящие для большинства задач линейного программирования
Значения большинства параметров, установленные по умолчанию, подходят для решения большинства задач. Однако специально для решения задач линейного программирования следует установить два флажка:
Линейная модель — для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи и получения результатов после оптимизационного анализа;
Неотрицательные значения -чтобы переменные были неотрицательны.
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.
Флажок Показывать результаты итераций служит для приостановки поиска решения и просмотра результатов отдельных итераций.
Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, при максимизации прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Группа Оценки служит для выбора метода экстраполяции.
Группа Разности служит для выбора метода численного дифференцирования.
Группа Метод поиска служит для выбора алгоритма оптимизации.
Подтвердите установленные параметры нажатием кнопки "OK".
1.2.6 Нахождение решения
Вернувшись в окно Поиск решения, вы можете приступать к вычислениям. Для этого щелкните кнопку Выполнить. Результаты вычислений появятся на, рабочем листе, и одновременно откроется окно Результаты поиска с одним из сообщений, представленных на рис.17, 18 и 19.

Рис.17. Сообщение об успешном решении задачи

Рис.18. Сообщение при несовместной системе ограничений задачи
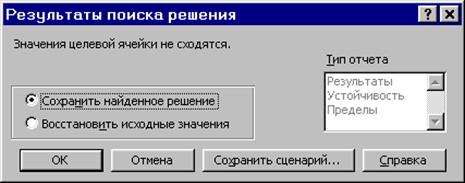
Рис.19. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда сообщения, представленные на рис. 17-19, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
В этом окне Результаты поиска решения" можно выбрать следующие параметры:
• Сохранить найденное решение — для сохранения найденного решения на рабочем листе.
• Восстановить исходные значения — для восстановления исходного вида рабочего листа.
• Тип отчета — для выдачи на отдельных рабочих листах отчетов, содержащих анализ полученных результатов. В списке можно выделить один или несколько типов отчета (в случае целочисленного решения доступен лишь один из них— Результаты). Отчет по результатам содержит ту же информацию, что и основной рабочий лист, отчет по пределам не представляет особой ценности, поэтому в дальнейшем подробно анализируется лишь наиболее интересный из отчетов — по устойчивости.
В нашей задаче выберите параметр Сохранить найденное решение,выделите в списке тип отчета — Результаты, Устойчивость и щелкните кнопку ОК. В рабочей книге появится новые листы с этими отчетами.
1.2.7 Анализ результатов
Результаты вычислений выглядят на рабочем листе, как показано на рис. 20.

Рис. 20. Результаты решения задачи линейного программирования
В ячейках ВЗ:ЕЗ выводится оптимальный производственный план, в ячейке F6 - максимальное значение прибыли.
В строках 9-11, содержащих ограничения на ресурсы, в столбце Лев.часть указаны объемы использованных ресурсов.
Отчет по результатам состоит из трех таблиц (рис.21):
1) таблица 1 содержит информацию о ЦФ;
2) таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
3) таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
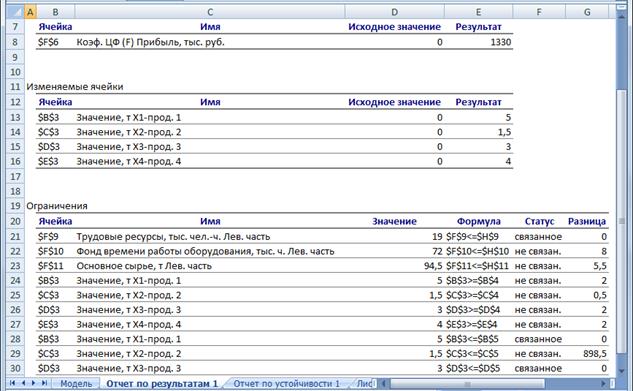
Рис. 21. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе "Статус" ("Состояние") соответствующее ограничение указывается как "связанное"; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается "не связан". В графе "Значение" приведены величины использованного ресурса.
Для граничных условий в графе "Разница" показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Так, если на ресурс наложено ограничение типа  , то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. Если на ресурс наложено ограничение типа
, то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. Если на ресурс наложено ограничение типа  , то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения
, то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения
Отчет поустойчивости состоит из двух таблиц (рис. 22).
Таблица 1 содержит информацию, относящуюся к переменным.
1. Результат решения задачи.
2. Нормированная стоимость, которая показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение.
Коэффициенты ЦФ.
4. Предельные значения приращения целевых коэффициентов, при которых сохраняется первоначальное оптимальное решение. При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).
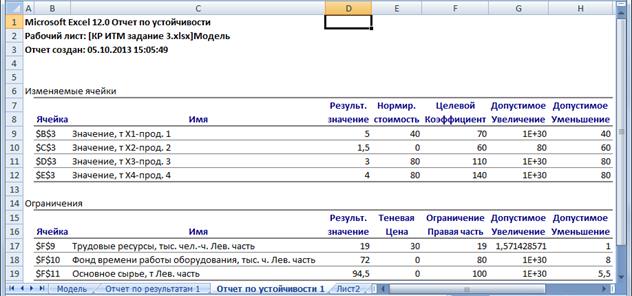
Рис. 22. Отчет по устойчивости решения задачи линейного
программирования
В первой из таблиц отчета выводится следующая информация:
В первых двух столбцах перечислены ячейки, в которых вычисляются значения переменных, и их имена.
В столбце Результ. Значение - найденное оптимальное решение (5;1,5; 3; 4).
В столбце Нормир. стоимость - двойственные оценки. Такая оценка может быть отлична от нуля только для нулевой переменной и показывает, на какую величину в целевой функции следует изменить коэффициент этой переменной, чтобы в оптимальном плане она приняла положительное значение (например, насколько увеличить цену изделия, чтобы его производить стало выгодно). Кроме того, эта оценка показывает, на какую величину ухудшится значение целевой функции, если уйти от оптимального плана, добавив в него единицу соответствующей продукции.
В столбце Целевой Коэффициент — коэффициенты целевой функции.
В последних двух столбцах — допустимые приращения коэффициентов целевой функции, при которых сохраняется прежнее оптимальное решение (при этом 1Е+30 означает 1030, то есть фактически +∞).
Во второй таблице выводится следующая информация:
В первых двух столбцах перечислены ячейки, в которых указаны левые части ограничений, и их имена.
В столбце Результ. Значение - значения левых частей ограничений (для ограничений на ресурсы — их использованное количество, для граничных условий — значение переменных в оптимальном плане).
В столбце Теневая Цена — теневые цены— двойственные оценки, показывающие, на какую величину изменится целевая функция при увеличении на единицу правой части ограничения или граничного условия, тогда как остальные данные неизменны (в частности при добавлении единицы соответствующего ресурса). Теневая цена — это максимальная цена, которую стоит платить за дополнительное количество дефицитного ресурса, чтобы его приобретение было выгодным.
В столбце Ограничение Правая часть — правые части ограничений (запасы ресурсов или граничные значения переменных).
В последних двух столбцах — допустимые приращения правых частей ограничений (запасов ресурсов или граничных значений переменных), при которых неизменны соответствующие теневые цены и в оптимальном решении сохраняется прежний набор ненулевых переменных (ассортимент продукции).
При добавлении допустимых приращений к правым частям ограничений получаются интервалы устойчивости.
После анализа результатов, можно изменить исходные данные на рабочем листе и повторить вычисления. При этом не понадобится повторно вводить ограничения или изменять параметры решения: достаточно лишь выбрать в меню Сервис команду Поиск решения и в открывшемся окне нажать кнопку Выполнить.
Вся информация, заданная в окне Поиск решения, постоянно хранится вмести с рабочим листом, к которому она относится. Не пропадет эта информация и при сохранении рабочей книги на диске.
|
|
|


