Задания 7. Механика. Установление соответствияЧасть 2

1. Груз изоб­ра­жен­но­го на ри­сун­ке пру­жин­но­го ма­ят­ни­ка может со­вер­шать гар­мо­ни­че­ские ко­ле­ба­ния между точ­ка­ми 1 и 3.

Пе­ри­од ко­ле­ба­ний груза Т. Гра­фи­ки А и Б пред­став­ля­ют из­ме­не­ния фи­зи­че­ских ве­ли­чин, ха­рак­те­ри­зу­ю­щих ко­ле­ба­ния груза после на­ча­ла ко­ле­ба­ний из по­ло­же­ния в точке 1.

 

ГРА­ФИ­КИ		ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ
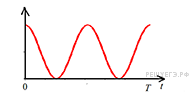
А) Б)		1) По­тен­ци­аль­ная энер­гия пру­жин­но­го ма­ят­ни­ка; 2) Ки­не­ти­че­ская энер­гия груза на пру­жи­не; 3) Про­ек­ция ско­ро­сти груза на ось Ох; 4) Про­ек­ция уско­ре­ния груза на ось

 

Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и фи­зи­че­ски­ми ве­ли­чи­на­ми, за­ви­си­мо­сти ко­то­рых от вре­ме­ни эти гра­фи­ки могут пред­став­лять.

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

A	Б

За­да­ние 7 № 2901

Ре­ше­ние.

С учё­том того, что ма­ят­ник на­чи­на­ет ко­ле­ба­ния из по­ло­же­ния в точке 1, для за­ви­си­мо­сти ко­ор­ди­на­ты груза от вре­ме­ни имеем Сле­до­ва­тель­но, для про­ек­ции ско­ро­сти по­лу­ча­ем:

 

 

Гра­фик А отоб­ра­жа­ет имен­но такую за­ви­си­мость от вре­ме­ни. Таким об­ра­зом, гра­фик А со­от­вет­ству­ет про­ек­ции ско­ро­сти груза на ось Ox (А — 3). Нули гра­фи­ка со­от­вет­ству­ют по­ло­же­ни­ям ма­ят­ни­ка в точка 1 и 3, а мак­си­му­мы и ми­ни­му­мы — по­ло­же­нию устой­чи­во­го рав­но­ве­сия. Легко ви­деть, что гра­фик Б пред­став­ля­ет по­тен­ци­аль­ную энер­гию пру­жин­но­го ма­ят­ни­ка (Б — 1). Дей­стви­тель­но,

 

 

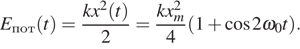
Мак­си­му­мы по­тен­ци­аль­ной энер­гии со­от­вет­ству­ют по­ло­же­ни­ям груза в точ­ках 1 и 3, а ми­ни­му­мы — точке 2.

Ответ: 31

2. Груз изоб­ра­жен­но­го на ри­сун­ке пру­жин­но­го ма­ят­ни­ка может со­вер­шать гар­мо­ни­че­ские ко­ле­ба­ния между точ­ка­ми 1 и 3. Пе­ри­од ко­ле­ба­ний груза Т.

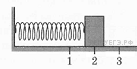
Гра­фи­ки А и Б пред­став­ля­ют из­ме­не­ния фи­зи­че­ских ве­ли­чин, ха­рак­те­ри­зу­ю­щих ко­ле­ба­ния груза после на­ча­ла ко­ле­ба­ний из по­ло­же­ния в точке 1.

 

ГРА­ФИ­КИ		ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ
А) Б)		1) По­тен­ци­аль­ная энер­гия пру­жин­но­го ма­ят­ни­ка; 2) Ки­не­ти­че­ская энер­гия груза на пру­жи­не; 3) Про­ек­ция ско­ро­сти груза на ось Ох; 4) Про­ек­ция уско­ре­ния груза на ось Ох.

 

Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и фи­зи­че­ски­ми ве­ли­чи­на­ми, за­ви­си­мо­сти ко­то­рых от вре­ме­ни эти гра­фи­ки могут пред­став­лять.

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

A	Б

За­да­ние 7 № 2902

Ре­ше­ние.

С уче­том того, что ма­ят­ник на­чи­на­ет ко­ле­ба­ния из по­ло­же­ния в точке 1, для за­ви­си­мо­сти ко­ор­ди­на­ты груза от вре­ме­ни имеем Сле­до­ва­тель­но, для про­ек­ции ско­ро­сти по­лу­ча­ем:

 

 

Легко ви­деть, что гра­фик А пред­став­ля­ет ки­не­ти­че­скую энер­гию груза на пру­жи­не (А — 2). Дей­стви­тель­но,

 

 

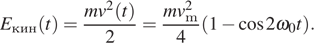
Ми­ни­мум ки­не­ти­че­ской энер­гии со­от­вет­ству­ют по­ло­же­ни­ям груза в точ­ках 1 и 3, а мак­си­му­мы — точке 2. В свою оче­редь для про­ек­ции уско­ре­ния по­лу­ча­ем:

 

 

Гра­фик Б отоб­ра­жа­ет имен­но такую за­ви­си­мость от вре­ме­ни. Таким об­ра­зом, гра­фик Б со­от­вет­ству­ет про­ек­ции уско­ре­ния груза на ось Ox (Б — 4).

Ответ: 24

3. Ма­те­ма­ти­че­ский ма­ят­ник со­вер­ша­ет гар­мо­ни­че­ские ко­ле­ба­ния между точ­ка­ми 1 и 2.

 

 

Гра­фи­ки А и Б пред­став­ля­ют за­ви­си­мость от вре­ме­ни t фи­зи­че­ских ве­ли­чин, ха­рак­те­ри­зу­ю­щих ко­ле­ба­ния. В на­чаль­ный мо­мент вре­ме­ни ма­ят­ник на­хо­дил­ся в по­ло­же­нии 1.

 

ГРА­ФИ­КИ		ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ
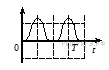
А) Б)		1) Про­ек­ция ско­ро­сти на ось Оy; 2) Про­ек­ция уско­ре­ния на ось Ох; 3) Ки­не­ти­че­ская энер­гия ма­ят­ни­ка; 4) По­тен­ци­аль­ная энер­гия ма­ят­ни­ка от­но­си­тель­но по­верх­но­сти земли.

 

Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и фи­зи­че­ски­ми ве­ли­чи­на­ми, за­ви­си­мо­сти ко­то­рых от вре­ме­ни эти гра­фи­ки могут пред­став­лять.

 

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

A	Б

За­да­ние 7 № 2907

Ре­ше­ние.

Счи­тая ко­ле­ба­ния ма­те­ма­ти­че­ско­го ма­ят­ни­ка ма­лы­ми, с учётом того, что они на­чи­на­ют­ся из по­ло­же­ния 1, для за­ви­си­мо­сти ко­ор­ди­на­ты ма­ят­ни­ка от вре­ме­ни имеем

 

 

Сле­до­ва­тель­но, для про­ек­ции уско­ре­ния по­лу­ча­ем:

 

 

Гра­фик А отоб­ра­жа­ет имен­но такую за­ви­си­мость от вре­ме­ни. Таким об­ра­зом, гра­фик А со­от­вет­ству­ет про­ек­ции уско­ре­ния на ось Ox (А — 2). Нули гра­фи­ка со­от­вет­ству­ют по­ло­же­нию рав­но­ве­сия, а мак­си­му­мы и ми­ни­му­мы — по­ло­же­ни­ям 1 и 2. Легко ви­деть, что гра­фик Б пред­став­ля­ет ки­не­ти­че­скую энер­гию ма­ят­ни­ка (Б — 3). Дей­стви­тель­но,

 

 

Мак­си­му­мы ки­не­ти­че­ской энер­гии со­от­вет­ству­ют по­ло­же­нию рав­но­ве­сия, в ко­то­ром ско­рость ма­ят­ни­ка мак­си­маль­на, а ми­ни­му­мы — край­ним по­ло­же­ни­ям 1 и 2, в ко­то­рых ско­рость об­ра­ща­ет­ся в ноль.

Ответ: 23

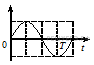
4. Ма­те­ма­ти­че­ский ма­ят­ник со­вер­ша­ет гар­мо­ни­че­ские ко­ле­ба­ния между точ­ка­ми 1 и 2.

 

 

Гра­фи­ки А и Б пред­став­ля­ют за­ви­си­мость от вре­ме­ни t фи­зи­че­ских ве­ли­чин, ха­рак­те­ри­зу­ю­щих ко­ле­ба­ния. В на­чаль­ный мо­мент вре­ме­ни t ма­ят­ник на­хо­дил­ся в по­ло­же­нии 1.

 

ГРА­ФИ­КИ		ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ
А) Б)		1) По­тен­ци­аль­ная энер­гия ма­ят­ни­ка от­но­си­тель­но по­верх­но­сти земли; 2) Ки­не­ти­че­ская энер­гия ма­ят­ни­ка; 3) Про­ек­ция уско­ре­ния на ось Ох. 4) Про­ек­ция ско­ро­сти на ось Ох.

 

Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и фи­зи­че­ски­ми ве­ли­чи­на­ми, за­ви­си­мо­сти ко­то­рых от вре­ме­ни эти гра­фи­ки могут пред­став­лять.

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

A	Б

За­да­ние 7 № 2908

Ре­ше­ние.

Счи­тая ко­ле­ба­ния ма­те­ма­ти­че­ско­го ма­ят­ни­ка ма­лы­ми, с уче­том того, что они на­чи­на­ют­ся из по­ло­же­ния 1, для за­ви­си­мо­сти ко­ор­ди­на­ты ма­ят­ни­ка от вре­ме­ни имеем

.

Сле­до­ва­тель­но, для про­ек­ции ско­ро­сти по­лу­ча­ем:

.

Гра­фик А отоб­ра­жа­ет имен­но такую за­ви­си­мость от вре­ме­ни. Таким об­ра­зом, гра­фик А со­от­вет­ству­ет про­ек­ции ско­ро­сти на ось (А — 4). Нули гра­фи­ка со­от­вет­ству­ют край­ним по­ло­же­ни­ям 1 и 2, а мак­си­му­мы и ми­ни­му­мы — по­ло­же­нию рав­но­ве­сия. Легко ви­деть, что гра­фик Б пред­став­ля­ет ки­не­ти­че­скую энер­гию ма­ят­ни­ка (Б — 2). Дей­стви­тель­но,

.

Мак­си­му­мы ки­не­ти­че­ской энер­гии со­от­вет­ству­ют по­ло­же­нию рав­но­ве­сия, в ко­то­ром ско­рость ма­ят­ни­ка мак­си­маль­на, а ми­ни­му­мы — край­ним по­ло­же­ни­ям 1 и 2, в ко­то­рых ско­рость об­ра­ща­ет­ся в ноль.

Ответ: 42

5. Ка­мень бро­си­ли вер­ти­каль­но вверх с по­верх­но­сти земли. Счи­тая со­про­тив­ле­ние воз­ду­ха малым, уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и фи­зи­че­ски­ми ве­ли­чи­на­ми, за­ви­си­мо­сти ко­то­рых от вре­ме­ни эти гра­фи­ки могут пред­став­лять.

 

ГРА­ФИ­КИ		ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ
		1) Про­ек­ция ско­ро­сти камня ; 2) Ки­не­ти­че­ская энер­гия камня; 3) Про­ек­ция уско­ре­ния камня ; 4) Энер­гия вза­и­мо­дей­ствия камня с Зем­лей.

 

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

A	Б

За­да­ние 7 № 2909

Ре­ше­ние.

Пре­не­бре­гая силой со­про­тив­ле­ния воз­ду­ха, за­клю­ча­ем, что на ка­мень дей­ству­ет толь­ко сила тя­же­сти, ко­то­рая со­об­ща­ет ему по­сто­ян­ное уско­ре­ние сво­бод­но­го па­де­ния, на­прав­лен­ное вниз. Тогда за­ви­си­мость про­ек­ции ско­ро­сти камня от вре­ме­ни при­об­ре­та­ет вид . Гра­фик Б отоб­ра­жа­ет имен­но такую за­ви­си­мость от вре­ме­ни. Таким об­ра­зом, гра­фик Б со­от­вет­ству­ет про­ек­ции ско­ро­сти камня (Б — 1). Легко ви­деть, что гра­фик А пред­став­ля­ет ки­не­ти­че­скую энер­гию камня (А — 2). Дей­стви­тель­но,

.

Ответ: 21

6. Уста­но­ви­те со­от­вет­ствие между по­ня­ти­я­ми и их опре­де­ле­ни­я­ми: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го и вне­си­те в стро­ку от­ве­тов вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ПО­НЯ­ТИЕ		ОПРЕ­ДЕ­ЛЕ­НИЕ
А) За­мкну­тая си­сте­ма Б) Им­пульс тела В) По­пе­реч­ная волна Г) Ки­не­ти­че­ская энер­гия		1) Волна, в ко­то­рой дви­же­ние ча­стиц среды про­ис­хо­дит в на­прав­ле­нии рас­про­стра­не­ния волны. 2) Си­сте­ма тел, вза­и­мо­дей­ству­ю­щих толь­ко между собой и не вза­и­мо­дей­ству­ю­щих с те­ла­ми, не вхо­дя­щи­ми в эту си­сте­му. 3) Ве­ли­чи­на, рав­ная про­из­ве­де­нию массы тела на его ско­рость. 4) Волна, в ко­то­рой ча­сти­цы среды пе­ре­ме­ща­ют­ся пер­пен­ди­ку­ляр­но на­прав­ле­нию рас­про­стра­не­ния волны. 5) Си­сте­мы от­сче­та, в ко­то­рых тело со­хра­ня­ет со­сто­я­ние покоя или рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния до тех пор, пока на него не по­дей­ству­ют дру­гие тела или дей­ствия дру­гих тел ком­пен­си­ру­ют­ся. 6) Ве­ли­чи­на, рав­ная по­ло­ви­не про­из­ве­де­ния массы тела на квад­рат его ско­ро­сти.

 

A	Б	В	Г

За­да­ние 7 № 3100

Ре­ше­ние.

За­мкну­той си­сте­мой на­зы­ва­ет­ся си­сте­ма тел, вза­и­мо­дей­ству­ю­щих толь­ко между собой и не вза­и­мо­дей­ству­ю­щих с те­ла­ми, не вхо­дя­щи­ми в эту си­сте­му (А — 2). Им­пульс тела пред­став­ля­ет собой ве­ли­чи­ну, рав­ную про­из­ве­де­нию массы тела на его ско­рость (Б — 3). По­пе­реч­ная волна — это волна, в ко­то­рой ча­сти­цы среды пе­ре­ме­ща­ют­ся пер­пен­ди­ку­ляр­но на­прав­ле­нию рас­про­стра­не­ния волны (В — 4). Ки­не­ти­че­ская энер­гия тела опре­де­ля­ет­ся как ве­ли­чи­на, рав­ная по­ло­ви­не про­из­ве­де­ния массы тела на квад­рат его ско­ро­сти (Г — 6).

Ответ: 2346

7. Груз мас­сой , под­ве­шен­ный к длин­ной не­рас­тя­жи­мой нити дли­ной , со­вер­ша­ет ко­ле­ба­ния с пе­ри­о­дом 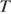. Угол мак­си­маль­но­го от­кло­не­ния равен . Что про­изой­дет с пе­ри­о­дом ко­ле­ба­ний, мак­си­маль­ной ки­не­ти­че­ской энер­ги­ей и ча­сто­той ко­ле­ба­ний ни­тя­но­го ма­ят­ни­ка, если при не­из­мен­ном мак­си­маль­ном угле от­кло­не­ния груза уве­ли­чить длину нити?

К каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го и вне­си­те в стро­ку от­ве­тов вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИЗ­МЕ­НЕ­НИЕ ВЕ­ЛИ­ЧИ­НЫ
А) Пе­ри­од ко­ле­ба­ний Б) Мак­си­маль­ная ки­не­ти­че­ская энер­гия В) Ча­сто­та ко­ле­ба­ний		1) Уве­ли­чи­ва­ет­ся 2) Умень­ша­ет­ся 3) Не из­ме­нит­ся

 

A	Б	В

За­да­ние 7 № 3103

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний свя­зан с дли­ной нити и ве­ли­чи­ной уско­ре­ния сво­бод­но­го па­де­ния со­от­но­ше­ни­ем . Сле­до­ва­тель­но, при уве­ли­че­нии длины нити пе­ри­од ко­ле­ба­ний уве­ли­чит­ся (А — 1). Ча­сто­та об­рат­но про­пор­ци­о­наль­на пе­ри­о­ду, зна­чит, ча­сто­та умень­шит­ся (В — 2). При ко­ле­ба­ни­ях ни­тя­но­го ма­ят­ни­ка вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии, по­сколь­ку на него не дей­ству­ет ни­ка­ких внеш­них сил, со­вер­ша­ю­щих ра­бо­ту. Будем от­счи­ты­вать по­тен­ци­аль­ную энер­гию ма­ят­ни­ка от по­ло­же­ния устой­чи­во­го рав­но­ве­сия. Тогда мак­си­маль­ная ки­не­ти­че­ская энер­гия груза будет равна его по­тен­ци­аль­ной энер­гии во время мак­си­маль­но­го от­кло­не­ния из по­ло­же­ния рав­но­ве­сия.

Из ри­сун­ка видно, что при уве­ли­че­нии длины нити и не­из­мен­ном угле мак­си­маль­но­го от­кло­не­ния, вы­со­та подъ­ема груза над по­ло­же­ни­ем рав­но­ве­сия уве­ли­чи­ва­ет­ся 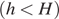, а зна­чит, уве­ли­чи­ва­ет­ся его по­тен­ци­аль­ная энер­гия в этом по­ло­же­нии. Таким об­ра­зом, при уве­ли­че­нии длины нити и не­из­мен­ном угле мак­си­маль­ная ки­не­ти­че­ская энер­гия груза уве­ли­чи­ва­ет­ся(Б — 1).

Ответ: 112

8. Груз, под­ве­шен­ный на пру­жи­не, со­вер­ша­ет вы­нуж­ден­ные гар­мо­ни­че­ские ко­ле­ба­ния под дей­стви­ем силы, ме­ня­ю­щей­ся с ча­сто­той . Уста­но­ви­те со­от­вет­ствие между фи­зи­че­ски­ми ве­ли­чи­на­ми и ча­сто­той их из­ме­не­ния в этом про­цес­се. К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те нуж­ную по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ЧА­СТО­ТА ИХ ИЗ­МЕ­НЕ­НИЯ
А) Ки­не­ти­че­ская энер­гия Б) Ско­рость		1) 2) 3) 4)

 

A	Б

За­да­ние 7 № 3131

Ре­ше­ние.

Под дей­стви­ем силы, ме­ня­ю­щей­ся с ча­сто­той , груз на пру­жи­не со­вер­ша­ет вы­нуж­ден­ные гар­мо­ни­че­ские ко­ле­ба­ния с такой же ча­сто­той. Сле­до­ва­тель­но, закон из­ме­не­ния ко­ор­ди­на­ты груза со вре­ме­нем имеет вид Таким об­ра­зом, закон из­ме­не­ния ско­ро­сти со вре­ме­нем: . От­сю­да по­лу­ча­ем, что ча­сто­та из­ме­не­ния ско­ро­сти груза также равна (Б — 2). Ки­не­ти­че­ская энер­гия груза из­ме­ня­ет­ся по за­ко­ну 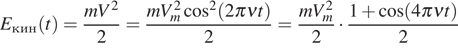. Сле­до­ва­тель­но, ча­сто­та из­ме­не­ния ки­не­ти­че­ской энер­гии равна (А — 3).

Ответ: 32

9. Шарик висит на нити. В нем за­стре­ва­ет пуля, ле­тя­щая го­ри­зон­таль­но, в ре­зуль­та­те чего нить от­кло­ня­ет­ся на не­ко­то­рый угол. Как из­ме­нят­ся при уве­ли­че­нии массы ша­ри­ка сле­ду­ю­щие три ве­ли­чи­ны: им­пульс, по­лу­чен­ный ша­ри­ком в ре­зуль­та­те по­па­да­ния в него пули; ско­рость, ко­то­рая будет у ша­ри­ка тот­час после удара; угол от­кло­не­ния нити? Пуля за­стре­ва­ет очень быст­ро. Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

1) уве­ли­чит­ся;

2) умень­шит­ся;

3) не из­ме­нит­ся.

 

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

 

Им­пульс, по­лу­чен­ный ша­ри­ком в ре­зуль­та­те по­па­да­ния в него пули	Ско­рость, ко­то­рая будет у ша­ри­ка тот­час после удара	Угол от­кло­не­ния нити

 

По­яс­не­ние. Для вы­пол­не­ния этого за­да­ния надо знать два за­ко­на со­хра­не­ния — им­пуль­са и ме­ха­ни­че­ской энер­гии. В про­цес­се за­стре­ва­ния си­сте­ма «шарик + пуля» яв­ля­ет­ся в го­ри­зон­таль­ном на­прав­ле­нии изо­ли­ро­ван­ной, а зна­чит, ее им­пульс со­хра­ня­ет­ся при этом не­из­мен­ным и рав­ным им­пуль­су ле­тя­щей пули. Это дает воз­мож­ность уста­но­вить, каким об­ра­зом вли­я­ет масса ша­ри­ка на им­пульс всей си­сте­мы тот­час после за­стре­ва­ния. Что же ка­са­ет­ся угла от­кло­не­ния нити, то он тем боль­ше, чем боль­ше ско­рость си­сте­мы — в со­от­вет­ствии с за­ко­ном со­хра­не­ния ме­ха­ни­че­ской энер­гии.

За­да­ние 7 № 3134

Ре­ше­ние.

Ско­рость ша­ри­ка с за­стряв­шей в нем пулей сразу после удара можно найти из за­ко­на со­хра­не­ния им­пуль­са, она равна: , где и — массы пули и ша­ри­ка со­от­вет­ствен­но, а 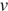— ско­рость пули до удара. От­сю­да видно, что при уве­ли­че­нии массы ша­ри­ка ско­рость, ко­то­рая у него будет сразу после удара, умень­ша­ет­ся.

Им­пульс, пе­ре­дан­ный ша­ри­ку равен Из вы­ра­же­ния для им­пуль­са ша­ри­ка видно, что с уве­ли­че­ни­ем массы ша­ри­ка им­пульс, пе­ре­дан­ный ему уве­ли­чи­ва­ет­ся.

При дви­же­нии вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии, по­сколь­ку на шарик не дей­ству­ет ни­ка­ких внеш­них сил, со­вер­ша­ю­щих ра­бо­ту. Угол от­кло­не­ния тем боль­ше, чем выше под­ни­мет­ся шарик, а вы­со­ту подъ­ема можно найти из за­ко­на со­хра­не­ния энер­гии:

.

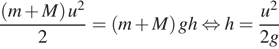Сле­до­ва­тель­но при уве­ли­че­нии массы ша­ри­ка угол от­кло­не­ния, как и ско­рость, умень­ша­ет­ся.

 

Ответ: 122.

Ответ: 122

10. Те­леж­ка с пес­ком стоит на рель­сах. В неё по­па­да­ет сна­ряд, ле­тя­щий го­ри­зон­таль­но вдоль рель­сов. Как из­ме­нят­ся при умень­ше­нии ско­ро­сти сна­ря­да сле­ду­ю­щие три ве­ли­чи­ны: ско­рость си­сте­мы «те­леж­ка + сна­ряд», им­пульс этой си­сте­мы, её ки­не­ти­че­ская энер­гия? Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

1)уве­ли­чит­ся;

2)умень­шит­ся;

3)не из­ме­нит­ся.

 

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

 

Ско­рость си­сте­мы	Им­пульс си­сте­мы	Ки­не­ти­че­ская энер­гия

За­да­ние 7 № 3136

Ре­ше­ние.

На си­сте­му «те­леж­ка + сна­ряд» в го­ри­зон­таль­ном на­прав­ле­нии не дей­ству­ет ни­ка­ких внеш­них сил, а зна­чит, в этом на­прав­ле­нии вы­пол­ня­ет­ся закон со­хра­не­ния им­пуль­са. Сле­до­ва­тель­но, им­пульс си­сте­мы равен им­пуль­су сна­ря­да до удара. Если умень­шить на­чаль­ную ско­рость сна­ря­да, то умень­ша­ет­ся им­пульс сна­ря­да, а зна­чит, и им­пульс си­сте­мы «те­леж­ка + сна­ряд» после удара. Раз умень­ша­ет­ся им­пульс си­сте­мы, умень­ша­ет­ся и ско­рость си­сте­мы. Ки­не­ти­че­ская энер­гия те­леж­ки с за­стряв­шим в ней сна­ря­дом про­пор­ци­о­наль­на квад­ра­ту ско­ро­сти си­сте­мы. Сле­до­ва­тель­но, ки­не­ти­че­ская энер­гия тоже умень­ша­ет­ся при умень­ше­нии ско­ро­сти сна­ря­да.

Ответ: 222

11. Мас­сив­ный шарик, под­ве­шен­ный к по­тол­ку на упру­гой пру­жи­не, со­вер­ша­ет вер­ти­каль­ные гар­мо­ни­че­ские ко­ле­ба­ния. Как ведут себя ско­рость и уско­ре­ние ша­ри­ка в мо­мент, когда шарик про­хо­дит по­ло­же­ние рав­но­ве­сия, дви­га­ясь вниз?

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ МО­ДУЛЬ И НА­ПРАВ­ЛЕ­НИЕ
А) Ско­рость ша­ри­ка Б) Уско­ре­ние ша­ри­ка		1) До­сти­га­ет мак­си­му­ма; на­прав­ле­ние вверх 2) До­сти­га­ет мак­си­му­ма; на­прав­ле­ние вниз 3) Мо­дуль равен нулю

 

A	Б

За­да­ние 7 № 3165

Ре­ше­ние.

При гар­мо­ни­че­ских ко­ле­ба­ни­ях за­ко­ны из­ме­не­ния со вре­ме­нем от­кло­не­ния ша­ри­ка из по­ло­же­ния рав­но­ве­сия и его ско­ро­сти имеют вид и со­от­вет­ствен­но. В по­ло­же­нии рав­но­ве­сия, когда ско­рость ша­ри­ка до­сти­га­ет сво­е­го мак­си­му­ма При дви­же­нии вниз ско­рость ша­ри­ка есте­ствен­но на­прав­ле­на вниз (А — 2). Уско­ре­ние ша­ри­ка в по­ло­же­нии рав­но­ве­сия, на­про­тив, равно нулю, по­сколь­ку рав­но­дей­ству­ю­щая всех сил, дей­ству­ю­щих на шарик, в этот мо­мент равна нулю (Б — 3).

Ответ: 23

12. Гиря мас­сой 2 кг под­ве­ше­на на длин­ном тон­ком шнуре. Если ее от­кло­нить от по­ло­же­ния рав­но­ве­сия на 10 см, а затем от­пу­стить, она со­вер­ша­ет сво­бод­ные ко­ле­ба­ния как ма­те­ма­ти­че­ский ма­ят­ник с пе­ри­о­дом 1 с. Что про­изой­дет с пе­ри­о­дом, мак­си­маль­ной по­тен­ци­аль­ной энер­ги­ей гири и ча­сто­той ее ко­ле­ба­ний, если на­чаль­ное от­кло­не­ние гири будет равно 20 см?

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ИЗ­МЕ­НЕ­НИЯ
А) Пе­ри­од Б) Ча­сто­та В) Мак­си­маль­ная по­тен­ци­аль­ная энер­гия гири		1) Уве­ли­чит­ся 2) Умень­шит­ся 3) Не из­ме­нит­ся

 

A	Б	В

За­да­ние 7 № 3167

Ре­ше­ние.

Пе­ри­од сво­бод­ных ко­ле­ба­ний ма­те­ма­ти­че­ско­го ма­ят­ни­ка за­ви­сит толь­ко от длины нити и ве­ли­чи­ны уско­ре­ния сво­бод­но­го па­де­ния: . Сле­до­ва­тель­но, при уве­ли­че­нии на­чаль­но­го от­кло­не­ния гири в два раза, пе­ри­од не из­ме­нит­ся (А — 3). Ча­сто­та об­рат­но про­пор­ци­о­наль­на пе­ри­о­ду, зна­чит, ча­сто­та также не из­ме­нит­ся (Б — 3). С дру­гой сто­ро­ны, чем боль­ше на­чаль­ное от­кло­не­ние гири, тем выше она на­хо­дит­ся над по­ло­же­ни­ем рав­но­ве­сия в мо­мен­ты мак­си­маль­но­го от­кло­не­ния. Таким об­ра­зом, при уве­ли­че­нии на­чаль­но­го от­кло­не­ния гири ее мак­си­маль­ная по­тен­ци­аль­ная энер­гия уве­ли­чит­ся (В — 1).

Ответ: 331

13. Ка­мень бро­шен вер­ти­каль­но вверх. Из­ме­ня­ют­ся ли пе­ре­чис­лен­ные в пер­вом столб­це фи­зи­че­ские ве­ли­чи­ны во время его дви­же­ния вверх и если из­ме­ня­ют­ся, то как? Уста­но­ви­те со­от­вет­ствие между фи­зи­че­ски­ми ве­ли­чи­на­ми, пе­ре­чис­лен­ны­ми в пер­вом столб­це, и воз­мож­ны­ми ви­да­ми их из­ме­не­ний, пе­ре­чис­лен­ны­ми во вто­ром столб­це. Вли­я­ни­ем со­про­тив­ле­ния воз­ду­ха пре­не­бречь.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ИЗ­МЕ­НЕ­НИЯ
А) Ско­рость Б) Уско­ре­ние В) Ки­не­ти­че­ская энер­гия Г) По­тен­ци­аль­ная энер­гия		1) Уве­ли­чит­ся 2) Умень­шит­ся 3) Не из­ме­нит­ся

 

A	Б	В	Г

За­да­ние 7 № 3168

Ре­ше­ние.

Пре­не­бре­гая силой со­про­тив­ле­ния воз­ду­ха, за­клю­ча­ем, что на ка­мень дей­ству­ет толь­ко сила тя­же­сти, ко­то­рая со­об­ща­ет ему по­сто­ян­ное уско­ре­ние сво­бод­но­го па­де­ния (Б — 3), на­прав­лен­ное вниз. По­сколь­ку при дви­же­нии камня вверх уско­ре­ние и ско­рость камня на­прав­ле­ны в раз­ные сто­ро­ны, ско­рость камня умень­ша­ет­ся (А — 2). Сле­до­ва­тель­но, ки­не­ти­че­ская энер­гия, про­пор­ци­о­наль­ная квад­ра­ту ско­ро­сти, также умень­ша­ет­ся (В — 2). При дви­же­нии камня вверх его вы­со­та над по­верх­но­стью земли уве­ли­чи­ва­ет­ся, от­сю­да за­клю­ча­ем, что по­тен­ци­аль­ная энер­гия камня также уве­ли­чи­ва­ет­ся (Г — 1).

Ответ: 2321

14. Гиря мас­сой 2 кг под­ве­ше­на на тон­ком шнуре. Если её от­кло­нить от по­ло­же­ния рав­но­ве­сия на 10 см, а затем от­пу­стить, она со­вер­ша­ет сво­бод­ные ко­ле­ба­ния как ма­те­ма­ти­че­ский ма­ят­ник. Что про­изойдёт с пе­ри­о­дом ко­ле­ба­ний гири, мак­си­маль­ной по­тен­ци­аль­ной энер­ги­ей гири и ча­сто­той её ко­ле­ба­ний, если на­чаль­ное от­кло­не­ние гири будет равно 5 см?

К каж­дой по­зи­ции пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щую по­зи­цию вто­ро­го и за­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ИЗ­МЕ­НЕ­НИЯ
А) Пе­ри­од Б) Ча­сто­та В) Мак­си­маль­ная по­тен­ци­аль­ная энер­гия гири		1) Уве­ли­чит­ся 2) Умень­шит­ся 3) Не из­ме­нит­ся

 

A	Б	В

За­да­ние 7 № 3169

Ре­ше­ние.

Пе­ри­од сво­бод­ных ко­ле­ба­ний ма­те­ма­ти­че­ско­го ма­ят­ни­ка за­ви­сит толь­ко от длины нити и ве­ли­чи­ны уско­ре­ния сво­бод­но­го па­де­ния: 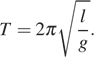Сле­до­ва­тель­но, при умень­ше­нии на­чаль­но­го от­кло­не­ния гири в два раза, пе­ри­од не из­ме­нит­ся (А — 3). Ча­сто­та об­рат­но про­пор­ци­о­наль­на пе­ри­о­ду, зна­чит, ча­сто­та также не из­ме­нит­ся (Б — 3). С дру­гой сто­ро­ны, чем боль­ше на­чаль­ное от­кло­не­ние гири, тем выше она на­хо­дит­ся над по­ло­же­ни­ем рав­но­ве­сия в мо­мен­ты мак­си­маль­но­го от­кло­не­ния. Таким об­ра­зом, при умень­ше­нии на­чаль­но­го от­кло­не­ния гири ее мак­си­маль­ная по­тен­ци­аль­ная энер­гия умень­шит­ся (В — 2).

Ответ: 332

15. Ка­мень сво­бод­но па­да­ет вер­ти­каль­но вниз. Из­ме­ня­ют­ся ли пе­ре­чис­лен­ные в пер­вом столб­це фи­зи­че­ские ве­ли­чи­ны во время его дви­же­ния вниз и если из­ме­ня­ют­ся, то как? Уста­но­ви­те со­от­вет­ствие между фи­зи­че­ски­ми ве­ли­чи­на­ми, пе­ре­чис­лен­ны­ми в пер­вом столб­це, и воз­мож­ны­ми ви­да­ми их из­ме­не­ний, пе­ре­чис­лен­ны­ми во вто­ром столб­це. Вли­я­ни­ем со­про­тив­ле­ния воз­ду­ха пре­не­бречь.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ИЗ­МЕ­НЕ­НИЯ
А) Ско­рость Б) Уско­ре­ние В) Ки­не­ти­че­ская энер­гия Г) По­тен­ци­аль­ная энер­гия		1) Уве­ли­чит­ся 2) Умень­шит­ся 3) Не из­ме­нит­ся

 

A	Б	В	Г

За­да­ние 7 № 3170

Ре­ше­ние.

Пре­не­бре­гая силой со­про­тив­ле­ния воз­ду­ха, за­клю­ча­ем, что на ка­мень дей­ству­ет толь­ко сила тя­же­сти, ко­то­рая со­об­ща­ет ему по­сто­ян­ное уско­ре­ние сво­бод­но­го па­де­ния (Б — 3), на­прав­лен­ное вниз. По­сколь­ку при па­де­нии камня вер­ти­каль­но вниз уско­ре­ние и ско­рость камня со­на­прав­ле­ны, ско­рость камня уве­ли­чи­ва­ет­ся (А — 1). Сле­до­ва­тель­но, ки­не­ти­че­ская энер­гия, про­пор­ци­о­наль­ная квад­ра­ту ско­ро­сти, также уве­ли­чи­ва­ет­ся (В — 1). При дви­же­нии камня вниз его вы­со­та над по­верх­но­стью земли умень­ша­ет­ся, от­сю­да за­клю­ча­ем, что по­тен­ци­аль­ная энер­гия камня также умень­ша­ет­ся (Г — 2).

Ответ: 1312

16. Люст­ра под­ве­ше­на к по­тол­ку на крюч­ке. Уста­но­ви­те со­от­вет­ствие между си­ла­ми, пе­ре­чис­лен­ны­ми в пер­вом столб­це, и их харак­те­ри­сти­ка­ми, пе­ре­чис­лен­ны­ми во вто­ром столб­це. За­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ХА­РАК­ТЕ­РИ­СТИ­КИ
А) Сила тя­же­сти люст­ры Б) Сила веса люст­ры		1) При­ло­же­на к люст­ре и на­прав­ле­на вер­ти­каль­но вниз 2) При­ло­же­на к крюч­ку и на­прав­ле­на вер­ти­каль­но вверх 3) При­ло­же­на к крюч­ку и на­прав­ле­на вер­ти­каль­но вниз 4) При­ло­же­на к люст­ре и на­прав­ле­на вер­ти­каль­но вверх

 

A	Б

За­да­ние 7 № 3171

Ре­ше­ние.

Сила тя­же­сти — это сила, с ко­то­рой Земля при­тя­ги­ва­ет тело, она при­ло­же­на к са­мо­му телу. Сле­до­ва­тель­но, сила тя­же­сти люст­ры при­ло­же­на к люст­ре и на­прав­ле­на вер­ти­каль­но вниз (А — 1). Вес тела — это сила, с ко­то­рой тело давит на опору, либо рас­тя­ги­ва­ет под­вес, эта сила при­ло­же­на к опоре. Таким об­ра­зом, сила веса люст­ры при­ло­же­на к крюч­ку и на­прав­ле­на вер­ти­каль­но вниз (Б — 3).

Ответ: 13

17. Че­ло­век сидит на стуле. Уста­но­ви­те со­от­вет­ствие между си­ла­ми, пе­ре­чис­лен­ны­ми в пер­вом столб­це, и их ха­рак­те­ри­сти­ка­ми, пе­ре­чис­лен­ны­ми во вто­ром столб­це. За­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ФИ­ЗИ­ЧЕ­СКИЕ ВЕ­ЛИ­ЧИ­НЫ		ИХ ХА­РАК­ТЕ­РИ­СТИ­КИ
А) Сила тя­же­сти че­ло­ве­ка Б) Сила веса че­ло­ве­ка на стул		1) При­ло­же­на к че­ло­ве­ку и на­прав­ле­на вер­ти­каль­но вниз 2) При­ло­же­на к че­ло­ве­ку и на­прав­ле­на вер­ти­каль­но вверх 3) При­ло­же­на к стулу и на­прав­ле­на вер­ти­каль­но вниз 4) При­ло­же­на к стулу и на­прав­ле­на вер­ти­каль­но вверх

 

A	Б

За­да­ние 7 № 3173

Ре­ше­ние.

Сила тя­же­сти — это сила, с ко­то­рой Земля при­тя­ги­ва­ет тело, она при­ло­же­на к са­мо­му телу. Сле­до­ва­тель­но, сила тя­же­сти че­ло­ве­ка при­ло­же­на к че­ло­ве­ку и на­прав­ле­на вер­ти­каль­но вниз (А — 1). Вес тела — это сила, с ко­то­рой тело давит на опору, либо рас­тя­ги­ва­ет под­вес, эта сила при­ло­же­на к опоре. Таким об­ра­зом, сила веса че­ло­ве­ка при­ло­же­на к стулу и на­прав­ле­на вер­ти­каль­но вниз (Б — 3).

Ответ: 13

18. Бру­сок дви­жет­ся рав­но­мер­но по го­ри­зон­таль­ной по­верх­но­сти. Уста­но­ви­те для силы тре­ния со­от­вет­ствие па­ра­мет­ров силы, пе­ре­чис­лен­ных в пер­вом столб­це, со свой­ства­ми век­то­ра силы, пе­ре­чис­лен­ны­ми во вто­ром столб­це. За­пи­ши­те в таб­ли­цу вы­бран­ные цифры под со­от­вет­ству­ю­щи­ми бук­ва­ми.

 

ПА­РА­МЕТ­РЫ СИЛЫ		СВОЙ­СТВА ВЕК­ТО­РА СИЛЫ
А) На­прав­ле­ние век­то­ра Б) Мо­дуль век­то­ра		1) Вер­ти­каль­но вниз 2) Про­тив на­прав­ле­ния век­то­ра ско­ро­сти 3) Вер­ти­каль­но вверх 4) Про­пор­ци­о­на­лен силе нор­маль­но­го дав­ле­ния и об­рат­но про­пор­ци­о­на­лен пло­ща­ди по­верх­но­сти брус­ка 5) Об­рат­но про­пор­ци­о­на­лен силе нор­маль­но­го дав­ле­ния и об­рат­но про­пор­ци­о­на­лен пло­ща­ди по­верх­но­сти брус­ка 6) Про­пор­ци­о­на­лен силе нор­маль­но­го дав­ле­ния и не за­ви­сит от пло­ща­ди по­верх­но­сти брус­ка 7) Об­рат­но про­пор­ци­о­на­лен силе нор­маль­но­го дав­ле­ния и про­пор­ци­о­на­лен пло­ща­ди по­верх­но­сти брус­ка 8) Про­пор­ци­о­на­лен силе нор­маль­но­го дав­ле­ния и про­пор­ци­о­на­лен пло­ща­ди по­верх­но­сти

 

A	Б

За­да­ние 7 № 3180

Ре­ше­ние.

Сила тре­ния все­гда на­прав­ле­на про­тив ско­ро­сти от­но­си­тель­но­го дви­же­ния тел (А — 2). Экс­пе­ри­мен­таль­ным фак­том яв­ля­ет­ся то, что ве­ли­чи­на силы тре­ния не за­ви­сит от пло­ща­ди по­верх­но­сти брус­ка. Бру­сок дви­жет­ся, сле­до­ва­тель­но, сила тре­ния пред­став­ля­ет собой силу тре­ния сколь­же­ния, а зна­чит, она про­пор­ци­о­наль­на силе нор­маль­но­го дав­ле­ния: . В итоге, (Б — 6).

Ответ: 26

19. Бру­сок сколь­зит по на­клон­ной плос­ко­сти вниз без тре­ния. Что про­ис­хо­дит при этом с его ско­ро­стью, по­тен­ци­аль­ной энер­ги­ей, силой ре­ак­ции на­клон­ной плос­ко­сти? Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

1. уве­ли­чи­лась;

2. умень­ши­лась;

3. не из­ме­ни­лась.

 

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

 

Ско­рость брус­ка	По­тен­ци­аль­ная энер­гия брус­ка	Сила ре­ак­ции на­клон­ной плос­ко­сти

За­да­ние 7 № 3195

Ре­ше­ние.

Вы­со­та брус­ка над зем­лей умень­ша­ет­ся при его дви­же­нии вниз вдоль на­клон­ной плос­ко­сти, а зна­чит, его по­тен­ци­аль­ная энер­гия умень­ша­ет­ся. По­сколь­ку бру­сок сколь­зит по на­клон­ной плос­ко­сти без тре­ния, для него вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской э

Поделиться:

Воспользуйтесь поиском по сайту: