Отсюда согласно (12’) получаем

Решение рекуррентного соотношения (11) суть

В монографии [9] (с. 66) приведено рекуррентное соотношение, являющееся обобщением (11), и определено его решение.

ФОРМУЛА ВКЛЮЧЕНИЙ И ИСКЛЮЧЕНИЙ

Здесь мы введем важную комбинаторную формулу, которой озаглавлен этот параграф.

Пусть – некоторые конечные множества и для каждого из этих i выполнено включение: . Напомним, что есть мощность конечного множества .

Убедимся, что верна следующая формула

.

(12)

В самом деле, каждый элемент из в левой части равенства (12) учитывается один раз. В правой же части этого равенства он учитывается в или , и если он входит в , то учитывается дважды; поэтому двойное учитывание исключается присутствием сле-дующего члена: 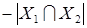. (Заметим, что в этом простом рассуждении процесс состоял во включении “всех” и исключении “лишнего”.)

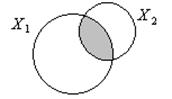
При изображении кругами Эйлера элементы двойного учитывания заштрихованы; именно они составляют :

 

Когда , т. е. , то согласно равенству (12) получаем:

.

(12’)

Теперь, исходя из равенств (12) и (12’), найдем мощность множества . Очевидно имеем

,

.

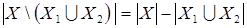Тогда согласно равенству (12’) получаем, что , откуда . Откуда согласно равенству (12) имеем

.

(13)

Придадим равенству (13) следующий смысл. Пусть Х есть множество элементов, каждый из которых может обладать либо свойством , либо свойством и . Далее, пусть есть множество всех элементов из Х, которые обладают свойством и , а 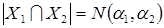. Тогда есть подмножество всех тех элементов из Х, которые не обладают ни ни , и пусть . Следовательно, в таком случае равенство (13) перепишется следующим образом:

.

(14)

Формула (14) есть частный случай формулы включений и исключений, общий вид которой мы напишем после следующих обозначений.

Пусть имеется множество Х из N элементов, обладающих n свойствами 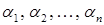; каждый элемент из Х может либо не обладать ни одним из указанных свойств, либо обладать одним или несколькими свойствами. Обозначим через количество элементов, обладающих свойствами (и, быть может, некоторыми другими свойствами). Число элементов, не обладающих ни одним из указанных свойств, обозначим через . Тогда общий вид формулы включений и исключений

(15)

В формуле (15) алгебраическая сумма распространена на все сочетания свойств из n -множества , причем знак “+” ставится, если число учитываемых свойств четно, и знак “-”, если такое число нечетно; как будет указано ниже, правая часть этой формулы содержит алгебраических слагаемых.

Доказательство формулы (15) можно провести следующим образом.

Действовать будем аналогично тому, как мы доказали формулу (14).

Убедимся методом математической индукции по n, что для любых конечных множеств верно равенство

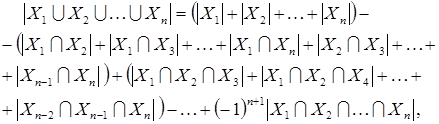
(16)

в правой части которого имеется алгебраических слагаемых.

Формулу (16) запишем в более компактном виде следующим образом:

(16’)

Базис индукции: n =2 верен согласно формуле (12), в правой части которой имеется алгебраических слагаемых.

Предположим, что равенство (16) верно для случая n -1 подмножеств, где , и в правой его части будет 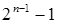слагаемых.

Докажем ее для n подмножеств. Разобъем множества на две системы , . Согласно формуле (12) имеем

(17)

Согласно индуктивному предположению имеем (используем (16’)):

а)

.

b)

,

где в каждой из этих формул в правой части имеется по 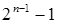алгебраических слагаемых.

Подставляя в (17) формулы, полученные в пп. а) и b), получаем (16). Осталось подсчитать число слагаемых в (16). В формуле (17) имеется 3 слагаемых, но вместо 1-го и 3-го подставляются по 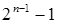слагаемых; следовательно, всех слагаемых в (16) будет .

Теперь пусть каждое из рассмотренных множеств является подмножеством множества Х, т. е. .

Тогда ,

а .

Отсюда согласно (12’) получаем

,

откуда .

Используя в последнем равенстве формулу (16) и интерпретацию, аналогичную той, которую мы применили к равенству (13), получаем формулу (15). Заметим, что в формуле (15) имеется в правой части ровно алгебраических слагаемых.

Примеры.

1. Было опрошено 70 человек. В результате опроса выяснили, что 59 человек знают английский язык, 31 – немецкий, 45 – французский,
25 – английский и немецкий, 30 – английский и французский, 25 – немецкий и французский, а 11 человек – все три языка. Сколько человек из опрошенных не знают ни одного языка?

По формуле (15) при получаем

2. В ряде случаев формулу (15) можно использовать для того, чтобы показать, что решения комбинаторной задачи не существует.

Например, староста одного класса дал следующие сведения об учениках: “В классе учатся 45 учащихся, в том числе 25 мальчиков. Спортом занимаются 28 учеников, из них 18 мальчиков и 17 хорошо успевающих школьников, 15 мальчиков в классе учатся хорошо и в то же время занимаются спортом”.

Выясним, являются ли эти сведения совместимыми. Обозначим через принадлежность к мужскому полу, через – хорошую успеваемость и через – увлечение спортом. По условию задачи

Тогда есть число слабо успевающих девочек, не занимающихся спортом. По формуле (15) получаем

.

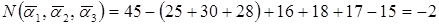Но отрицательным ответ быть не может. Значит, данные сведения противоречивы.

Рассмотрим частный случай формулы (15), когда число элементов, обладающих свойствами , не зависит от самих свойств, а только зависит от их числа. Таким образом, пусть

и т. д.

Тогда в сумме , полагая , получаем, что

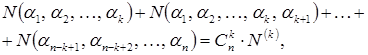
потому что в левой части сумма берется по всем возможным сочетаниям k свойств из n свойств. Следовательно, в рассмотренном случае формула (15) принимает вид

.

(18)

Пример 3. Найти число 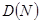перестановок 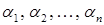из n элементов , в которых для каждого 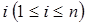выполнено , т. е. ни один элемент не остается на месте. Ясно, что в этом случае будет применима формула (18), ибо все элементы равноправны. Здесь через обозначим количество перестановок, в которых заданные k чисел остались на своих местах, 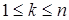. Но если k чисел остались на своих местах, то в таких перестановках остальныые чисел будут занимать любые места, что дает случаев. Значит,

т. е. .

Очевидно, что фигурирующая здесь сумма есть частная сумма разложения .

 

2.11. ПРОИЗВОДЯЩИЕ ФУНКЦИИ

Одним из наиболее эффективных средств решения перечислительных комбинаторных задач является метод производящих функций. Основная идея этого метода состоит в сопоставлении каждой числовой последовательности функции действительного (или комплексного) переменного, причем отношения между последовательностями отражаются в отношениях между функциями. К самим функциям применимы аналитические методы исследования, которые иногда оказываются более простыми и удобными, чем непосредственное оперирование с числовыми последовательностями.

Вместо будем писать .

Поделиться:

Воспользуйтесь поиском по сайту: