 |
Инструкция по выполнению работы
|
|
|
|
Работа состоит из трех модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 26 заданий. Модуль «Алгебра» содержит 11 заданий: в части 1 - восемь заданий; в части 2 – три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 – пять заданий; в части 2 – три задания. Модуль «Реальная математика» содержит семь заданий: все задания этого модуля - в части 1.
На выполнение работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 2, 3, 8, 14 записываются в виде однойили нескольких цифр, которые соответствуют номеру правильного ответа. Эти цифры запишите в поле ответа в тексте работы без пробелов и запятых.
Для остальных зданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите ее в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.
Решение заданий части 2 и ответы к ним запишите на отдельном листе или бланке. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо указать только его номер.
Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы. Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
|
|
|
При выполнении работы Вы можете воспользоваться справочными материалами.
Баллы, полученные за верно выполненные задания, суммируются. Для успешного выполнения работы необходимо набрать в сумме не менее 8 баллов, из них не менее 3 баллов в модуле «Алгебра», не менее 2 баллов в модуле «Геометрия» и не менее 2 баллов в модуле «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания оцениваются в 2 балла.
Желаем успеха!
| Часть 1 | ||||||||||||||||||||
| Модуль «Алгебра» | ||||||||||||||||||||
Найдите значение выражения 
| ||||||||||||||||||||
| Ответ:___________________________________ | ||||||||||||||||||||
На координатной прямой отмечено число с. Расположите в порядке убывания числа с, с2, 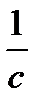
| ||||||||||||||||||||
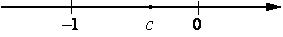
| ||||||||||||||||||||
| Ответ: | ||||||||||||||||||||
Найти значение выражения 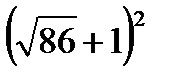 .
1) .
1)  2) 85
3)
2) 85
3) 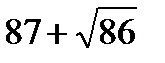 4)
4) 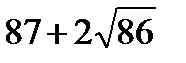
| ||||||||||||||||||||
| Ответ: | ||||||||||||||||||||
| Найдите корень уравнения – 3x2+ 2x +6 = – х2 + 3 – (− 3 + 2x2). | ||||||||||||||||||||
| Ответ:________________________ | ||||||||||||||||||||
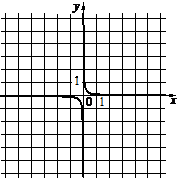
Установите соответствие между функциями и их графиками
ФУНКЦИИ
| ||||||||||||||||||||
ГРАФИКИ
| ||||||||||||||||||||
В таблице под каждой буквой укажите соответствующий номер
| ||||||||||||||||||||
Найдите значение выражения  при при 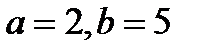
| ||||||||||||||||||||
| Ответ:________________________ | ||||||||||||||||||||
Сократите дробь  . .
| ||||||||||||||||||||
| Ответ:________________________ | ||||||||||||||||||||
| Укажите неравенство, решением которого является любое число. | ||||||||||||||||||||
| ||||||||||||||||||||
| Ответ: | ||||||||||||||||||||
| Модуль «Геометрия» | ||||||||||||||||||||
| Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 19°. Найдите величину угла OMK. Ответ дайте в градусах. | ||||||||||||||||||||
 Ответ:______________________________
Ответ:______________________________
| ||||||||||||||||||||
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48.

| ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

| ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
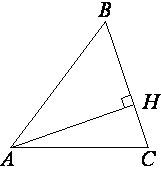
В остроугольном треугольнике ABC высота AH равна 13  , а сторона AB равна 52. Найдите cosB. , а сторона AB равна 52. Найдите cosB.
| ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
| Какое из следующих утверждений верно? 1) Если диагонали параллелограмма равны, то этот параллелограмм является квадратом. 2) Сумма углов равнобедренного треугольника равна 180 градусам. 3) Площадь трапеции равна произведению основания трапеции на высоту. | ||||||||||||||||||||
| В ответ запишите номер выбранного утверждения. Ответ:______________________________ | ||||||||||||||||||||
| Модуль «Реальная математика» | ||||||||||||||||||||
В таблице приведены нормативы по прыжкам с места для учащихся 11 класса.
Какую отметку получит девочка, прыгнувшая на 167 см? | ||||||||||||||||||||
| ||||||||||||||||||||
| Ответ: | ||||||||||||||||||||
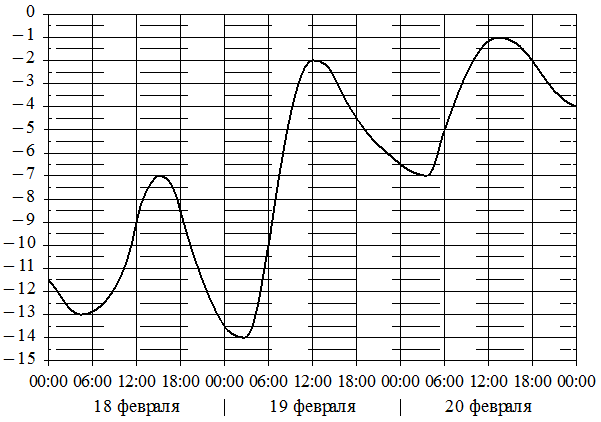
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали - значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
| ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
| Набор полотенец, который стоил 200 рублей, продаётся с 3-процентной скидкой. При покупке этого набора покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить? | ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
| Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м? | ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
В городе из учебных заведений имеются школы, колледжи, училища и институты. Данные представлены на круговой диаграмме.
 Какие из утверждений относительно количества учебных заведений разных видов неверны, если всего в городе 30 учебных заведений?
Какие из утверждений относительно количества учебных заведений разных видов неверны, если всего в городе 30 учебных заведений?
| ||||||||||||||||||||
В ответе запишите номера выбранных утверждений.
| ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
Ответ:______________________________
| ||||||||||||||||||||
| Расстояние s (в метрах) до места удара молнии можно приближенно вычислить по формуле s=330t, где t – количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t=9 с. Ответ дайте в километрах, округлив его до целых. | ||||||||||||||||||||
| Ответ:______________________________ | ||||||||||||||||||||
| Часть 2 | ||||||||||||||||||||
| Модуль «Алгебра» | ||||||||||||||||||||
Решите уравнение 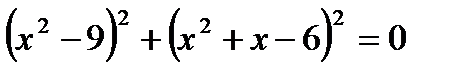 . .
| ||||||||||||||||||||
| Расстояние между пристанями А и В равно 75 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 44 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. | ||||||||||||||||||||
| При каком значении р прямая y =− x + p имеет с параболой y = x 2+3 x ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p. | ||||||||||||||||||||
| Модуль «Геометрия» | ||||||||||||||||||||
На стороне BC прямоугольника ABCD, у которого AB=10 и AD=34, отмечена точка E так, что ∠EAB=45°. Найдите ED.

| ||||||||||||||||||||
| В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник. | ||||||||||||||||||||
| Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16. |
|
|
|
|
|
|



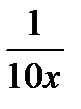



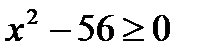
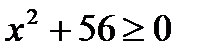

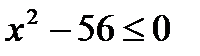
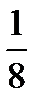 всех учебных заведений - институты.
всех учебных заведений - институты.