 |
Квадратные уравнения частного характера
|
|
|
|
Введение
В данной статье я привожу методы решения квадратных уравнений. Систематизированы и даны методы решения основных видов квадратных уравнений. Данная статья облегчает учащимся лучше понять данную тему и наработать навыки решения квадратных уравнений любых сложностей.
x2 + 4x + 12 = 0 Это квадратное уравнение называют не приведенным, если старший коэффициент отличен от 1.
2x2 + 6x + 3 = 0 это полное квадратное уравнение - в котором присутствуют все три слагаемых, это уравнение, у которого коэффициенты b и c не равны нулю.
3x2 + 4x + 2 = 0 Неполное квадратное уравнение – это квадратное уравнение, у которого хотя бы один коэффициент b, c равен нулю.
Таким образом, выделяют три вида неполных квадратных уравнений:
1) ax² = 0 (имеет два совпадающих корня x = 0).
2) ax² + bx = 0 (имеет два корня x1 = 0 и x2 = - 
)
Задача(1): x2 + 2x = 0
x(x+2) =0
x1= 0, x2 = -2.
Ответ: x1=0, x2= -5.
3) ax² + c = 0
Если – 
<0 - уравнение не имеет корней.
Задача(2): 2x2 + 7 = 0
Ответ: уравнение не имеет корней.
Если – > 0, то x1,2 = ±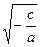 
Задача(3): 2x2 – 8 = 0
х2=± 
х1,2=± 
Ответ: х1,2=±
Любое квадратное уравнение можно решить через дискриминант (b² - 4ac).
Задача(4): х2 +14x – 23 = 0
D = b2 – 4ac = 144 + 92 = 256
x1,2 =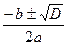 
x1 = 
x2 = 
Ответ: x1 = 1, x2 = - 15.
Дискриминант имеет три правила
1) Если D < 0, то не имеет решения.
2) Если D = 0, то уравнение имеет два совпадающих решения
3) Если D > 0, то имеет два решения, находящиеся по формуле:
Теорема Виета
Чтобы числа x1 и x2 являлись корнями уравнения: ax² + bx + c = 0 необходимо и достаточно выполнения равенства x1 + x2 = -b/a и x1x2 = c/a
Теорема Виета позволяет судить о знаках и абсолютной величине квадратного уравнения
1. Если b>0, c>0 то оба корня отрицательны.
2. Если b<0, c>0 то оба корня положительны.
|
|
|
3. Если b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.
4. Если b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.
Квадратные уравнения частного характера
1) Если a + b + c = 0 в уравнении ax² + bx + c = 0, то
х1=1, а х2 = .
Доказательство:
В уравнении ax² + bx + c = 0, его корни
x1,2 = 
(1).
Представим b из равенства a + b + c = 0
Подставим это выражение в формулу (1):
х1,2= 
= 
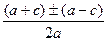
Если рассмотрим по отдельности два корня уравнения, получим:
1) х1= 
2) х2= 
Отсюда следует: х1=1, а х2 = .
Задача(1): 2х² - 3х + 1 = 0
a = 2, b = -3, c = 1.
a + b + c = 0, следовательно
х1 = 1
х2 = ½
Задача(2): 418х² - 1254х + 836 = 0
Этот пример очень тяжело решить через дискриминант, но, зная выше приведенную формулу его с легкостью можно решить.
a = 418, b = -1254, c = 836.
х1 = 1 х2 = 2
2) Если a - b + c = 0, в уравнении ax² + bx + c = 0, то:
х1=-1, а х2 =- .
Доказательство:
Рассмотрим уравнение ax² + bx + c = 0, из него следует, что:
x1,2 = (2).
Представим b из равенства a - b + c = 0
b = a + c, подставим в формулу (2):
x1,2= 
= 
Получаем два выражения:
1) х1= 
2) х2=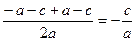 
Эта формула похожа на предыдущую, но она тоже важна, т.к. часто встречаются примеры такого типа.
Задача(3): 2х² + 3х + 1 = 0
a = 2, b = 3, c = 1.
a - b + c = 0, следовательно
х1 = -1
х2 = -1/2
Задача(4):
Задача(5): x1 = -1; х2 = - 
Метод “ переброски ”
Корни квадратных уравнений y² + by + аc = 0 и ax² + bx + c = 0 связанны соотношениями:
х1 =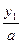 
и х2 = 
Доказательство:
а) Рассмотрим уравнение ax² + bx + c = 0
x1,2 = = 
б) Рассмотрим уравнение y² + by + аc = 0
y1,2 =
Заметим, что дискриминанты у обоих решений равны, сравним корни этих двух уравнений. Они отличаются друг от друга на старший коэффициент, корни первого уравнения меньше корней второго на а. Используя теорему Виета и выше приведенное правило, нетрудно решать разнообразные уравнения.
Имеем произвольное квадратное уравнение
|
|
|
10х² - 11х + 3 = 0
Преобразуем это уравнение по приведенному правилу
y² - 11y + 30 = 0
Получим приведенное квадратное уравнение, которое можно достаточно легко решить с помощью теоремы Виета.
Пусть y1 и y2 корни уравнения y² - 11y + 30 = 0
y1y2 = 30 y1 = 6
y1 + y2 = 11 y2 = 5
Зная, что корни этих уравнений отличны друг от друга на а, то
х1 = 6/10 = 0,6
х2 = 5/10 = 0,5
В некоторых случаях удобно решать сначала не данное уравнение ax² + bx + c = 0, а приведенное y² + by + аc = 0, которое получается из данного «переброской» коэффициента а, а затем разделить найденный корни на а для нахождения исходного уравнения.
Программа
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
cout << "Input a, b, c: ";
double a, b, c;
cin >> a >> b >> c; cin.get();
double d = b*b - 4*a*c;
cout << "d = " << d << endl;
if (d > 0)
{
double x1 = (-b - d) /2 /a;
double x2 = (-b + d) /2 /a;
cout << "x1 = " << x1 << '\t';
cout << "x2 = " << x2 << endl;
}
else if (d == 0)
{
double x = (-b) /2 /a;
cout << "x = " << x << endl;
}
else if (d < 0)
{
cout << "There are o real roots." << endl;
}
else
{
cerr << "Unexpected 'd' value." << endl;
//TODO: throw an exception
}
cout << "Thank you for using our product! See more at " << /* your website here */ "example.com" << endl;
cin.get();
}
Заключение
В этой статье мы узнали, что такое квадратные уравнения, методы решения квадратных уравнений и закрепили все теоретические знания примерами решения задач.
Список литературы
|
|
|
