 |
Московский государственный университет
|
|
|
|
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Кафедра «Экономические информационные системы»
УТВЕРЖДАЮ
Заведующий кафедрой ЭФ-2
_________________ Лагунова А.Д.
«____»_____________2012г.
Для студентов факультета ЭФ
специальности 080801
к.т.н., профессор Дмитриев Я.В., к.т.н. Зуев А.С.
(ученая степень, ученое звание, фамилия и инициалы автора)
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
(Методические рекомендации)
ДЛЯ ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ № 3
По дисциплине «Эконометрика»
ТЕМА « Решение задач по корреляционному и дисперсионному анализу »
Обсуждена на заседании кафедры
(предметно-методической секции)
«15»мая 2012 г.
Протокол № 11
МГУПИ – 2012 г.
1. Тема практического занятия № 3: решение задач по корреляционному и дисперсионному анализу.
2. Учебные и воспитательные цели:
1. Выработать практические умения, а также приобрести навыки решения задач по парному корреляционному анализу.
2. Выработать практические умения, а также приобрести навыки решения задач по множественному корреляционному анализу.
3. Выработать практические умения, а также приобрести навыки решения задач по дисперсионному анализу.
3. Время: 2 часа (90 минут).
4. Место проведения: специализированная аудитория.
5. Литература для подготовки (основная и дополнительная):
а) Основная литература:
1. Федосеев В.В., Гармаш А.Н., Орлова И.В. и др. / Экономико-математические методы и прикладные модели: Учебное пособие для вузов / Москва / ЮНИТИ-ДАНА / 2012
2. Васильева Э.К., Лялин В.С. / Статистика: Учебник для студентов вузов, обучающихся по специальностям экономики и управления (080100) / Москва / ЮНИТИ-ДАНА / 2012
|
|
|
3. Буравлев А.И. Эконометрика: доп. УМО в кач. учеб. пособия для вузов. — М.: Бином. Лаборатория знаний, 2012
б) Дополнительная литература:
1. Колемаев В.А., Гатауллин Т.М., Заичкин Н.И. и др. / Математические методы и модели исследования операций: Учебник для студентов вузов, обучающихся по специальности 080116 «Математические методы в экономике» и другим экономическим специальностям / Москва / ЮНИТИ-ДАНА / 2012
2. Балдин К.В., Башлыков В.Н., Рукосуев А.В. / Основы теории вероятностей и математической статистики: Учебник / Москва / Флинта / 2010
6. РАСЧЕТ УЧЕБНОГО ВРЕМЕНИ:
Вступительная часть — до 10 минут (напомнить содержательные постановки задач применения методов корреляционного и дисперсионного анализа).
Основная часть (учебные вопросы) — до 80 мин.
1-й учебный вопрос: решение задач по парному корреляционному анализу — 20 минут.
2-й учебный вопрос: решение задач по множественному корреляционному анализу — 20 минут.
3-й учебный вопрос: решение задач по дисперсионному анализу — 40 минут.
Заключительная часть — до 5 минут.
С О Д Е Р Ж А Н И Е
| Содержание занятия (указания и рекомендации по методике проведения) | Время (в мин.) |
| Вступительная часть: - проверить наличие студентов по докладу старосты; - проверить наличие журнала группы, правильность записи темы занятия, отметить отсутствующих, поставить свою подпись; - раскрыть содержание ПЗ; - довести целевую установку через учебные вопросы ПЗ; - вскрыть особенности практической работы студентов на ПЗ. | До 10 |
| Основная часть — рассмотрение учебных вопросов: (в процессе выполнения работы отвечать на индивидуальные вопросы студентов с целью разъяснения вызвавших затруднения моментов) 1-й учебный вопрос:решение задач по парному корреляционному анализу — 20 минут. 2-й учебный вопрос: решение задач по множественному корреляционному анализу — 20 минут. 3-й учебный вопрос: решение задач по дисперсионному анализу — 40 минут. Заключительная часть: - подведение итогов занятия; - оценить учебную деятельность студентов; - собрать файлы с решениями примеров; - ответить на вопросы студентов. | До 80 До 5 |
8. Приложения: приведенный далее текст с материалами распечатки содержания практического занятия и состава вариантов.
|
|
|
1-й учебный вопрос: решение задач по парному корреляционному анализу.
Коэффициент корреляции симметричен, т.е. не изменяется, если X и Y поменять местами

| x | y | x 2 | y 2 | x • y | y(x) | (yi-ycp) 2 | (y-y(x))2 | (xi-xcp)2 | |y - yx|:y |
| 68.5 | 22.39 | 4692.25 | 501.31 | 1533.72 | 29.06 | 63.49 | 44.44 | 71.33 | 0.3 |
| 75.7 | 29.24 | 5730.49 | 854.98 | 2213.47 | 27.95 | 1.25 | 1.67 | 244.78 | 0.0442 |
| 52.7 | 32.92 | 2777.29 | 1083.73 | 1734.88 | 31.49 | 6.56 | 2.04 | 54.09 | 0.0434 |
| 60.2 | 33.52 | 3624.04 | 1123.59 | 2017.9 | 30.34 | 10.14 | 0.0212 | 0.095 | |
| 62.3 | 30.98 | 3881.29 | 959.76 | 1930.05 | 30.01 | 0.39 | 0.94 | 5.04 | 0.0312 |
| 48.3 | 37.17 | 2332.89 | 1381.61 | 1795.31 | 32.17 | 46.4 | 138.17 | 0.13 | |
| 56.5 | 32.12 | 3192.25 | 1031.69 | 1814.78 | 30.91 | 3.1 | 1.47 | 12.63 | 0.0378 |
| 65.9 | 31.76 | 4342.81 | 1008.7 | 2092.98 | 29.46 | 1.97 | 5.3 | 34.17 | 0.0725 |
| 56.2 | 28.48 | 3158.44 | 811.11 | 1600.58 | 30.95 | 3.53 | 6.11 | 14.86 | 0.0868 |
| 51.1 | 23.17 | 2611.21 | 536.85 | 1183.99 | 31.74 | 51.67 | 73.42 | 80.18 | 0.37 |
| 63.2 | 32.19 | 3994.24 | 1036.2 | 2034.41 | 29.87 | 3.36 | 5.37 | 9.89 | 0.072 |
| 660.6 | 333.94 | 40337.2 | 10329.52 | 19952.07 | 333.94 | 191.71 | 175.9 | 665.17 | 1.29 |
1. Расчет средних значений x,y:

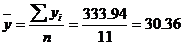

2. Расчет дисперсий:


3. Расчет среднеквадратических отклонений:
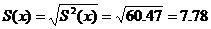

4. Расчет линейного коэффициента корреляции Пирсона:

2-й учебный вопрос: решение задач по множественному корреляционному анализу.



Предположим, 
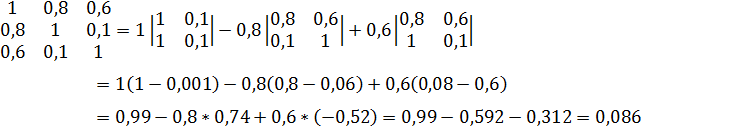


Предположим, 

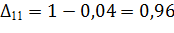

Предположим, 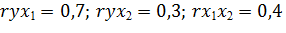

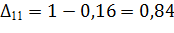

3-й учебный вопрос: решение задач по дисперсионному анализу.
Рассмотрим выборочное обследование производительности труда рабочих одинаковых профессий на четырех однотипных заводах разных городов. Производительность выражена в относительных величинах по отношению к базовой, принятой за единицу. Требуется установить, существенно различаются производительности труда рабочих рассматриваемых профессий на четырех заводах. Исходные данные приведены в таблице. Принять уровень значимости, равным 0,05.
| Порядковый номер | Заводы | |||
| 1,55 | 1,62 | 1,69 | 1,76 | |
| 0,70 | 0,52 | 0,34 | 0,17 | |
| 0,22 | 0,12 | 0,47 | 0,81 | |
| 0,38 | 0,91 | 1,45 | 1,99 | |
| 1,70 | 2,79 | 3,89 | ||
| 2,88 | 4,35 | 5,83 | ||
| 10,73 |
|
|
|
Однофакторный дисперсионный анализ. Это средство служит для анализа дисперсии по данным двух или нескольких выборок. При анализе сравнивается гипотеза о том, что каждый пример извлечен из одного и того же базового распределения вероятности, с альтернативной гипотезой, предполагающей, что базовые распределения вероятности во всех выборках разные.
Таким образом, процедура однофакторного дисперсионного анализа состоит в проверке гипотезы H0 о том, что имеется одна группа однородных экспериментальных данных против альтернативы о том, что таких групп больше, чем одна. Под однородностью понимается одинаковость средних значений и дисперсий в любом подмножестве данных. При этом дисперсии могут быть как известны, так и неизвестны заранее. Если имеются основания полагать, что известная или неизвестная дисперсия измерений одинакова по всей совокупности данных, то задача однофакторного дисперсионного анализа сводится к исследованию значимости различия средних в группах данных.
| Группы | Счет | ∑ | Среднее | Дисперсия | ∑² |
| Завод 1 | 18,148 | 2,592571429 | 13,71859262 | 47,04999 | |
| Завод 2 | 10,317 | 1,7195 | 2,5430923 | 17,74008 | |
| Завод 3 | 13,66 | 2,276666667 | 4,643834267 | 31,09927 | |
| Завод 4 | 4,723 | 1,18075 | 0,71674825 | 5,576682 | |
| Итого: | (S1) 46,848 | - | - | (S2) 101,47 |
Счет - кол-во выборок по каждому заводу
S1 - сумма выборок по каждому заводу, пример:
S1 ( Завод 1) = 1,55 + 0,70 + 0,22 + 0,38 + 1,70 + 2,88 + 10,73 = 18,148
Среднее ( Завод 1) = (1,55 + 0,70 + 0,22 + 0,38 + 1,70 + 2,88 + 10,73)/7 = 2,592571429
Дисперсия: 
S2 - сумма выборок в квадрате по каждому заводу, пример:
S1 ( Завод 1) = 1,55 ² + 0,70 ² + 0,22 ² + 0,38 ² + 1,70 ² + 2,88 ² + 10,73 ² = 47,04999
При проведении дисперсионного анализа должны выполняться следующие статистические допущения: независимо от уровня фактора величины отклика имеют нормальный (Гауссовский) закон распределения и одинаковую дисперсию. Такое равенство дисперсий называется гомогенностью. Таким образом, изменение способа обработки сказывается лишь на положении случайной величины отклика, которое характеризуется средним значением или медианой. Поэтому все наблюдения отклика принадлежат сдвиговому семейству нормальных распределений.
|
|
|
Говорят, что техника дисперсионного анализа является "робастной". Этот термин, используемый статистиками, означает, что данные допущения могут быть в некоторой степени нарушены, но несмотря на это, технику можно использовать.
При неизвестном законе распределения величин отклика используют непараметрические (чаще всего ранговые) методы анализа.
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 6,042751311 | 2,014250437 | 0,317872858 | 0,812302731 | 3,127350015 | |
| Внутри групп | 120,3964333 | 6,336654384 | ||||
| Итого | 126,4391846 |
Как видно из таблицы, общая сумма квадратов
SS (Q) = S2 – S1²/n = 101,47 - 46,848 ²/ 23 = 6,042751311= 126,4391846
разбита на компоненты:
Q1, обусловленную различием средних значений между группами
Q1 = (47,04999 ² /7 + 17,74008 ² /6 + 31,09927 ² /6 + 5,576682 ² /4) - 46,848 ²/ 23 = 6,042751311
Q2, обусловленную внутригрупповой изменчивостью
Q2 = Q – Q1 = 126,4391846 - 6,042751311 = 120,3964333
Q= Q 1 +Q 2,
где Q - общая сумма квадратов отклонений наблюдений от общего среднего,
Q 1- сумма квадратов отклонений выборочных средних от общего среднего,
Q 2- сумма квадратов отклонений наблюдений от групповых средних,
Заметим, что MS в этой таблице есть средний квадрат, равный SS, деленная на число степеней свободы (df).
MS1 = Q1/ df1 = 6,042751311 / 3 = 2,014250437
MS2 = Q2/ df2 = 120,3964333 / 19 = 6,336654384
F = MS1 / MS2 = 2,014250437 / 6,336654384 = 0,317872858
Внутригрупповая изменчивость (SS) обычно называется остаточной компонентой или дисперсией ошибки. Это означает, что обычно при проведении эксперимента она не может быть предсказана или объяснена. С другой стороны, SS эффекта (или компоненту дисперсии между группами) можно объяснить различием между средними значениями в группах. Иными словами, принадлежность к некоторой группе объясняет межгрупповую изменчивость, т.к. нам известно, что эти группы обладают разными средними значениями.
Проверка значимости. Основные идеи проверки статистической значимости обсуждаются в разделе Элементарные понятия статистики. В этом же разделе объясняются причины, по которым многие критерии используют отношение объясненной и необъясненной дисперсии. Примером такого использования является сам дисперсионный анализ. Проверка значимости в дисперсионном анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым разбросом (называемой средним квадратом эффекта или MSэффект) и компоненты дисперсии, обусловленной внутригрупповым разбросом (называемой средним квадратом ошибки или MSошибка; эти термины были впервые использованы в работе Edgeworth, 1885). Если верна нулевая гипотеза (равенство средних в двух популяциях), то можно ожидать сравнительно небольшое различие выборочных средних из-за чисто случайной изменчивости. Поэтому, при нулевой гипотезе, внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1. В рассмотренном выше примере F-критерий показывает, что различие между средними статистически значимо.
|
|
|
Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.
Практическое занятие разработано:
к.т.н., профессор Дмитриев Я.В., к.т.н. Зуев А.С.
«___»_________2012 г.
|
|
|


