 |
Прямая линия, принадлежащая плоскости
|
|
|
|
Введение
Начертательная геометрия входит в состав учебной дисциплины федерального значения, название которой в зависимости от специальности: «Начертательная геометрия и инженерная графика», «Инженерная и машинная графика» или просто «Инженерная графика». Инженерная графика – это единственная дисциплина целью, которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей явлений и процессов.
Тема 1. Проецирование точки
Метод Монжа
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей

Рисунок 1.1 Точка в системе трех плоскостей проекций
Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y и z (абсцисса, ордината и аппликата).
|
|
|
К началу страницы
Тема 2. Проецирование прямой
Для определения положения прямой в пространстве существуют следующие методы: 1.Двумя точками (А и В). Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].
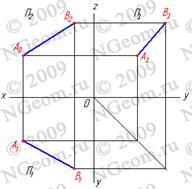
Рисунок 2.1 Определение положения прямой по двум точкам
2. Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.
|
|
|
К началу страницы
Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).

Рисунок 3.1 Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).

Рисунок 3.2 Горизонтальная прямая
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными илифронталями(рис.3.3).

Рисунок 3.3 Фронтальная прямая
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).

Рисунок 3.4 Профильная прямая
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально-проецирующая прямая - АВ (рис. 3.5).

Рисунок 3.5 Фронтально-проецирующая прямая
3.2. Профильно проецирующая прямая - АВ (рис.3.6).

Рисунок 3.6 Профильно-проецирующая прямая
3.3. Горизонтально-проецирующая прямая - АВ (рис.3.7).

Рисунок 3.7 Горизонтально-проецирующая прямая
К началу страницы
Тема 4. Плоскость. Способы задания плоскостей
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Способы графического задания плоскостей Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).

Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой
|
|
|
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).

Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии
3. Двумя пересекающимися прямыми (рис.4.3).

Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями
4. Двумя параллельными прямыми (рис.4.4).

Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями
Тема 5. Положение плоскости. Следы плоскости
К началу страницы
Различное положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный S1; - фронтальный S2; - профильный S3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.1).
2. Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (S^П1), называется горизонтально-проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.2).
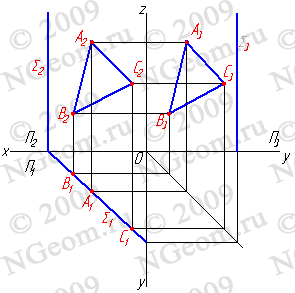
Рисунок 5.2 Горизонтально-проецирующая плоскость
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (S^П2) - фронтально-проецирующая плоскость. Фронтальной проекцией плоскости S является прямая линия, совпадающая со следом S2 (рис.5.3).
|
|
|

Рисунок 5.3 Фронтально-проецирующая плоскость
2.3. Плоскость, перпендикулярная профильной плоскости (S^П3) - профильно-проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.4).

Рисунок 5.4 Профильно-проецирующая плоскость
3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:
3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (S//П1) - (S^П2, S^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости S2 и S3 (рис.5.5).

Рисунок 5.5 Горизонтальная плоскость
3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (S//П2), (S^П1, S^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости S1 и S3 (рис.5.6).

Рисунок 5.6 Фронтальная плоскость
3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (S//П3), (S^П1, S^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости S1 и S2 (рис.5.7).

Рисунок 5.7 Профильная плоскость
Следы плоскости
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой(как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S. Горизонтальный следS1 – прямая, проходящая через горизонтальный след прямой АВ и Sx. Профильный следS3 – прямая соединяющая точки (Sy и Sz) пересечения горизонтального и фронтального следов с осями.

Рисунок 5.8 Построение следов плоскости
К началу страницы
Тема 6. Взаимное положение прямой и плоскости, точки и плоскости
Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).
|
|
|

Рисунок 6.1 Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.
Прямая линия, принадлежащая плоскости
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).
Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

Рисунок 6.2 Прямая и плоскость имеют две общие точки
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).
Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.

Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости
Главные линии в плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).

Рисунок 6.4 Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).

Рисунок 6.5 Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Рисунок 6.7 Линия наибольшего ската
|
|
|


