 |
Корпускулярно-волновой дуализм
|
|
|
|
Возможно, вы заметили в квантовой концепции света кое-что странное. Говорить, что свет существует в виде квантов, фотонов, — значит утверждать, что свет состоит из частиц, подобных песчинкам. Однако такое утверждение во многом противоречит повседневному опыту, который мы получаем, имея дело со светом.
Представьте себе, например, что вы смотрите на отдаленный уличный фонарь через ткань матерчатого зонтика. Вы не увидите непрерывный поток света, проходящий насквозь, как следовало бы ожидать, если бы свет состоял из крохотных частиц (насыпьте песка в решето, и вы увидите, что я имею в виду). Вместо этого вы увидите узор из чередующихся темных и светлых каемок, который технически называется интерференционной картиной. Свет изгибается в нитях ткани и вокруг них, создавая картину, которую могут образовывать только волны. Таким образом, даже наш повседневный опыт показывает, что свет ведет себя как волна.
Тем не менее квантовая теория настаивает, что свет также ведет себя как пучок частиц, или фотонов. Наши глаза представляют собой такой замечательный инструмент, что мы можем сами наблюдать квантовую, зернистую природу света. В следующий раз, расставаясь с близким человеком в сумерках, обратите внимание на то, как вы видите удаляющуюся фигуру. Заметьте, что очертания удаляющегося объекта выглядят фрагментарными. Если бы световая энергия, отражающаяся от этого объекта и попадающая в оптические рецепторы вашей сетчатки, обладала волноподобной непрерывностью, то как минимум какой-то свет от каждой части объекта должен был бы всегда возбуждать ваши оптические рецепторы. Вы бы всегда видели полный образ. (Следует признать, что в слабом свете контраст между темным и светлым был бы не очень ясным, но это не влияло бы на четкость очертаний.) Однако вместо этого вы видите вовсе не четкие очертания, так как рецепторы ваших глаз реагируют на индивидуальные фотоны. В тусклом свете меньше фотонов, чем в ярком; поэтому в этой гипотетической сумеречной ситуации в любое данное время будут стимулироваться лишь немногие из ваших рецепторов — слишком немногие, чтобы определять очертания слабо освещенной фигуры. Следовательно, образ, который вы видите, будет фрагментарным.
|
|
|
Возможно, вам не дает покоя еще один вопрос: почему рецепторы не могут хранить данные бесконечно, пока мозг не соберет достаточно информации, чтобы собрать все фрагментарные картины в одно целое? К счастью для квантовых физиков, которые всегда отчаянно нуждаются в повседневных примерах квантовых явлений, оптические рецепторы могут хранить информацию лишь доли секунды. В тусклом свете в любой данный момент в ваших глазах будет возбуждаться недостаточно рецепторов для создания полного изображения. Когда в следующий раз в сумерках вы будете говорить «прощай» неясной удаляющейся фигуре любимого человека, не забудьте подумать о квантовой природе света; это, несомненно, уменьшит боль вашей разлуки[8].
Когда свет рассматривается как волна, он оказывается способным одновременно быть в двух (или более местах) — как в случае, когда он проходит через отверстия ткани зонтика, и образует дифракционную картину; однако, когда мы улавливаем его на фотографической пленке, он проявляется дискретно, отдельными пятнышками, подобно потоку частиц. Таким образом, свет должен быть и волной, и частицей. Парадоксально, не так ли? Дело касается одного из бастионов старой физики: однозначного описания на естественном языке. Кроме того, на карту поставлена сама идея объективности: зависит ли природа света — то, чем является свет, — от того, как мы его наблюдаем?
|
|
|
И как если бы парадоксы, касающиеся света, были недостаточно вызывающими, неизбежно возникает еще один вопрос: может ли материальный объект, например электрон, быть и волной, и частицей? Может ли он обладать двойственностью, подобной двойственности света? Физиком, который впервые поставил этот вопрос и упорно давал на него положительный ответ, потрясший всех его коллег, был французский аристократ Луи Виктор де Бройль.
Волны материи
Когда де Бройль примерно в 1924 г. писал свою кандидатскую диссертацию, он провел параллель между дискретностью стационарных орбит атома Бора и дискретностью звуковых волн, производимых гитарой. Параллель оказалась плодотворной.
Представьте себе движение звуковой волны в некоторой среде (рис. 4). Вертикальное смещение частиц среды меняется от ноля до максимума (гребень), обратно до ноля, до отрицательного максимума (впадины), опять до ноля, и так далее с увеличением расстояния. Максимальное вертикальное смещение в одном направлении (от ноля до гребня или впадины) называется амплитудой. Отдельные частицы среды движутся взад и вперед относительно своего покоящегося положения. Однако волна, проходящая через среду, распространяется. Волна представляет собой распространяющееся возмущение. Число гребней, проходящих через данную точку за секунду, называется частотой волны, а расстояние от гребня до гребня — длиной волны.
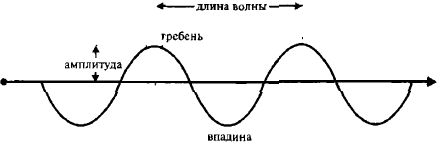
Рис. 4. Графическое представление волны
Щипок гитарной струны приводит ее в движение, но возникающие колебания называются стационарными (стоячими волнами), поскольку они не распространяются за пределы струны. В любом данном месте струны смещение частиц струны меняется во времени: имеет место волнистость, но волны не распространяются в пространстве (рис. 5). Распространяющиеся волны, которые мы слышим, приводятся в движение стоячими волнами колеблющихся струн.

Рис. 5. Первые несколько гармоник стационарной, или стоячей, волны в гитарной струне
Музыкальная нота гитары состоит из целого ряда звуков — спектра частот. Де Бройля заинтересовало то, что стоячие волны гитарной струны создают дискретный спектр частот, называемых гармониками. Звук самой низкой частоты называется первой гармоникой, которая определяет слышимый нами тон. Более высокие гармоники — музыкальные звуки, придающие ноте ее характерное качество, — имеют частоты, кратные частоте первой гармоники.
|
|
|
Стационарность представляет собой свойство волн в ограниченном пространстве. Такие волны легко вызвать в чашке чая. Де Бройль спрашивал — являются ли электроны атома локализованными (удерживаемыми) волнами? Если да, то образуют ли они дискретные стационарные волновые паттерны? Например, может быть, самая низкая атомная орбита — это та, на которой один электрон образует стационарную волну наименьшей частоты — первую гармонику, — а более высокие орбиты соответствуют стационарным электронным волнам более высоких гармоник (рис. 6).

Рис. 6. Идея де Бройля: не могут ли электроны быть стационарными волнами в ограниченном пространстве атома?
Разумеется, де Бройль приводил в поддержку своей идеи гораздо более сложные доводы, но все равно ему было трудно добиться одобрения своей диссертации. В конце концов ее послали на отзыв Эйнштейну. Эйнштейну, который первым осознал двойственную природу света, было не трудно понять, что де Бройль вполне мог быть прав: материя вполне может быть такой же двойственной, как свет. Де Бройлю присудили искомую степень, когда Эйнштейн дал о его диссертации такой отзыв: «Это может выглядеть безумным, но, в действительности, это логично».
В науке окончательным арбитром всегда служит эксперимент. Правильность идеи де Бройля о волновой природе электрона блестяще продемонстрировал эксперимент, в котором пучок электронов пропускали через кристалл (трехмерный «зонтик», подходящий для дифракции электронов) и фотографировали. Получилась дифракционная картина (рис. 7).

Рис. 7. Концентрические дифракционные кольца показывают волновую природу электронов
Если материя — волна, язвительно заметил один физик другому в конце проходившего в 1926 г. семинара, посвященного волнам де Бройля, то должно быть волновое уравнение, описывающее волну материи. Физик, которому принадлежало это замечание, сразу же забыл о нем, но тот, кто его услышал, — Эрвин Шрёдингер — в дальнейшем открыл волновое уравнение для материи, теперь известное как уравнение Шредингера. Оно является краеугольным камнем, заменившим в новой физике законы Ньютона. Уравнение Шрёдингера используется для предсказания всех удивительных качеств субмикроскопических объектов, обнаруживаемых в наших лабораторных экспериментах. Вернер Гейзенберг открыл это же самое уравнение еще раньше, но в менее четкой математической форме. Математический формализм, выросший из работ Шрёдингера и Гейзенберга, называется квантовой механикой.
|
|
|
Предложенная де Бройлем и Шрёдингером идея волны материи порождает удивительную картину атома. Она объясняет простыми терминами три самых важных свойства атомов: их устойчивость, их тождественность друг другу и их способность восстанавливаться. Я уже объяснял, как возникает устойчивость, — это был великий вклад Бора. Тождественность атомов определенного вида — это просто следствие тождественности волновых паттернов в ограниченном пространстве; структура стационарных паттернов определяется тем, каким образом ограничивается движение электронов, а не их окружением. Музыка атома, его волновой паттерн, остается одной и той же, независимо от того, где он находится — на Земле или в туманности Андромеды. Более того, стационарный паттерн, зависящий только от условий своего ограничения, не имеет никаких следов прошлой истории, никакой памяти; он снова и снова восстанавливается в том же самом виде.
Волны вероятности
Волны электронов не похожи на обычные волны. Даже в эксперименте по дифракции индивидуальные электроны обнаруживаются на фотографической пластинке как локализованные индивидуальные события; только наблюдая паттерн, создаваемый всем пучком электронов, мы обнаруживаем свидетельство их волновой природы — дифракционную картину. Волны электронов — это волны вероятности, говорил физик Макс Борн. Они дают нам вероятности: например, мы, весьма вероятно, обнаружим частицу там, где волновые возмущения (или амплитуды) велики. Если вероятность нахождения частицы мала, амплитуда волны будет слабой. Представьте себе, что вы наблюдаете уличное движение с вертолета, висящего над улицами Лос-Анджелеса. Если бы автомобили описывались уравнением Шрёдингера, мы бы сказали, что волна сильна в местах транспортных пробок, а между пробками волна слаба.
Кроме того, волны электронов принято представлять как волновые пакеты. Используя понятие пакетов, мы можем делать амплитуду волны большей в определенных областях пространства, и малой во всех остальных местах (рис. 8). Это важно, поскольку волна должна представлять локализованную частицу. Волновой пакет — это пакет вероятности, и Борн утверждал, что для волн электронов квадрат амплитуды волны — технически называемый волновой функцией — в некоторой точке пространства дает нам вероятность обнаружения электрона в этой точке. Эта вероятность может быть представлена колоколообразной кривой (рис. 9).
|
|
|

Рис. 8. Наложение многих простых волн образует типичный локальный волновой пакет (Из книги П. У. Аткинса «Кванты: справочник понятий», Оксфорд: Клейрдон Пресс, 1974)

Рис. 9. Типичное распределение вероятности
|
|
|


