 |
Практическая работа №1 «производная и её применение»
|
|
|
|
Алгебра и начала математического анализа; геометрия
Методические указания
По выполнению практических работ
Для студентов 2 курса заочного отделения
(4 семестр)
Заречный 2016
 |
Голянова О.Н.
Математика: алгебра и начала математического анализа; геометрия. Методические указания по выполнению практических работ для студентов 2 курса заочного отделения. 2016. – стр.24
Методические указания содержат варианты заданий для практических работ по дисциплине «Математика: алгебра и начала математического анализа; геометрия», необходимые теоретические сведения, примеры решения типовых задач. Методические указания предназначены для студентов 2 курса заочной формы обучения по специальности 38.02.04 «Коммерция по отраслям» и составлена в соответствии с рабочей программой дисциплины.
Методические указания рассмотрены на заседании цикловой методической комиссии общеобразовательных, естественнонаучных и ОГСЭ дисциплин Зареченского технологического института – филиала Пензенского государственного технологического университета.
Протокол №1 от 31.08.2016 г.
Методические указания одобрены и рекомендованы методическим советом Зареченского технологического института – филиала Пензенского государственного технологического университета для использования в учебном процессе.
Протокол №1 от 31.08.2016 г.
Содержание
Методические указания по выполнению практических работ. 4
Практическая работа №1 «Производная и её применение». 5
Практическая работа №2 «Интеграл и его применение». 15
Методические указания по выполнению практических работ
|
|
|
Практические задания являются неотъемлемой составной частью учебного процесса. Цель заданий — закрепить полученные знания по учебной дисциплине «Математика: алгебра и начала математического анализа, геометрия».
Задания для индивидуальной работы выполняются студентами в письменном виде в тетради. Для выполнения задания необходимо изучить соответствующий теоретический материал.
Студенты выполняю практическую работу №1 «Производная функции и ее применение» и Практическую работу №2 «Интеграл и его применение». Некоторые задания имеют образец решения. После проверки работы преподавателем студент, внеся исправления и дополнения в соответствии с замечаниями, предъявляет ее во время экзаменационной сессии. Выполненные практические работы являются условием допуска студента к экзамену.
Номер варианта практической работы определяется по таблице в зависимости от первой буквы фамилии.
Выбор варианта
| Первая буква фамилии | Номер варианта практической работы | Первая буква фамилии | Номер варианта практической работы | |
| А, Л, Х | Е, Р, Э | |||
| Б, М, Ц | Ж, С, Ю | |||
| В, Н, Ч | З, Т, Я | |||
| Г, О, Ш | И, У | |||
| Д, П, Щ | К, Ф |
ПРАКТИЧЕСКАЯ РАБОТА №1 «Производная и ЕЁ ПРИМЕНЕНИЕ»
Задание 1. Найти производную заданной функции
| Вариант | А | Б | В | Г |

| 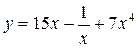
| 
| 
| |

| 
| 
| 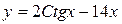
| |

| 
| 
| 
| |

| 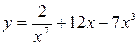
| 
| 
| |

| 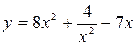
| 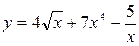
| 
| |

| 
| 
| 
| |
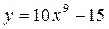
| 
| 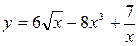
| 
| |

| 
| 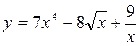
| 
| |

| 
| 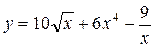
| 
| |

| 
| 
| 
|
Алгоритм решения:
Используем следующие правила и формулы нахождения производной функции
1.  , С - константа
2. , С - константа
2.  3.
3.  , С – константа
4. , С – константа
4.  5.
5. 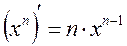
| 6.  7.
7.  8.
8. 
|
9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14. 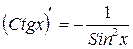
| 15.  16.
16. 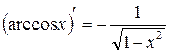 17.
17.  18.
18. 
|
Образец решения
а) 

б) 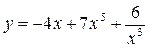

Задание 2. Вычислить значение производной в заданной точке х0
| Вариант | А | Б |
 х0 = 4 х0 = 4
|  х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
|  х0 = 1 х0 = 1
| |
 х0 = 4 х0 = 4
|  х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
|  х0 = 1 х0 = 1
| |
 х0 = 4 х0 = 4
|  х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
|  х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
|  х0 = 1 х0 = 1
| |
 х0 = 4 х0 = 4
|  х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
|  х0 = 1 х0 = 1
| |
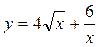 х0 = 4 х0 = 4
|  х0 = 1 х0 = 1
|
Алгоритм решения:
|
|
|
Пользуясь правилами и формулами, находим производную заданной функции.
В найденную производную подставляем заданное значение х0.
Образец решения:
 х0 = 1
х0 = 1


Ответ: 
Задание 3. Найти производную заданной функции, пользуясь правилом нахождения производной произведения
| Вариант | А | Б | В | Г |

| 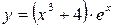
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 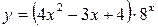
| 
| |

| 
| 
| 
| |

| 
| 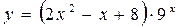
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 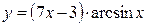
| |
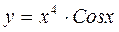
| 
| 
| 
|
Алгоритм решения:
Правило нахождения производной произведения имеет вид

Образец решения:
1) 

2) 

Задание 4. Найти производную заданной функции, пользуясь правилом производной частного
| Вариант | А | Б | В | Г |

| 
| 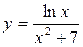
| 
| |

| 
| 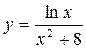
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 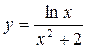
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 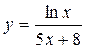
| 
|
Алгоритм решения:
Правило нахождения производной частного имеет вид 
Образец решения:
1) 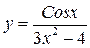

2) 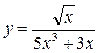
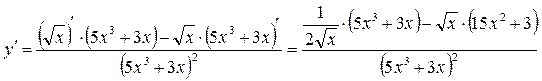
Задание 5. Составить уравнение касательной к графику функции у=f(х) в точке х0.
| Вариант | |
 х0 = 2 х0 = 2
| |
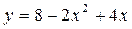 х0 = 1 х0 = 1
| |
 х0 = 2 х0 = 2
| |
 х0 = 2 х0 = 2
| |
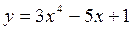 х0 = 1 х0 = 1
| |
 х0 = 1 х0 = 1
| |
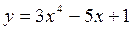 х0 = 2 х0 = 2
| |
 х0 = 1 х0 = 1
| |
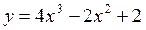 х0 = 2 х0 = 2
| |
 х0 = 2 х0 = 2
|
Алгоритм решения:
Уравнение касательной к графику функции  в точке х0 имеет вид:
в точке х0 имеет вид:

Для того чтобы составить уравнение касательно нужно:
1. Найти значение функции в точке х0, т.е. найти 
2. Найти производную заданной функции
3. Найти значение производной в заданной точке х0, т.е. найти 
4. Подставить найденные значения в уравнение касательной и упростить полученное уравнение
Образец решения:
 х0 = 1
х0 = 1
1. Находим значение функции в точке х0=1

2. Находим производную заданной функции

3. Находим значение производной в заданной точке х0=1

4. Подставляем найденные значения в уравнение касательной


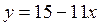
Ответ: уравнение касательной имеет вид 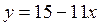
Задание 6. Материальная точка движется по закону S(t) (t – время в секундах, S – расстояние в метрах). Найти скорость движения точки и ускорение в момент времени t, если:
| Вариант | Вариант | ||
 t0 = 1 с t0 = 1 с
|  t0 = 1 с t0 = 1 с
| ||
 t0 = 1 с t0 = 1 с
|  t0 = 2 с t0 = 2 с
| ||
 t0 = 1 с t0 = 1 с
|  t0 = 1 с t0 = 1 с
| ||
 t0 = 1 с t0 = 1 с
|  t0 = 1 с t0 = 1 с
| ||
 t0 = 1 с t0 = 1 с
| 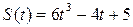 t0 = 1 с t0 = 1 с
|
Алгоритм решения:
|
|
|
Если точка движется по закону S = S(t) (t – время в секундах, S – расстояние в метрах), то скорость движения точки равна производной заданной функции  , а ускорение в момент времени t равно производной скорости
, а ускорение в момент времени t равно производной скорости 
Образец решения:
 t0 = 2 с
t0 = 2 с
Скорость движения точки в момент времени t равна

В момент времениt0 = 2 с скорость движения равна
 м/с
м/с
Ускорение точки в момент времени t равно

В момент времени t0=2 с ускорение точки равно
 м/с2
м/с2
Ответ: V = 44 м/с, а = 45 м/с2
Задание 7. Исследовать функцию на возрастание, убывание и найти экстремумы функции
| Вариант | А | Б |

| 
| |

| 
| |

| 
| |

| 
| |
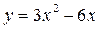
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
|
Алгоритм решения:
Алгоритм исследования непрерывной функции  на монотонность и экстремумы:
на монотонность и экстремумы:
1. Найти производную  .
.
2. Найти стационарные и критические точки. Для этого нужно приравнять найденную производную к нулю.
3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. Сделать выводы о монотонности функции:
- если на промежутке Х производная  , то функция возрастает на этом промежутке;
, то функция возрастает на этом промежутке;
- если на промежутке Х производная  , то функция убывает на этом промежутке
, то функция убывает на этом промежутке
5. Сделать выводы о точках экстремума:
- если при переходе через точку х0 производная  меняет знак с «+» на «–», то точка х0 – точка максимума;
меняет знак с «+» на «–», то точка х0 – точка максимума;
- если при переходе через точку х0 производная  меняет знак с «–» на «+», то точка х0 – точка минимума.
меняет знак с «–» на «+», то точка х0 – точка минимума.
Образец решения:

1. Находим производную  .
.
2. Приравниваем производную к нулю и решаем полученное уравнение.
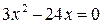 , отсюда
, отсюда 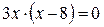
х1 = 0 х2 = 8
3.
|
 |
4. Функция возрастает на промежутках  , убывает в промежутке (0; 8).
, убывает в промежутке (0; 8).
5. Точка х1 = 0 – точка максимума, уmax = у(0) = 03 – 12∙02 + 10 = 10
Точка х2 = 8 – точка минимума, уmin = у(8) = 83 – 12∙82 + 10 = -246
Задание 8. Найти наибольшее и наименьшее значение заданной функции на заданном отрезке
| Вариант | А | Б |
 на отрезке [-1; 5] на отрезке [-1; 5]
|  на отрезке [-1; 3] на отрезке [-1; 3]
| |
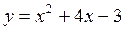 на отрезке [-4; 2] на отрезке [-4; 2]
|  на отрезке [-6; 0] на отрезке [-6; 0]
| |
 на отрезке [0; 4] на отрезке [0; 4]
|  на отрезке [3; 6] на отрезке [3; 6]
| |
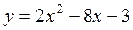 на отрезке [-1; 3] на отрезке [-1; 3]
|  на отрезке [1; 5] на отрезке [1; 5]
| |
 на отрезке [1; 7] на отрезке [1; 7]
| 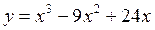 на отрезке [-2; 3] на отрезке [-2; 3]
| |
 на отрезке [-2; 5] на отрезке [-2; 5]
|  на отрезке [-6; 0] на отрезке [-6; 0]
| |
 на отрезке [-1; 5] на отрезке [-1; 5]
|  на отрезке [3; 5] на отрезке [3; 5]
| |
 на отрезке [-5; 1] на отрезке [-5; 1]
|  на отрезке [0; 4] на отрезке [0; 4]
| |
 на отрезке [-4; 1] на отрезке [-4; 1]
|  на отрезке [0; 3] на отрезке [0; 3]
| |
 на отрезке [0; 6] на отрезке [0; 6]
|  на отрезке [-6; -3] на отрезке [-6; -3]
|
Образец решения
|
|
|
Найти наибольшее и наименьшее значение функции  на отрезке [0; 2]
на отрезке [0; 2]
1. Находим стационарные точки, принадлежащие заданному отрезку. Для этого находим производную заданной функции и приравниваем её к нулю.







Из найденных стационарных точек только точка х2 = 1 принадлежит заданному промежутку
2. Находим значения производной в найденной стационарной точке
у(1) = 13 – 9∙12 + 15∙1 – 3 = 1 – 9 + 15 – 3 = 4
3. Находим значения функции на концах заданного промежутка
у(0) = 03 – 9∙02 + 15∙0 – 3 = -3
у(2) = 23 – 9∙22 + 15∙2 – 3 = 8 – 36 + 30 – 3 = -1
4. Из найденных значений выбираем наибольшее и наименьшее
уmax = у(1) = 4 уmin = у(0) = -3
Ответ: уmax = 4 уmin = -3
Задание 9. Прямоугольный лист жести имеет длину А см и ширину В см. Из этого листа требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была максимальной.
| Вариант | А | В | Вариант | А | В |
 Образец решения:
Образец решения:
Прямоугольный лист жести имеет длину
А=64 см и ширину В=40 см.
Пусть х – сторона вырезаемого квадрата.
Тогда длина коробки будет равна (64 – 2х)
ширина коробки равна (40 – 2х)
высота коробки равна х.
Вместимость коробки (т.е. объем) равна произведению длины, ширины и высоты коробки

Найдем наибольшее значение функции  на отрезке [0; 20], так как х>0 и 40 – 2х >0.
на отрезке [0; 20], так как х>0 и 40 – 2х >0.
Находим производную функции и приравниваем её к нулю.



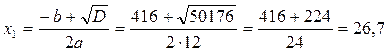



Из найденных стационарных точек только точка х2 = 8 принадлежит промежутку [0; 20].
 |
В точке х =8 функция имеет максимальное значение. Значит, сторона вырезаемого квадрата равна 8 см. Длина коробки равна 64 – 2∙8 = 48 см, ширина коробки 40 – 2∙8 = 24 см.
При этом вместимость коробки будет иметь максимальное значение
уmax = 48 ∙ 24 ∙ 8 = 9216 см3.
Ответ: сторона квадрата равна 8 см.
|
|
|


