Достоверность научных положений, рекомендаций и выводов

Обоснованность научных положений, рекомендаций и выводов, изложенных в работе, определяется корректным использованием современных математических методов, согласованным сравнительным анализом аналитических и экспериментальных зависимостей. Достоверность положений и выводов диссертации подтверждена положительными результатами внедрения разработок в ряде крупных организаций.

Практическая ценность и реализация результатов работы

Научные результаты, полученные в диссертации, доведены до практического использования. Проведены экспериментальные исследования модели с целью выдачи рекомендаций по организации работы цеха обжига цементного клинкера. Разработанные методы и алгоритмы прошли апробацию и внедрены для практического применения в ГУП «Таджикцемент» (Республика Таджикистан), а также используются в учебном процессе на кафедре "АСУ" Московского автомобильно-дорожного государственного технического университета (МАДИ). Результаты внедрения и эксплуатации подтвердили работоспособность и эффективность разработанных методов.

Апробация работы

Содержание разделов диссертации докладывалось и получило одобрение:

· на  научно-технических конференциях, симпозиумах и семинарах Республики Таджикистан (г. Душанбе,  2010-2011 гг.);

· на научно-методических конференциях МАДИ (Москва, 2008-2011 гг.),

· на заседании кафедры «Автоматизированные системы управления» МАДИ.

Содержание работы

Во введение показано актуальность, сформулированы цель и задачи исследования.

В первой главе диссертации рассмотрены технологии производства цемента. Цементная промышленность — одна из наиболее крупных и ответственных отраслей строительного производства. Сырьем для производства цементов служит смесь из извест­ковых (карбонат­ных) и глинистых пород, с соответствующими до­бавками (ГОСТ 10178-85). Цементы вы­пускают­ся на основе клин­ке­ра, по­лучаемого в результате обжига сырье­вой сме­си, вследст­вие чего в клин­кере формируются силикаты кальция (70-80%), алюминатная и алюмоферритная фазы (20-30%).

Технология изготовления цемента складывается из следую­щих операций:

Ø добыча сырья (разработка карьера);

Ø приготовление сырьевой смеси — «сырьевой передел»;

Ø спекание клинкера (обжиг);

Ø помол цементной шихты.

В зависимости от использования воды различаются сухой, мокрый и комбинированный (полусухой) способы производства.

Сухой способ целесообразен при сравнительно малой влажности и однородном составе сырья, он же практикуется в случаях, если в сырьевую смесь вместо глины вводится гранули­рованный доменный шлак. Расход топлива при сухом способе существенно меньше, чем при мокром способе.

При значительных колебаниях химического состава известня­кового и глинистого компонента чаще применяется мокрый способ, так как однородную (гомогенизирован­ную) сырьевую смесь получить легче, когда сырьевые материалы имеют высокую влажность, более мяг­кую структуру и легко диспергируются водой. Выбор мокрого спосо­ба предопределяется также в случае наличия в глине избытка посторонних примесей, для удаления кото­рых необходимо «отмучи­вание» в присутствии воды. Кроме того, при мокром способе отжига облегчается размол сырья и требуется мень­ше энергии на его измель­чение.

Мокрый способ производства используется при изготовлении це­мента из мела (карбонатный компонент), глины (силикатный ком­по­нент) и железосодержащих добавок (конверторный шлам, желе­зис­тый продукт, пиритные огарки). Способ назван мокрым из-за того, что измельчение смеси производится в водной среде, на выходе получается шихта в виде водной суспензии — «шлама» влажностью 30 – 50%. Далее шлам поступает в печь для обжига, диаметр которой достигает 4 м, а длина 150 и более метров, см. рис.1.

 

Обозначения: 1 - дымовая труба; 2 - дымосос; 3 - электрофильтр; 4 - система пылевозврата; 5 - шламовая труба; 6 - пылеулавливающая камера; 7 - цепная завеса; 8 - вращающаяся печь; 9 - головка печи; 10 - топливная форсунка; 11 - рекуператорный холодильник; 12 - решетка горячей камеры; 13 – естественный воздух; 14 - клинкерный транспортер.

 

Шарики клинкера, которые образуются на выходе из печи, растирают в тонкий порошок (который, собственно, и представ­ляет собой цемент).

При комбинированном способе производится предварительное удаление части воды из смеси — путем фильтрации: это несколько снижает расход топлива, но усложняет процесс.

Основной составляющей оборудования для обжига клинкера является вращающаяся печь, главной частью конструкции является корпус — наклонный цилиндр. Сырьевой материал переме­щается внутри корпуса благодаря его нак­лону и вращению.

Процесс теплообмена во вращающихся печах организован по принципу противотока: движение горячих газов, обра­зующихся при сжигании топлива и оттягиваемых дымососом, проти­воположно нап­равлению движения материала.

На происходящие процессы оказывает влияние множество факторов, таких как общий объем сырья, влажность, химический состав и тонкость помола шлама (или состав и количество муки), расход и калорийность топ­лива, температура и расход вторичного воздуха, неравномерность движения материала и т. п.

Вращающаяся печь в зависимости от характера процессов, протекающих в обжигаемом материале на различных ее участках, условно может быть подразделена на ряд зон — сушки, подогрева, кальцинирования, экзотермических реакций, спекания и охлаждения (загрузка, сушка, подогрев, обжиг, охлаждение и выгрузка).

Общая задача управления вращающейся печью заключается в обеспечении оптимальных тепловых режимов по сечениям печи, регулирования углов наклона и скоростей вращения цилиндра на всех стадиях рабочего процесса.

Сущность процессов получения клинкера состоит в том, что при высокой температуре в сырьевой смеси образуются компонен­ты, обеспечивающие требуемые свойства цемента. Образо­вание клинкера во вращающихся печах завершается при температурах обжигаемого материала около 1450°С — после полного связыва­ния извести.

Главная фазовая составляющая портландцементного клинке­ра — алит — должна достигать в нем 40 – 65%, в зависимости от вида клинкера. Здесь целесообразно указать на используемые сокращенные обозначения оксидов: СаО - С; SiO₂ - S; Al₂О₃ - А; Fe₂О₃ - F; Na₂О - N; Кa₂О - К.

По составу алит близок к трехкальциевому силикату C₃S, но может также содержать ряд других соединений в виде твердых растворов.

Вторая по содержанию фазовая составляющая клинкера — белит — близка по составу к двухкальциевому силикату C2S и содержит в виде твердых растворов магний, натрий, калий и др.

Третья составляющая клинкера — промежуточное вещество — образуется из той его части, которая представляет рас­плав при высоких температурах.

Остальные фазовые составляющие клинкера — целит — (твер­дые алюмоферритные растворы), трехкальциевый алюминат С₃А, а также (в небольших количествах) стеклофаза, периклаз, свобод­ная известь, и др.

Состав клинкера принято характеризовать соотношением ме­жду основными оксидами (модулями) или содержанием мине­ралов. К модульным характеристикам состава относятся:

Ø гидравлический (основной)   m = C/S + А + F;

Ø глиноземный (или алюминатный)   р = A/F;

Ø кремнеземный (или силикатный)  n = S/A + F.

Модульные характеристики удобны тем, что совпадают для клинкера исходной сырьевой смеси, однако содержание минералов полностью они не определяют. Для преодоления этого затруднения введен коэффициент насыщения кремнезема известью КН (в литературе просто «коэффициент насыщения»):

КН = (С – 1,65А – 0,35F – 0,7SO₃)/2,8S.                        (1)

Содержание клинкерных минералов рассчитывается, исходя из предположения о достижении фазовых равновесий в системе СаО - SiO₂ -Al₂О₃ - Fe₂О₃ и строгом соблюдении количест­вен­ных соотношений в peaкциях образования клинкерных минералов, в соответствии с эмпирическими формулами:

C₃S = 4,07(C – 0,7SO₃) – 7,6S – 6,72А – 1,42F;                 (2)

C₂S = 8,6S + 5,07A + l,07F – 3,07(C – 0,7SO₃);                   (3)

C₃A = 3,04F; C₄AF = 2,65(A – 0,64F); CaSO₄ = 1,7SO₃. (4)

С использованием КН содержание белита и алита опреде­лятся по следующим формулам:

 C₃S = 3,8(ЗКН – 2)S; C₂S = 8,6(1 – КН)S.            (5)    

Таким образом, теоретически значения содержания минералов в клинкере могут быть определены по известным характеристикам сырьевой смеси. Оперативный контроль качества клинкера представляет определенные трудности, так как процедуры лабораторного анализа минералогического состава достаточно длительны и трудоемки. Кроме того, содержание минералов не определяет однозначно основное качество клинкера - его активность, фактическое значение которой может быть получено только через 28 суток, а экспрессные оценки недостаточно точны. В настоящее время для этой цели разрабатываются методы оценки качества клинкера на основании кос­венных параметров.

Во второй главе представлено формализованное описание математических моделей процесса обжига цементного клинкера.

Так как технологический процесс производства цемента представляется достаточно сложным объектом, включающим самые разнородные газо- и термодинамические, механические, физические, химические и прочие яв­ления, то для формирования модели необходим комбинированный подход с разумным упрощением средств представления (принятием обоснованных «допущений»). 

В комплекс процессов, протекающих в рабочем пространстве печи, входят следующие: движение газов; горение топлива; теплообмен в пространстве печи и вблизи поверхности обрабатываемого материала (шлама); процессы теплообмена в массе материала; химические взаимодействия.

Тепловой баланс печи как объекта управления зависит от множества показателей, таких как:

Ø мощность газовых горелок являющихся основным регули­руемым источником тепловой энергии для всего процесса;

Ø направление и скорость движения горячих газов в коор­динатах печи;

Ø потери тепловой энергии через ограждения в окружающую среду;

Ø вносимые и выходящие тепловые потоки через материал, дымовые газы и технологическое оборудование.

Очевидно, что все перечисленные процессы, так или иначе, связаны между собой и подвержены взаимному влиянию.

Кинетика процессов перемещения потоков в печи можно представить в виде схемы, рис.2. Основу процесса термической обработки (обжига) цемента составляет теплообмен между газами и сырьевым материалом. Так как длина печи существенно больше ее прочих размеров, то из-за турбулентного перемешивания газового потока его параметры приб­лизительно оди­наковы для заданного сечения печи, и с определен­ными оговор­ками объект предполагается одно­мер­ным.

 

 

 

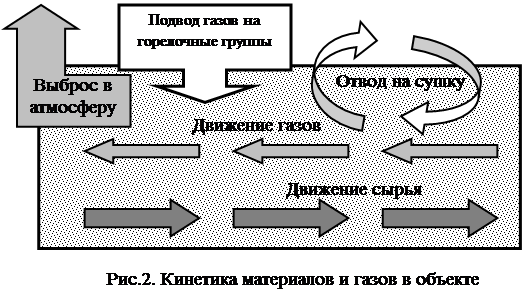
Пространство печи можно подразделить на несколько аналогичных технологических зон, условия внутри которых можно считать однородными. Время нахождения сырья в каждой из зон опреде­ляется скоростью его перемещения. Время действия газов и их свойства определяются температурой и расходом, и может различаться для разных зон.

В установившемся режиме температура газов в каждой из зон определяется условиями теплового баланса и предполагается равномерной в пределах зоны (но в общем случае может различаться в различных зонах).

Поле температуры внутри сырьевого материала в общем случае не однородно и не стационарно, поскольку тепловой обмен свя­зан с условиями молекулярной теплопроводности. Плотность тепло­вого потока через границу раздела в первую очередь зависит от разности температур газа и сырья. Количество поглощенной/выделенной при этом теплоты можно считать пропорциональным массе изменяющегося материала. При переходе в следующую зону полученные пара­метры сырья можно считать его начальной характеристикой для этой зоны.

Изменение температуры газовой составляющей для i-й зоны печи можно представить уравнением теплового баланса:

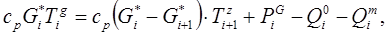  (6)

где: с_р — удельная теплоемкость газовой смеси,

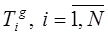— температура газовой смеси в i -й зоне.

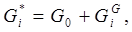                                            (7)

где: 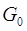 — расход воздуха в зоне горелок, 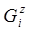— расход подаваемого воздуха, N — количество зон, 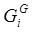— расход отбираемых дымовых газов:

                                                 (8)

 

  Q_G, — теплота сгорания газа,

    c — стехиометрическое соотно­шение газа и воздуха.

Левая часть уравнения (6) представляет поток тепла, пере­носи­мый через границу i -й и(i +1)-й зон, правая часть представ­ле­на следующими слагаемыми:

Первое слагаемое отображает поток тепла, переносимого го­рячими газами между i -й и(i +1)-й зонами.

Второе слагаемое - тепловая мощность газовых горелок в данной зоне (естественно, при отсутствии в зоне горелок = 0).

Третий член правой части — тепловые потери в окружающую среду:

                                                       (9)

где: Т₀ — температура наружного воздуха, — температура горячих газов, 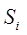— суммарная площадь ограждающей поверхности, 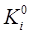— коэффициент теплопередачи.

Четвертое слагаемое в правой части — количество тепла, передаваемое материалу:

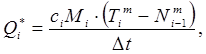                         (10)

где: 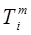- температура материала в i -й зоне, с_р - удельная теплоемкость материала, М _i - масса материала в i -й зоне, D t - время прохождения i -й зоны.

Поле температур материала определяется классическим уравнением нестационарной теплопроводности для системы без внутренних источников тепла:

   (11)

где: с _q, r _q, l _q -удельная теплоемкость, плотность, теплопроводность материала.

В качестве начальных условий можно принять температуру материала на выходе из (i – 1)-й зоны:

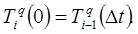.                                         (12)

Граничные условия:

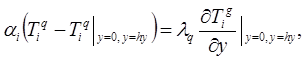         (13)

                                      Здесь hx, hy, hz — толщины прогреваемого материала в соот­ветствующих направлениях (x, y, z).                                                 В принципе уравнение (6), отражающее термодинамическую ситуацию в i -й зоне через температуру в(i +1)-й, фактически пред­ставляет собой систему из N дифференциальных уравнений. Урав­нения (6) и (11) целесообразно решать совместно методом после­довательных при­ближений, с использованием граничных условий (13) и заданных начальных условий (12).

Для моделирования объекта и формирования управляющих алгоритмов дифференциальные уравнения с граничными условиями преобразуются в систему алгебраических уравнений, соответствующих ко­нечно-разностной схеме. Блок-схема общего алгоритма представлена на рис.3.     

Во внутреннем цикле производятся расчеты изменений температуры материала по слоям, со вводом вычисленных во внешнем цикле граничных условий, и напротив, во внешнем цикле при определении текущей температуры газовой среды начальные условия используются в качестве входных величин, а вычисленные значения температуры участков определяются по вышеупомянутым зонам, распределению обрабатываемого материала, длины вращающейся печи, расположения газовых горелок и т. п.   

Явления теплопередачи через стенки печи при постоянном тепловом потоке (стационарный режим) включают теплоотдачу от газовой смеси к стенке печи, теплопроводность стенки, теплоотдачу от наружной поверхности стенки в окружающую среду. Плотность теплового потока от горячих газов внутри печного канала определится формулой:

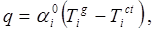                    (14)

где 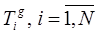 - температура газов в i –й зоне, - температура внутренней стенки, q - плотность теплового потока, 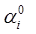- коэффи­циент теплоотдачи, N — количество зон. При стационарном режиме плотность теплового потока обусловлена теплопроводностью через печную стенку:

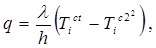    (15)

где  — температура газов в зоне, — наружная температура стенки, λ — коэффи­циент теплопроводности, h — толщина стенки.

 

Рис.3. Исходный алгоритм.

 

Тепловой поток, передаваемый в окружающую среду через наруж­ную поверхность, будет равен:

.           (16)

Сложив почленно полученные равенства, имеем:

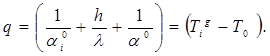       (17)

Таким образом, общий тепловой поток будет равен:

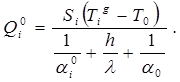               (18)

Если обозначить «коэффициент теплопередачи»:

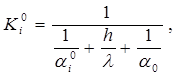                (19)

то уравнение тепловых потерь через наруж­ную поверхность примет вид:

                  (20)

В термодинамических расчетах часто используется величина «полного термического сопротивления», обратная коэффициенту теплопередачи:

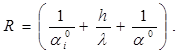               (21)

В общем случае коэффициент теплопередачи зависит от усло­вий перемешивания (характера потока, свойств составляющих, ско­рос­ти течения газо­вой смеси и т. п.).

Третья глава посвящена вопросам моделирования технологических процессов обжига клинкера при производстве цемента.

Обращаясь вновь к процессу обжига сырьевого ма­териала как объекта управления, предста­вим его как внутрен­ний элемент общей структуры, рис.4. Очевидно, что большая часть ранее перечисленных парамет­ров недоступна для регулирования. Для задачи необ­ходимо выделить параметры, доступные контролю и регулирова­нию, с тем, чтобы обоснованно отнести их к вектору управления.

В целом вектор управлений Х объединяет в себе множества функций вектора за­даний и обратной связи. В состав вектора управлений при этом входят: скорость перемещения материала; количество включенных нагревателей (горелок); параметры регулируемой мощности нагревателей; открытие заслонок на дымососе.

Заметим, что скорость перемещения материала во вращаю­щи­хся печах непосредственному управлению не подлежит: она предс­тавляется функцией свойств материала, которые также недоступны управлению и могут быть, скорее, отнесены к среде. На скорость перемещения непосредственно влияют вполне управляемые пара­метры печи — угол наклона, скорость вращения, а также свойства обрабатываемого материала (плотность, вязкость, размеры частиц), они тоже недоступны регулированию (но, тем не менее, доступны контролю).  А также влияющие на скорость, точнее — на свойства материала — его плотность, вязкость и т. п., непосредственно зависящие, во-первых, от состава материала, а во-вторых — от его температуры.

 

 

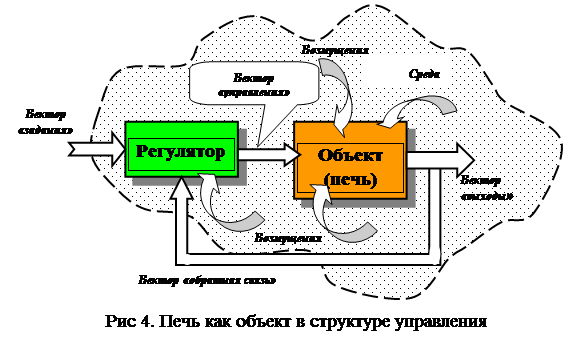В этом смысле имеем параметры управления Х:  угол наклона печи jп; скорость вращения печи wп; температура материала Тм.

Что касается последнего, температуры, то с ним тоже связа­ны определенные проблемы. Фактически он управляется не непос­ред­ственно, а путем регулирования подачи топлива в нагреватели, а также их расположением и включением. Температура материала не распределена по печи равномерно, хотя в принципе контроли­руема в любой точке (зоне) печи. Неопределенны и тепловые свой­ства обрабатываемого материала, в этом смысле их в некотором смысле можно отнести и к параметрам среды: они фактически неуправляемы и труд­но контролируемы.

К вектору управления Х добавятся параметры: количество включенных нагревателей (горелок); параметры регулирования мощности нагревателей; открытие заслонок на дымососе.

Вектор влияния среды У имеет смысл объе­ди­нить с вектором состояния объекта Н и отнести к нему: тепловые свойства обрабатываемого материала; параметры нагнетаемых газов; температуру окружающей атмосферы; параметры теплоотвода; параметры газоотвода.

Выходной вектор Z: масса (расход) полученного клинкера; характеристики клинкера; параметры отводимых газов.

Сложность объекта, неопределенность большинства пара­мет­ров и их взаимосвязей, указывают на целесообразность прибегнуть для решения задачи управления к методам имитационного моделирования.

К наиболее популярным системам имитационного моделиро­вания относятся AnyLogic, Aimsun, Arena, GPSS, ИМИТАК, Triad.Net, РДО, PTV, Tecnomatix Plant Simulation, NS-2, Transyt, Vision VISSIM, eM-Plant, Powersim.

Моделирование технологических процессов термической обработки цементного клинкера проведено в диссертации с использованием системы имитационного моде­лирования РДО (РЕСУРСЫ – ДЕЙСТВИЯ – ОПЕРАЦИИ), которая позволяет более глубоко и точно учитывать особенности динамики объекта автоматизации. В среде РДО удобно не только проводить имитационное моделирование технологического процесса, но и проводить анимацию для наблюдения его хода в реальном времени, что немаловажно при решении задач оптимизации управления.

Сложная динамическая система на концептуальном уровне пред­ставляется в виде множества некоторых взаимодействующих между собой ресурсов.

Ресурс — это элемент сложной системы, внутренней структурой которого можно пренебречь, в то время как его наличие и свойства как целого важны для целей описания.

Все ресурсы Сложных Дискретных Систем (СДС) образуют некоторое множество:

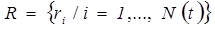                   ,  (22)

где: r_i — i- ый ресурс СДС, а N(t) — число ресурсов СДС в данный момент времени. Основным составляющим СДС, каковыми являются ее элементы, производственный процесс, законы функционирования, соответствуют следующие информационные объекты: ресурсы, действия, нерегулярные события и операции. Представление СДС в РДО-методе показано на рис.5.

 

 

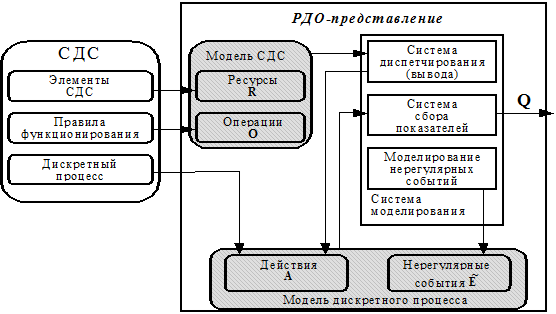
Рис.5. Представление СДС в РДО-методе

 

Ресурсы могут быть разбиты на несколько типов; каждый ре­сурс определенного типа описывается одними и теми же пара­метрами.

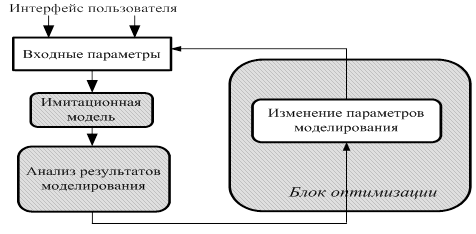
В среде РДО можно моделировать информационные потоки с различными законами распределения (равномерным, нормальным, экспоненциальным и т. п.). Обобщенно процесс анализа системы посредством вычис­лительной модели показан на рис.6.

Процесс моделирования начинается с определения структуры системы, на основе которого устанавливаются границы составляю­щих модели и необходимый уровень детализации моделируемых про­цес­сов. Обосновывается выбор зависимых и независимых пере­менных, опреде­ляется тип модели (стохастическая, детерминиро­ванная и др.). Исходные данные определяются на основе эмпири­чес­ких данных, иден­тификации и специфи­кации определяемых переменных. Что касается рассматриваемого технологического процесса — термической обработки цементного клинкера, то для формирования исходных данных необходимо учитывать сложность объекта: про­цесс обжига клинкера в печи подвержен влиянию множества раз­нородных факторов. Главные из них — количество, химический сос­тав шлама, расход, температура, калорийность топлива, расход и темпера­тура вторичного воздуха и множество других.       

  

Рис.6. Обобщенное представление процесса моделирования

 

Исходные данные и начальные условия, уровень детализации которых на начальном этапе определяется оператором, могут быть представлены, например, в виде некоторой матрицы, строки кото­рой соответст­вуют определенной операции процесса, а столбцы как раз и являются харак­теристиками операции. Успешность моделиро­вания за­висит от того, насколько хорошо оператор умеет выделять существен­ные элементы и взаимосвязи между ними.

Исходя из специфики технологического процесса, могут быть сформулированы следующие ограничения на:

־ количество операций, заданных технологией;

־ последовательность вы­полнения операций;

־ расход шлама;

־ производительность печи (по техническому паспорту печи);

־ удельный расход условного топлива;

־ влажность шлама, температура вторичного воздуха;

־ скорость вращения печи (не более 1 об/мин).

Частота поступления шлама в печь может быть определена, например, законом распределения, устанавли­ваю­щим длительность интервалов между входными сигналами предыдущей операции.

Перечисленные ограничения представляются общими для лю­бого варианта исходных данных.

В четвертой главе решаются задачи разработки имитационной модели и проведения имитационных экспериментов.

Исходным этапом моделирования представляется определе­ние ресурсов мо­дели, в данном случае — элементов вращающейся печи, которые непосредственно связаны с процессами обжига и охлаждения клин­кера. В качестве таковых выступают определенные параметра агрегата, технологические зоны печи, устройства контро­ля и управ­ления, так что для конкретной задачи могут быть предложены различные варианты моделей. Наиболее рациональным решением представ­ляется расс­мотрение печи в целом — агрегата для получения клинкера — как единого ресурса, поскольку именно в этой модели возможно размещение и хра­нение практически всей инфор­мации об его функционировании.

С целью последовательного улучшения технологического ре­жима вращающегося печи и снижения удельного расхода топлива целесообразно обеспечить следующие условия:

Ø Нормализация работы шламопитателя.

Ø Снижение удельного расхода топлива на обжиг клинкера.

Ø Увеличение часовой производительности печи.

Имитационное моделирование представляет собой процесс построения обобщенной компьютерной модели с алгоритмическим описанием основных правил ее поведения.

В методе РДО знания о моделируемой системе представляют­ся в виде модифицированных продукционных правил. Состояние любого моделируемого объекта системы определяется набором значений параметров всех элементов, принадлежащих системе и соответствующей базе данных (БД).

Пусть характеристики системы Z_i (t) будут случайными функциями времени, зависящими от параметров τ ₁, τ ₂, …, τ_n. Разобьем эти параметры на две группы: управления — τ ₁, τ ₂, …, τ_m, опреде­ляющие дальнейший порядок функционирования системы, и собственные — τ_{m +1}, τ _{m +2}, …, τ_n, характеризующие свойства системы и ее элементов и не зависящие от управления. Пусть некоторое свойство системы описывается функционалом Ф, взятым в качестве показателя и определенным в пространстве Z_i (t):

Ф = Ф(τ ₁, τ ₂, …, τ_m; τ_{m +1}, τ _{m +2}, …, τ_n).  (23)

На величины τ_i накладываются ограничения вида:

λ_i (τ ₁, τ ₂, …, τ_m; τ_{m +1}, τ _{m +2}, …, τ_n),            (24)

                h = 1, 2, …, h ^*, 0 ≤ τ_j ≤ α_i.                    (25)

Можно утверждать, что задача оптимального управления сведется к выбору параметров τ_{m +1}, τ _{m +2}, …, τ_n, удовлетворяющих условиям (24) и обеспечивающих минимум функционала Ф (23).

Если Ф = Ф(τ ₁, τ ₂, …, τ_n) и λ_h (τ ₁, τ ₂, …, τ_n), заданные модели­рующим алгоритмом, является выпуклыми и непрерывно диффе­ренцируемыми функциями n переменных, то задача выбора опти­мального управления асимптотически эквивалентна задаче нахож­дения минимума функции

                          (26)

при условиях 0 ≤ τ_j ≤ α_i (c > 0 — некоторое постоянное число). Под асимптотической эквивалентностью мы будем понимать эквивалентность при c → ∞. Таким образом, в результате замены (23) эквивалентным соотношением (26) мы пришли к задаче, которая может быть решена любым из известных методов отыскания экстремума.

Суть его сводится к следующему. Пусть искомыми величинами будут τ ₁, τ ₂,.., τ_w. Тогда в W -мерном пространстве выбираем произвольную точку α ₁, α ₂, …, α_n, которую будем называть точкой нулевого приближения, а значение V (τ ₁, τ ₂, …, τ_w) обозначим V ⁰. Отправляясь от этой точки, используем итерационную процедуру покомпонентной минимизации величины V как функции одной переменной. Минимизация функции V по каждой переменной может быть проведена различными способами. Рассмотрим алгоритм минимизации функции:

,

приняв во внимание физи­ческую особенность функционирования технологической операции:

при  и .

Пусть минимум функции находится в интервале (0, τ), то есть, правая граница интервала неизвестна. Произвольно выбираем значение аргумента τ = τ ₁ и методом агрегативного моделирования определяем функционал F ₁ при этом аргументе, соответственно увеличиваем значение аргумента          τ = τ ₂ = 2 τ ₁. Значение функцио­нала F ₂ варьируется аналогичным образом — до тех пор, пока не выполнится условие

F_n > F ₁ (n = 2, 3, 4, …).

Для определения левой границы интервала поступаем следующим образом. Интервал (0, τ) делим пополам (значение функ­ции при аргументе τ / 2 было определено при поиске правой грани­цы). Вновь полученный интервал (τ /2, τ) снова делим пополам, и в этой точке также определяем значение функции. Рассмотрим два случая взаимного соответствия этих значений.

Случай 1-й (рис.7,а). Если соблюдается условие F_A > F_B < F_N, то минимум функции находятся в интервале (a, n). Для определения минимума функции отрезки a, b и b, n делим пополам, получая, соответственно, точки c и d, и вычисляем при этих аргументах зна­чения функции (точки C, D), и далее — с заданной степенью точ­ности опреде­ляем мини­мальное значение функции методом пяти точек.    

Случай 2-й (рис.7,б). Если соблюдается условие F_A < F_B < F_N, то минимум функции находится вне пределов интервала (a, n). Для определения минимального значения отрезок 0,а делим пополам (точка С). Исключая из анализа ординату nN и определяя по методу агрегативного моделирования значение в точке С, анализируем значение функционала в точках C, A, B и, в зависимости от их вели­чин, или повторяем процедуру или поступаем таким же образом, как рассмотрено в 1-м случае.

 

 

Следует рассмотреть два метода построения моделирующего алгоритма для обеспечения требуемого согласования.

1. Для определения оптимума продолжительности работы моделируется процесс, состоящий из одной операции. В процессе моделирования регистрируются моменты выдачи выходных сигналов, их интервалы, моменты сбоя, длительность ремонта, скорость вращения печи, температура выходящего клинкера, все признаки состояний и другие представляющие интерес параметры моделируемого процесса.   

Для каждого шага моделирования регистрируются результаты промежуточных вычислений второй операции, и вновь повторяется моделирование процесса, представленного тремя, четырьмя и т. д. операциями.

 2. Аналогичным образом производится моделирование технологического процесса, состоящего из одной, двух и т. д. операций, но при этом результаты промежуточных вычислений запоминаются не по шагам моделирования ∆t, а вычисляются каждый раз для всех операций, составляющих процесс.

Ниже рассмотрен алгоритм согласования процесса моделирования по последнему методу, называемому методом ∆t. Сущность метода состоит в следующем. С помощью программ ввода и формирования в ЭВМ вводятся данные (начальные условия) о состоянии системы в момент t=0.

Вариант блок-схемы моделирующего алгоритма, приведен на рис.8.

 

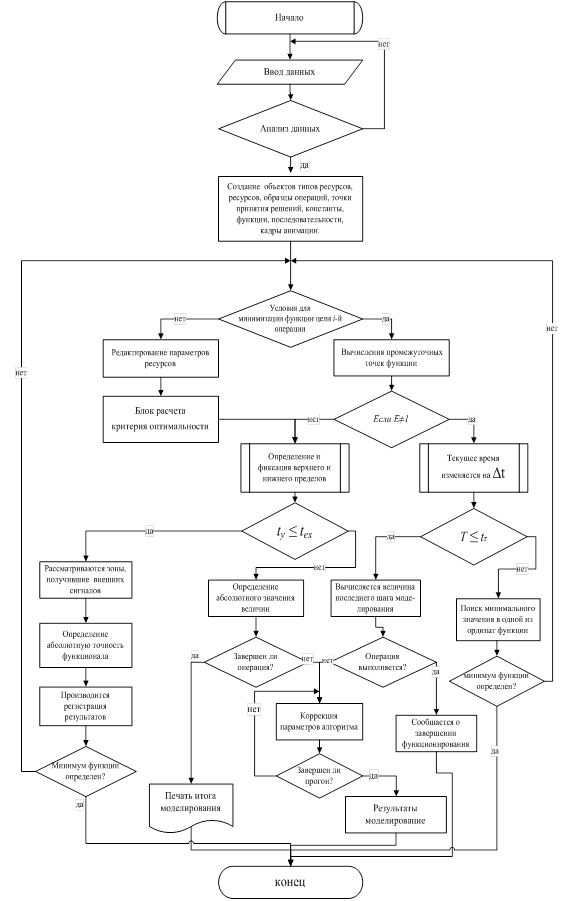
Рис.8 Схема моделирующего алгоритма

 

Затем текущее время изменяется на ∆t, то есть t₁ = ∆t и, начиная с автономного плюса, производится пересчет изменения состояний системы за интервал ∆t. Зоны, не получившие к моменту ∆t внешних сигналов, будут изменять свои состояния в соответствии с оператором U. Для них производится проверка принадлежности состояний подмножеством Z ^у и наличия в интервале ∆t моментов выдачи выходных сигналов.  

Если выходные сигналы Y соответствуют t _y ≤ t _ex (за ∆t), то рассматриваются зоны, получившие эти сигналы в качестве внешних. Моделирование продолжается до тех пор, пока состояние системы не будет зафиксировано по всем зонам. Далее текущее время снова изменяется на ∆t и процедура формирования состоя­ний и выходных сигналов повторяется.

Таким образом, для решения поставленной задачи с использо­ванием имитационной модели необходимо выделить и описать состояния системы и правила (алгоритмы) их изменения. Результаты регист­рируются в терминах выбранного средства моделирования (в частности, алго­ритмического языка), и обеспечивается их использо­вание и даль­нейшая доработка.

 

События, которые начинают или завершают действие, не планируются разработчиком модели, а инициируются по условиям, определенным по соответствующим действиям. Условия начала или окончания действий проверяются (сканируются) после очередного продвижения имитационного времени: если заданные условия удов­летворяются, то происходит соответствующее действие. Для выпол­нения каждого действия модели сканирование условий должно производиться для всего их множества при каждом шаге «имитационного» времени.

 Проведенные имитационные эксперименты показали, что смоделированная система практически полностью соответствует объекту исследования. Результаты проведенных имитационных экспериментов представлены в табл.1.

ПОКАЗАТЕЛЬ

РЕКОМЕНДУЕМЫЕ Н

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: