Главная | Обратная связь | Поможем написать вашу работу!

Метод последовательных приближений

Предположим, что (1) переписано в виде

x = f (x). (2)

Это преобразование можно сделать различными путями. Например, если

F (x) = = 0,

где с 0, то можно прибавить к правой и к левой частям х

х = (3)

или можно разделить все выражение на x и получить

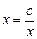. (4)

Наконец, можно преобразовать уравнение к следующему виду:

(5)

Очевидно, что значения х, являющиеся корнями этого уравнения, равны ± .

Пусть будет исходным приближенным значением корня уравнения (2). Тогда в качестве следующего приближения примем

В качестве следующего приближения возьмем

Продолжая этот процесс дальше, в качестве п- гоприближения необходимо положить

(6)

Основной вопрос, который необходимо выяснить при пользовании этим методом,— сходится ли х_п к решению уравнения (2) при возрастании ?

Мы выведем сейчас достаточные условия для сходимости метода; иными словами, выведем условия, которые являются гарантией того, что последовательные значения х_п будут приближаться к решению уравнения (2). Необходимо отметить, что эти условия не являются необходимыми, так как существуют функции, для которых эти условия не выполняются, но для которых тем не менее с помощью (6) можно найти их решения.

Рассмотрим сначала геометрическое представление процесса. При решении уравнения (2) отыскивается точка пересечения кривой и прямой . Рассмотрим рис. 1, на котором изображена некоторая кривая . Кривая эта может представлять собой какую угодно функцию, но для нас сейчас важно то обстоятельство, что производная этой кривой положительна и меньше 1, т.е. . Пусть – значение х в точке пересечения; тогда а является корнем этого уравнения. Естественно, приступая к решению задачи, мы не знаем значения корня.

Зададимся некоторым . Значение 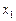равно . Так как ОА на рис. 1 равно , то найти 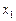можно следующим образом: проведем через точку А горизонтальную линию до пересечения с прямой в точке В, как показано на рисунке. Значение можно найти, проведя через точку В вертикальную линию до пересечения с кривой . При этом мы получаем отрезок ОС, равный , и проводя через точку С горизонтальную линию до пересечения с прямой , получаем . Процесс продолжается в том же порядке и дальше; на рисунке последовательность операций показана стрелками.

На рисунке видно, как последовательные значения х сходятся к . Важно помнить, что для рассмотрения мы взяли кривую, производная которой положительна и меньше 1.

Рис. 1. Геометрическое представление метода последовательных приближений для .

Рассмотрим теперь другую кривую , производная которой отрицательна, но меньше 1 по абсолютной величине. Этот случай изображен на рис. 2. Последовательные операции вычисления решения этого уравнения снова изображены стрелками; приближения опять сходятся к решению . В противоположность тому, что имело место для функции с положительной производной (см. рис. 1), на этот раз каждое последующее приближение находится с противоположной стороны от х = а. Для функции с положительной производной все последовательные приближения находились с одной стороны от истинного значения корня.

Наконец, рассмотрим случаи, когда производная функции больше 1 (рис. 3) и меньше –1 (рис. 4). В обоих случаях метод расходится. Каждое последующее значение х отстоит дальше от истинного значения корня, чем предшествующее. Поэтому кажется обоснованным предположение, что итерации по формуле (6) сходятся при условии,

Рис. 2. Геометрическое представление метода последовательных приближений для .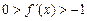

что производная меньше 1 по абсолютной величине.

Действительно, именно так и обстоит дело, и сейчас мы в этом убедимся с помощью элементарных выкладок. Заметим, что

так что

Умножая правую часть на и используя теорему о среднем значении, получаем

где лежит между и .

Рис. 3. Геометрическое представление метода последовательных приближений для .

Теперь пусть m будет максимальным значением во всем рассматриваемом интервале, т. е. в интервале, включающем в себя . Тогда

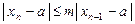Таким же образом получаем

и поэтому

Рис. 4. Геометрическое представление метода последовательных приближений для .

Продолжая те же выкладки, получаем

. (7)

Очевидно, что, если во всем интервале m <1, то независимо от выбора начального значения с возрастанием п правая часть неравенства становится малой и сходится к а.

С другой стороны, для случая величина неограниченно возрастает с ростом п. Доказательство этого мы предоставляем читателям.

Таким образом, если , то процесс сходится, если же , то процесс расходится. Обратите внимание, что неравенства должны выполняться при всех значениях х _п, вычисляемых в ходе решения задачи.

Что произойдет в случае, когда производная в некоторых точках x_i меньше, а в других точках x_j больше 1 по абсолютной величине? Точного ответа на этот вопрос не существует, процесс иногда сходится, иногда расходится.

Вернемся к примеру, рассмотренному в начале раздела, где корнями уравнения являются ± . В формуле (3)

так что , если –l< x <0. В этом случае, если число с меньше 1, то процесс сходится к отрицательному значению корня.

С другой стороны, если воспользоваться формулой (4), то

и при х, близких к (как и должно быть при отыскании корня уравнения), 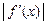становится почти равным 1; можно проверить, что процесс расходится.

Наконец, применяя формулу (5), получаем выражение для в виде

В этом случае когда , то и процесс очень быстро сходится.

Вообще говоря, хотя для всякого уравнения можно найти большое количество соответствующих ему функций f(x) в выражении (2), нужно с большой осторожностью подходить к их конкретному выбору, так как от него зависит сходимость метода итераций.

Воспользуйтесь поиском по сайту: