 |
Формализация предметной области
|
|
|
|
АНАЛИТИЧЕСКИЙ ОБЗОР ПРОБЛЕМЫ РАЗМЕЩЕНИЯ МНОГОУГОЛЬНИКОВ
Обзор литературы
Задача, рассматриваемая в работе, принадлежит к классу задач нерегулярного размещения. Их общая задача состоит в поиске такого варианта расположения объектов, при котором заданный критерий качества размещения, например метрические характеристики области, достигает оптимума, а для размещаемых объектов выполняются ограничения на взаимное размещение (условие взаимного непересечения) и ограничения на положение объекта в области размещения.
Интерес к множеству задач размещения вызван, с одной стороны, их сложностью и нетривиальностью математических моделей, необходимых для адекватного описания, а с другой стороны - широким спектром практических приложений.
Наиболее изученным является класс задач размещения прямоугольников (прямоугольных параллелепипедов) в прямоугольной области для которых разработаны эффективные эвристические методы.
Анализ работ позволяет сделать следующие выводы. Если статья посвящена описанию точной математической модели задачи размещения в терминах классического математического программирования, то отсутствует описание алгоритма и его реализации, построенных на основании математической модели. С другой стороны, если в работе говорится о численных результатах и приводятся примеры решенных задач, то методология решения основана на эвристиках и нет доказательства оптимальности полученного решения. Кроме того, математические модели, которые рассматриваются в указанных работах, не позволяют говорить даже о локальном экстремуме.
В нашей стране одной из первых фундаментальных работ, посвященных изучению методов размещения геометрических тел с учетом их формы и размеров, является монография Л.В. Канторовича и В.А. Залгаллера [1]. В ней для построения оптимальных планов раскроя плоских материалов на прямоугольные заготовки используется метод разрешающих индексов, предложенный Л.В. Канторовичем.
|
|
|
Для задач размещения объектов более сложной формы непосредственное применение указанных методов, однако, оказалось невозможным и для решения практических задач такого рода широко использовались различные эвристические приемы.
Важным шагом вперед, позволившим аналитически описывать объекты сложной геометрической формы и использовать математический аппарат классического анализа для их исследования, было создание В.Л Рвачевым теории R-функций [2]. Однако непосредственное применение R-функций при решении задач нерегулярного размещения геометрических объектов сложной формы для описания условий их взаимного непересечения оказалось излишне громоздким и требующим значительных вычислительных затрат.
Универсальный конструктивный математический аппарат, позволяющий строить аналитическое описание условий взаимного расположения объектов с учетом любых технологических ограничений, был разработан в работах научной школы, возглавляемой Ю.Г. Стояном.
Первым шагом в этом направлении было создание функции плотного размещения, её годографа, и построение на этой основе методологии последовательно-одиночного размещения [3,4]. Это позволило осуществить разработку автоматической (без участия человека) системы решения задач размещения достаточно большого набора объектов нерегулярной формы. Получаемые результаты давали хорошие приближения к локальному, а иногда и к глобальному минимуму. Большое количество экстремумов задачи вызвало необходимость перебора приближений полученных решений к локальным экстремумам.
|
|
|
В дальнейшем методология построения точной математической модели и методов решения исследуемой задачи получила должное развитие в работе Стояна Ю.Г. [5], введено понятие Ф-функции, формализующей геометрические отношения непересечения геометрических объектов и являющиеся качественной мерой выполнения этих отношений.
После появилась теория, обосновывающая построение структур линейных неравенств, для условий непересечения. Понятие структуры линейных неравенств, задающей в евклидовом пространстве некоторое точечное множество, тесно связано с предикатным описанием этого множества. Оно использует неравенства в качестве элементарных предикатов и обычные логические операции, заданные на бинарных множествах (дизъюнкции, конъюнкции и т.д.)
На сегодняшний день задача размещения объектов произвольной формы продолжает оставаться актуальной во многих отраслях промышленной деятельности. Поэтому необходимо удовлетворять условиям непересечения объектов. Для построения этих условий будем использовать Ф-функции и их предикатное представление. Неотрицательная область Ф-функции может быть описана несколькими способами:
с помощью предикатного описания [6];
с помощью R-функций [2];
с помощью структур линейных неравенств [7].
R-функции позволяют представить Ф-функции с помощью дифференцируемой функции, которая, однако, оказывается нелинейной. В работе для описания Ф-функции выбран предикатный метод описания, т.к. он первичный для R-функций и структур линейных неравенств.
Формализация предметной области
В работе дана полубесконечная полоса с фиксированной шириной, на которой необходимо оптимально разместить заданное количество ориентированных многоугольников, так чтобы они не пересекались.
Для описания полосы введем следующие обозначения:
 - полубесконечная полоса;
- полубесконечная полоса;
b - ширина полосы;
 - длина полосы.
- длина полосы.
С полосой свяжем неподвижную систему координат с началом в левом нижнем углу (рис. 1.1).

Рисунок 1.1 - Полубесконечная полоса
С каждым многоугольником, помещённым в полосу, свяжем собственную систему координат. Центры этих систем называются полюсами многоугольников. Координаты полюсов будем задавать относительно неподвижной системы координат полосы.
|
|
|
Введем обозначения (рис. 1.2):
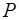 - многоугольник, размещаемый в полосе;
- многоугольник, размещаемый в полосе;
 - набор размещаемых многоугольников;
- набор размещаемых многоугольников;
 - количество вершин (сторон) i-ого многоугольника;
- количество вершин (сторон) i-ого многоугольника;
 - координаты полюса i-го многоугольника в неподвижной системе координат;
- координаты полюса i-го многоугольника в неподвижной системе координат;
 - r-я вершина i-го многоугольника, где
- r-я вершина i-го многоугольника, где  ;
;
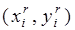 - координаты r-й вершины i-го многоугольника в собственной системе координат (СК);
- координаты r-й вершины i-го многоугольника в собственной системе координат (СК);
 - r-й отрезок границы i-го многоугольника, где
- r-й отрезок границы i-го многоугольника, где  . Здесь и далее будем полагать, что
. Здесь и далее будем полагать, что  .
.
Набор координат всех полюсов относительно неподвижной СК и будет составлять размещение в полосе.
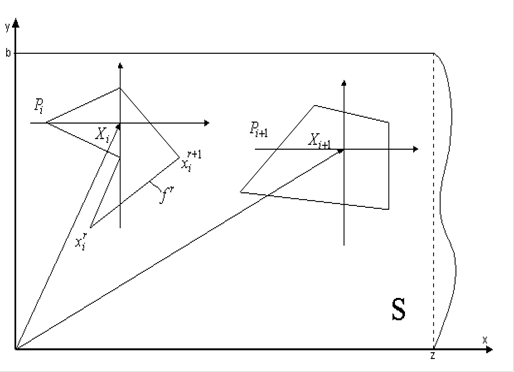
Рисунок 1.2 -
|
|
|


