Сравнительный анализ интерполяционных методов синтеза регуляторов

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Школа: Инженерная школа информационных технологий и робототехники

Направление подготовки: 15.04.06 Мехатроника и робототехника

Отделение школы (НОЦ): _ Отделение автоматизации и робототехники

 

ОТЧЕТ

Научно-исследовательской практике

 

на тему: Сравнительный анализ интерполяционных методов синтеза регуляторов

 

Выполнил: студент гр._ 8ЕМ81 ________        ___________       Кудайбергенов А.К

(Номер группы)         (Подпись)          (Ф.И.О.)

 

 

Дата сдачи  преподавателю       _____ _____________ 2019 г.

 

 

Научный руководитель  ___ доцент ОАР_______ _______         ___ Воронин А.В_

                     (Ученая степень, ученое звание, должность)             (Ф.И.О.)

 

_____________________            ________________________________

                             (Оценка руководителя)                                (Подпись)

                      

 

_____ _____________ 2019 г.

   (Дата проверки)

 

Руководитель научно-исследовательской практики_доцент       ___ Суханов А.В_

                     (Ученая степень, ученое звание, должность)             (Ф.И.О.)

 

_____________________            ________________________________

                              (Оценка руководителя)                               (Подпись)

 

Томск – 2019

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ИНТЕРПОЛЯЦИОННЫХ МЕТОДОВ СИНТЕЗА РЕГУЛЯТОРОВ

              Интерполяционные методы синтеза регуляторов построены на той же идеологии, что и обычные частотные методы. Для одномерной системы они предполагают выбор желаемой разомкнутой или замкнутой передаточной функции, а затем, параметрический синтез регулятора так, чтобы желаемая и синтезированная передаточные функции совпадали при некоторых значениях аргументов.

Пусть система управления представлена рис. 1.

 

Рис.1 Структура системы управления

 

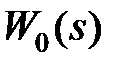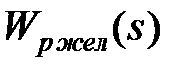Известна модель объекта управления в форме передаточной функции  и модель желаемой системы в форме передаточной функции замкнутой  или разомкнутой  системы. Поскольку связь между  и 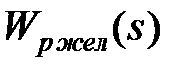, в рамках заданной структуры, однозначна, обычно используется 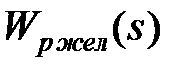, так как это приводит к более простым соотношениям.

Передаточная функция регулятора может быть вычислена по формуле

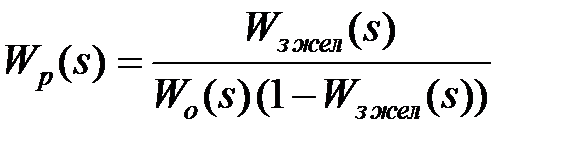,(1)

если используется , или

,                     (2)

если используется .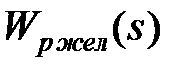

Особенность интерполяционных методов в том, что приведенные равенства (1,2) должны выполняться, в общем случае, только в некоторых заданных точках, при некоторых значениях аргумента, которые называются узлами интерполяции. Выражение (2) приобретает вид

,

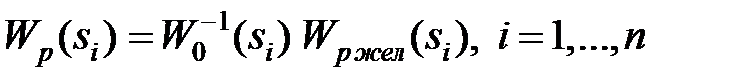где 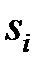 - узлы интерполирования.

Таким образом, интерполяционные подходы нацелены на достижение приближенного решении, что позволяет, в принципе, обеспечить как приемлемые динамические характеристики, так и устойчивость и грубость синтезированных систем. Они позволяют формализовать задачу синтеза и, что не менее важно, решать на единой методологической основе задачи синтеза одномерных и многомерных систем управления. Из-за своей приближенности они обычно реализуются в рамках итерационных процедур синтеза регуляторов на ЭВМ, [1].

Конкретные реализации интерполяционного метода зависят, прежде всего, от выбора узлов интерполирования. В отмечаются следующие варианты выбора узлов интерполирования

1. Расположение всех узлов на мнимой оси. Это соответствует приближению частотных характеристик желаемой и синтезируемой систем. В этом случае аргументы выражений (1), (2) принимают чисто мнимые значения комплексной частоты, а сами равенства (1), (2) представляют собой комплексные уравнения относительно коэффициентов регулятора .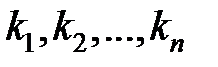

Для численных расчетов от комплексных выражений переходят в область действительных чисел, записывая каждое равенство для действительной и мнимой составляющих, т.е. для ВЧХ и МЧХ. Результатом является система линейных или нелинейных алгебраических уравнений относительно коэффициентов регулятора.

Обычно число узлов интерполирования выбирается так, чтобы полученная система имела однозначное решение. При этом число уравнений принимается равным числу неизвестных коэффициентов.

2. Расположение всех полюсов на вещественной оси (положительные вещественные числа). Данный подход позволяет использовать в качестве желаемой временную характеристику замкнутой системы [2].

Такая замена приводит к тому, что роль частотной характеристики в вещественном интерполяционном методе выполняет некоторая вещественная передаточная функция 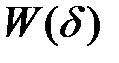, называемая численной характеристикой. Предполагается, что эта характеристика, являясь результатом интегрального преобразования, несет ту же информацию об объекте, что и обычные частотные характеристики. Однако, поскольку численная характеристика  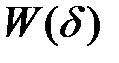функция вещественная, работать с ней при синтезе систем управления значительно проще [3].

Проведем сравнение двух указанных подходов к синтезу регуляторов на простом примере.

Передаточная функция объекта управления имеет вид:

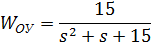
Принимаем в качестве желаемой передаточную функциювторого порядка.

Желаемая передаточная функция синтезируемой системы имеет вид:

Из (1) определим передаточную функцию желаемой замкнутой системы системы:

 

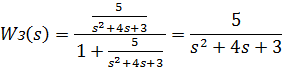
Также известно, что

,(3)                                                            (60)

где W _{P ег} (s) – передаточная функция регулятора; W_ОУ (s) – передаточная функция объекта управления.

Выбираем желаемый вид передаточной функции регулятора:

(4)

Далее для синтеза регулятора по данному методу необходимо заменить s на δ:

В уравнении (4) имеем пять неизвестных: b ₁, 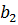b ₀ и a ₁ a ₂. Для того чтобы их определить, необходимо выбрать пять значений δ ₁, δ ₂, δ ₃, δ₄,δ₅ подставить их по очереди в уравнение (4). Таким образом, получаем систему линейных алгебраических уравнений размерности пять с пятью неизвестными.

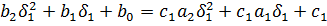
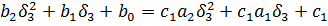
По такому же принципу находим уравнения, используя частотный интерполяционный метод:

Присвоим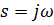

Тогда желаемый вид передаточной функции регулятора будет выглядеть следующим образом:

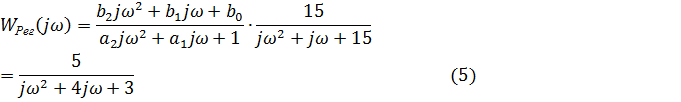
Выберем три уравненияи выделим действительную и мнимую части:

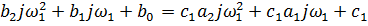
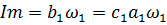
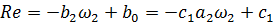
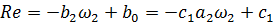
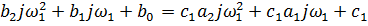
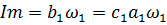
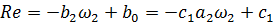
В результате сравнения двух методов синтеза регуляторов можно выдвинуть следующее:

Достоинством вещественного интерполяционного метода является возможность и простота приближенного решения задач.

Достоинством частотного подхода является достаточно прозрачная связь частотной характеристики желаемой системы с ее устойчивостью и качеством. Приближение может обеспечиваться по АЧХ и ФЧХ. Но лучше по ВЧХ и МЧХ, т.к. это приводит к линейным уравнениям.

 

 

Списокиспользованныхисточников:

1. Вещественный интерполяционный метод в задачах автоматического управления: учебное пособие /А.С Алексеев, А.А Антропов, С.В Замятин,2009,-219с.
2. Мясковский И.Г. Основы автоматизации производства
3. Никулин А.Е. Основы теории автоматического управления. – Санкт-Петербург, 2004, - 631 с.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: