 |
Пример решения задачи по теме «Корреляционно-регрессионный анализ» (к задаче №7)
|
|
|
|
Приведены данные, характеризующие реализацию продукции и производительность труда торгового предприятия:
| № предприятия | Выполнения плана реализации продукции, % Y | Производительность труда, тыс. руб. Х |
| 103,5 | 5,34 | |
| 97,6 | 5,22 | |
| 101,1 | 5,44 | |
| 84,6 | 4,42 | |
| 5,5 | ||
| 100,2 | 4,99 | |
| 90,5 | 4,55 | |
| 102,8 | 5,49 | |
| 99,3 | 5,29 | |
| 100,1 | 5,31 | |
| 5,72 | ||
| 100,8 |
Требуется:
1) построить уравнение регрессии, считая форму связи этих показателей линейной;
2) измерить тесноту корреляционной связи между производительностью труда и выполнением плана реализации;
3) проанализировать рассчитанные показатели.
Решение:
1. Уравнение регрессии имеет вид: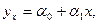 
система уравнений записывается следующим образом:
Из данной системы уравнений параметры находят по следующим формулам:
(1)
(2)
Для того чтобы построить уравнение регрессии произведем вспомогательные расчеты:
| Х | Y | XY | X2 | Y2 | Yх | |
| 5,34 | 103,5 | 552,69 | 28,5156 | 10712,25 | ||
| 5,22 | 97,6 | 509,472 | 27,2484 | 9525,76 | 99,4 | |
| 5,44 | 101,1 | 549,984 | 29,5936 | 10221,21 | 102,3 | |
| 4,42 | 84,6 | 373,932 | 19,5364 | 7157,16 | 88,6 | |
| 5,5 | 566,5 | 30,25 | 103,1 | |||
| 4,99 | 100,2 | 499,998 | 24,9001 | 10040,04 | 96,3 | |
| 4,55 | 90,5 | 411,775 | 20,7025 | 8190,25 | 90,4 | |
| 5,49 | 102,8 | 564,372 | 30,1401 | 10567,84 | ||
| 5,29 | 99,3 | 525,297 | 27,9841 | 9860,49 | 100,3 | |
| 5,31 | 100,1 | 531,531 | 28,1961 | 10020,01 | 100,6 | |
| 5,72 | 594,88 | 32,7184 | 106,1 | |||
| 100,8 | 10160,64 | 96,4 | ||||
| 62,27 | 1187,5 | 6184,431 | 324,785 | 117880,7 | 1187,5 |
Подставим итоговые значения из вспомогательной таблицы в формулы 1-2:
В нашем уравнении регрессии параметр а1 = 13,466 показывает, что с увеличением производительности труда на 1 тыс. руб. выполнение плана реализации возрастет на 13,466 %.
Таким образом, уравнение регрессии по данному примеру примет вид:
|
|
|
2. Измерим тесноту корреляционной связи между производительностью труда и выполнением плана реализации линейным коэффициентом парной корреляции:
Линейный коэффициент парной корреляции говорит о прямой связи сильной тесноты между производительностью труда и выполнением плана реализации.
Задача 2
Имеются следующие данные выборочных обследований по проблемам занятости в РФ за 2006 г. о возрастной структуре безработных:
| Возрастная группа, лет | Численность безработных, тыс. чел. |
| До 20 | 474,9 |
| 20-24 | 1079,7 |
| 25-29 | 694,8 |
| 30-34 | 464,9 |
| 35-39 | 499,9 |
| 40-44 | 499,9 |
| 45-49 | 609,8 |
| 50-54 | 419,9 |
| 55-59 | 190,0 |
| 60-72 | 65,0 |
По приведенным данным вычислите:
1) среднее значение варьирующего признака;
2) показатели вариации: размах, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации;
3) моду и медиану;
Постройте графики вариационного ряда.
Сделайте выводы.
Решение:
1) Средний возраст безработных рассчитаем по формуле средней арифметической взвешенной:
где 
– середина интервала (осредняемый признак), 
- вес признака.
Преобразуем интервальный ряд в дискретный:
Следовательно, средний возраст равен:
| Возрастная группа, лет | Численность безработных, тыс. чел.
|
| 
|
| До 20 | 474,9 | 8548,2 | |
| 20-24 | 1079,7 | 23753,4 | |
| 25-29 | 694,8 | 18759,6 | |
| 30-34 | 464,9 | 14876,8 | |
| 35-39 | 499,9 | 18496,3 | |
| 40-44 | 499,9 | 20995,8 | |
| 45-49 | 609,8 | 28660,6 | |
| 50-54 | 419,9 | 21834,8 | |
| 55-59 | |||
| 60-72 | |||
| Итого | 4998,8 | - |
Изобразим графически вариационный ряд, построим гистограмму:
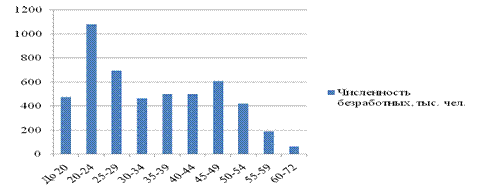
Рисунок 1 – Гистограмма распределения численности безработных в РФ за 2006 г.
2) Рассчитаем показатели вариации, построим вспомогательную расчетную таблицу:
|
| 
| 
| 
| 
| 
| 
|
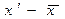
| 474,9 | -16,2 | 16,2 | 7693,38 | 262,44 | 124632,8 | |
| 1079,7 | -12,2 | 12,2 | 13172,34 | 148,84 | 160702,5 | |
| 694,8 | -7,2 | 7,2 | 5002,56 | 51,84 | 36018,43 | |
| 464,9 | -2,2 | 2,2 | 1022,78 | 4,84 | 2250,116 | |
| 499,9 | 2,8 | 2,8 | 1399,72 | 7,84 | 3919,216 | |
| 499,9 | 7,8 | 7,8 | 3899,22 | 60,84 | 30413,92 | |
| 609,8 | 12,8 | 12,8 | 7805,44 | 163,84 | 99909,63 | |
| 419,9 | 17,8 | 17,8 | 7474,22 | 316,84 | 133041,1 | |
| 22,8 | 22,8 | 519,84 | 98769,6 | |||
| 31,8 | 31,8 | 1011,24 | 65730,6 | |||
| Итого | 4998,8 | 53868,66 | 755387,9 |
|
|
|
а) Размах вариации: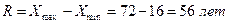 
, где 
максимальное и минимальное значение варьирующего признака;
б) Среднее линейное отклонение рассчитаем по формуле:
в) Среднее квадратическое отклонение рассчитаем по формуле:
г) Коэффициент вариации определим по следующей формуле:
.
Индивидуальные значения признака отличаются от его средней величины на 12,3 года или на 35,9%. Поскольку 
, следовательно, совокупность можно считать неоднородной.
3) Мода (Мо) – это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой.
Для определения моды в интервальных вариационных рядах с равными интервалами используют следующую формулу:
где 
- нижняя граница модального интервала;
- величина модального интервала;
- частота модального интервала;
- частота интервала, предшествующего модальному интервалу;
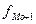- частота интервала, следующего за модальным.
Модальный интервал в интервальном ряду определяется по наибольшей частоте.
Произведем расчет: модальный интервал – 20-24, поскольку данному интервалу соответствует наибольшая частота (
);
; 
; 
; 
Подставив в формулу моды соответствующие значения, получим:
Медиана (Ме) – это значение признака, которое делит статистическую совокупность на две равные части. Медиана для интервального вариационного ряда с равными интервалами рассчитывается по следующей формуле:
где 
- нижняя граница медианного интервала;
- величина медианного интервала;
- полусумма частот ряда;
- сумма накопленных частот в интервалах, предшествующих медианному;
- частота медианного интервала.
Для определения медианного интервала необходимо рассчитать суммы накопленных частот.
| Возрастная группа, лет | Численность безработных, тыс. чел.
| Накопленная частота,
|
| До 20 | 474,9 | 474,9 |
| 20-24 | 1079,7 | 1554,6 |
| 25-29 | 694,8 | 2249,4 |
| 30-34 | 464,9 | 2714,3 |
| 35-39 | 499,9 | 3214,2 |
| 40-44 | 499,9 | 3714,1 |
| 45-49 | 609,8 | 4323,9 |
| 50-54 | 419,9 | 4743,8 |
| 55-59 | 4933,8 | |
| 60-72 | 4998,8 | |
| Итого | 4998,8 | - |
Произведем расчет:
а) определим порядковый номер медианы 
;
|
|
|
б) определим накопленную частоту медианного интервала: 
, 
;
в) определим соответствующий накопленной частоте медианный интервал: «30-34».
г) 
лет; 
=4 года; =2249,4; =464,9 тыс. чел.
д) рассчитаем значение медианы:
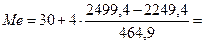32,2 года,
то есть половина безработных имеет средний возраст меньше 32,2 лет, вторая половина – больше 32,2 лет.
Задача № 3
Проведено 5-% обследование качества поступившей партии товара. Па основе механического способа отбора в выборочную совокупность взято 800 единиц, из которых 40 оказались бракованными. Средний вес одного изделия в выборке составил 10,0 кг, а среднее квадратическое отклонение - 0,25.
Определите:
1. С вероятностью 0,997 пределы, в которых находится генеральная доля бракованной продукции.
2. С вероятностью 0,954 пределы, в которых находится средний вес одного изделия во всей партии товара.
Решение:
1. Определим генеральную долю бракованной продукции:
2. Рассчитаем среднюю ошибку выборки для доли бракованной продукции:
3. Рассчитаем предельную ошибку выборки для доли бракованной продукции:
(
P=0,997)
4. Для определения интервальной оценки генеральной доли бракованной продукции воспользуемся формулой:
или 
Следовательно, с вероятностью 99,7% можно утверждать, что доля бракованной продукции находится в пределах от 2,7% до 7,3%.
5. Рассчитаем среднюю ошибку выборки для среднего веса одного изделия во всей партии товара:
0,009 кг.
6. Рассчитаем предельную ошибку выборки для среднего веса одного изделия во всей партии товара:
(
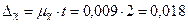
P=0,954)
7. Для определения интервальной оценки среднего веса изделия воспользуемся формулой:
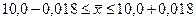
Следовательно, с вероятностью 95,4% можно утверждать, что средний вес одного изделия во всей партии товара колеблется в пределах от 9,982 кг до 10,018 кг.
|
|
|
